DDA
Traditionally, analog computers use operational amplifiers to implement addition, subtraction and to compute time-integrals of functions. Multiplication was handled by analog multipliers. All of these operations are easy to perform on the FPGA, except for computing time integrals. However, around the time that digital circuitry was getting faster then analog computation, a device called a Digital Differential Analyzer (DDA) was invented to simulate the integral function digitally. I used a version of the DDA which was easy to implement on the FPGA and which gives speedy parallel execution.
The general approach using DDAs will be to simulate a system of
first-order differential equations, which can be nonlinear. Analog
computers use operational amplifiers to do mathematical integration. We
will use digital summers and registers. For any set of differential
equations with state variables v1 to vm:
dv1/dt = f1(t,v1,v2,v3,...vm)
dv2/dt = f2(t,v1,v2,v3,...vm)
dv3/dt = f3(t,v1,v2,v3,...vm) ...dvm/dt = fm(...)
We will build the following circuitry to perform an Euler integration approximation to these equations in the form
v1(n+1) = v1(n) + dt*(f1(t,v1(n),v2(n),v3(n),...vm(n))
v2(n+1) = v2(n) + dt*(f2(t,v1(n),v2(n),v3(n),...vm(n))
v3(n+1) = v3(n) + dt*(f3(t,v1(n),v2(n),v3(n),...vm(n))
...
vm(n+1) = vm(n) + dt*(fm(...)) Where the variable values at time step n are updated to form the values at time step n+1. Each equation will require one integrator. The multiply may be replaced by a shift-right if dt is chosen to be a power of two. Most of the design complexity will be in calculating F(t,V(n)).
We also need a number representation. I chose 18-bit 2's complement with
the binary point between bits 15 and 16 (with bit zero being the least
significant). Bit 17 is the sign bit. The number range is thus -2.0 to +1.999985.
This range fits well with the Audio codec which requires 16-bit 2's
complement for output to the DAC. Conversion from the 18-bit to 16-bit
just requires truncating the least significant two bits ([1:0]). A few
numbers are shown in the table below. Note that the underscore character
in the hexidecimal form is allowed in verilog to improve readability.
Decimal number
18-bit 2's comp>representation
1.0
18'h1_0000
0.5
18'h0_8000
0.25
18'h0_4000
0
18'h0_0000
-0.25
18'h3_c000
-0.5
18'h3_8000
-1.0
18'h3_0000
-1.5
18'h2_8000
All details at
http://people.ece.cornell.edu/land/courses/ece5760/DDA/index.htm
second order system
Second order system (damped spring-mass oscillator): As an example, consider the linear, second-order differential equation resulting from a damped spring-mass system:
d2x/dt2 = -k/m*x-d/m*(dx/dt)
where k is the spring constant, d the damping coefficient, m
the mass, and x the displacement. We will simulate this by converting
the second-order system into a coupled first-order system. If we let v1=x and v2=dx/dt then the second order equation is equivalent to
dv1/dt = v2
dv2/dt = -k/m*v1-d/m*v2
These equations can be solved by wiring together two
integrators, two multipliers and an adder as shown below. In the past
this would have been done by using operational amplifiers to compute
each mathematical operation. Each integrator must be supplied with an
initial condition.
Converting this diagram to Verilog, the top-level module verilog code defines the 18-bit, signed, state variables and a clock divider variable (count).
The clocked section resets and updates the state variables. The
combinatorial statements compute the Euler approximation to the F(t,V(n)). The separate multiply module ensures that the multiplies will be instantiated as hardware multipliers. The Audio_DAC_ADC module was modifed to allow either ADC-to-DAC passthru or to connect the
computation output to the DAC, depending on the position of SW17. SW17
up connects the computation.
/state variables
reg signed [17:0] v1, v2 ;
wire signed [17:0] v1new, v2new ;
//signed mult output
wire signed [17:0] v1xK_M, v2xD_M ;
// the clock divider
reg [4:0] count;
//Update state variables of simulation of spring- mass
always @ (posedge CLOCK_50)
begin
count <= count + 1;
if (KEY[3]==0) //reset
begin
v1 <= 32'h10000 ; //
v2 <= 32'h00000 ;
//count <= 0;
end
else if (count==0)
begin
v1 <= v1new ;
v2 <= v2new ;
end
end
// Compute new F(t,v) with dt = 2>>9
// v1(n+1) = v1(n) + dt*v2(n)
assign v1new = v1 + (v2>>>9);
// v2(n+1) = v2(n) + dt*(-k/m*v1(n) - d/m*v2(n))
signed_mult K_M(v1xK_M, v1, 18'h10000);
signed_mult D_M(v2xD_M, v2, 18'h00800);
assign v2new = v2 - ((v1xK_M + v2xD_M)>>>9);
module signed_mult (out, a, b);
output [17:0] out;
input signed [17:0] a;
input signed [17:0] b;
wire signed [17:0] out;
wire signed [35:0] mult_out;
assign mult_out = a * b;
assign out = {mult_out[35], mult_out[32:16]};
endmodule Time scaling the solution requires consideration of the value of dt and the update rate (CLOCK_50/(clock divider)) of the state variables. As shown in the code, the clock divider variable (count) is 5-bits wide, so it will overflow and cause an update every 32 CLOCK_50 cycles. If the time step, dt=2-9, then 29 steps must equal one time unit. 29 steps at an update rate of 5*107/32
yields a time unit of 0.328 mSec. A k/m=1 implies a period of 6.28 time
units per cycle, so one cycle in this case would be 2.06 mSec.
corresponding to 486 Hz.
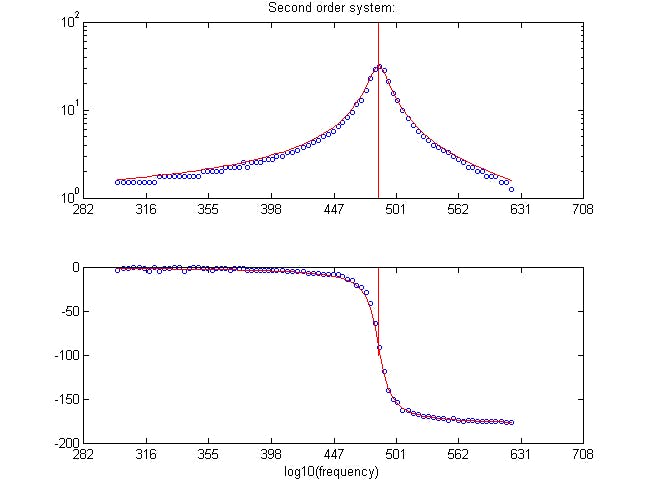
If the calculation is scaled in time to be in the audio range, then
the audio DAC may be used to watch waveforms on an oscilloscope. For the
damped spring-mass oscillator with a k/m=1, d/m=1/16, dt=2-8, and a clock rate of 5*108/64
I got the figure below. The top trace is v1 and the bottom is v2. The
frequency computed from the time scaling considerations is 486 Hz, while
the measured was 475 Hz. Reducing dt to dt=2-9
(see paragraph above) and the clock divider to 32 made the measured
frequency 486, matching the computed value. The better match with
smaller dt illustrates that the integration is approximate.
The whole project is zipped here.
The design consumed 2% of the logic resources of the FPGA, 1% of the
memory, and 4 out of 70 9-bit multipliers. You could threfore expect to
put up to 50 integrators and 35 multipilers in a bigger design.


Comments