Doing Math in FPGA

Introduction

FPGA are excellent for the implementation of Math in the programmable logic. This is due to the ability to implement parallel implementations of the algorithms. We can use maths in our FPGA to implement a range of applications from signal processing, instrumentation, image processing and control algorithms. This means FPGA are used in a range of applications from image processing in autonomous vehicles to RADAR and aircraft flight control systems.

Implementation of maths in FPGA does however take some thought, as FPGA are register rich and contain such features as dedicated multiplier accumulates (DSP48).

This makes them ideal for the implementation of fixed point maths, this is different to the floating point we tend to use and as such requires a little thought.

Fixed Point Math

A fixed-point number will have the decimal point at a fixed location in the vector. To the left of the decimal point is the integer element while the fractional element is to the right. This means that we may need to use several registers to accurately quantize the number. However, registers are normally plentiful in FPGAs.

By contrast, a floating-point number can store a much wider range than in a fixed-register width (e.g., 32-bits). The formatting of the register is split between sign, exponent, and mantissa, and the decimal point can float, thereby enabling a value far more than the 2^32-1 when used as a straight 32-bit register.

However, implementing fixed-point math in programmable logic has several advantages and is much less complex to implement. This enables a faster solution when implemented in logic since a fixed-point solution uses significantly less resources which enables easier routing and therefore increased performance.

Important to note is that there are rules and nomenclatures used when working with fixed-point math. One of the first and most important is how engineers describe the location of the decimal point within the vector. One of the most used formats is the Q format (quantized format in its long form). Q format is presented as a Qx where x is the number of fractional bits in the word. For example, Q8 would mean the decimal point is located between the 8th and 9th registers.

How we determine the number of necessary fractional elements depends on the accuracy required. For example, if we wanted to store the number 1.4530986319x10-4 using Q format, we would need to determine the number of fractional bits necessary.

If we wanted to use 16 fractional bits, we multiply the number by 63356 (2^16) and this would result in a value of 9.523023. This value can be stored easily within registers; however, its accuracy is not very good as 9/65536 = 1.37329101563x10-4 as we cannot store the fractional elements. This leads to a loss of accuracy which might impact the end results.

Instead of using 16 fractional bits, we could use 28 fractional bits which would result in the value of 39006 being stored in the fractional registers. This gives much more accurate quantized results.

With the basics of quantization understood, the next step is to understand the rules regarding the alignment of the decimal points for the mathematical operations. We will not get the correct result if we perform operations and the decimal points are not aligned.

With the basics of quantization understood, the next step is to understand the rules regarding the alignment of the decimal points for the mathematical operations. We will not get the correct result if we perform operations and the decimal points are not aligned.

• Addition – Decimal points must be aligned
• Subtraction – Decimal Points must be aligned
• Division – Decimal points must be aligned
• Multiplication – Decimal points do not need to be aligned

We also need to consider the impact of the operation on the resultant vector. Failure to consider the size of the result might result in the overflow. The table below shows the rules for the sizing of the results.

This would give in the following cases assuming we have two vectors (one 16 bit another 8 bit):

• C (16 downto 0) = A (15 downto 0) + B (7 downto 0)
• C (16 downto 0) = A (15 downto 0) - B (7 downto 0)
• C (22 downto 0) = A (15 downto 0) * B (7 downto 0)
• C (8 downto -1) = A (15 downto 0) / B (7 downto 0)

When it comes to the -1 above, this reflects an increase in the size of the register for the fractional element. Depending on which type is being used, this might be 8 downto -1 if VHDL fixed-point package is used or 9 downto 0 with Q1 otherwise.

One final note on division it can be quite resource intensive therefore it is often best if possible to use powers of two. This can be implemented as a shift, if a sift cannot be used another approach can be used of multiplying by the reciprocal, this again saves resources and eases development

Simple algorithm

Now we understand the rules of fixed point maths lets take a look at how we are able to implement a simple algorithm. In this case we are going to implement a simple rolling average function.

To get started with this application we need to first open a new Vivado project and add in two files. The first file is the source while the second is the test bench, both files should be created as VHDL2008.

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;

--library ieee_proposed;
use ieee.fixed_pkg.all;

entity math_example is port(
 clk : in std_logic;
 rst : in std_logic;
 
 ip_val : in std_logic;
 ip : in std_logic_vector(7 downto 0);
 
 op_val : out std_logic;
 op : out std_logic_vector(7 downto 0));

end math_example;

architecture Behavioral of math_example is

constant divider : ufixed(-1 downto -16):= to_ufixed( 0.1, -1,-16 ) ; 

signal accumulator : ufixed(11 downto 0) := (others => '0');
signal average : ufixed(11 downto -16 ) := (others => '0');

begin

acumm : process(rst,clk)
begin
 
 if rising_edge(clk) then 
    if rst = '1' then 
        accumulator <= (others => '0');
        average <= (others => '0');
    elsif ip_val = '1' then 
        accumulator <= resize (arg => (accumulator + to_ufixed(ip,7,0)-average(11 downto 0)), size_res => accumulator);
        average <= accumulator * divider;
    end if;
 end if;
end process;

op <= to_slv(average(7 downto 0));

end Behavioral;

The test bench looks as below

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use ieee.numeric_std.all;

entity tb_math is
--  Port ( );
end tb_math;

architecture Behavioral of tb_math is

component math_example is port(
 clk : in std_logic;
 rst : in std_logic;
 
 ip_val : in std_logic;
 ip : in std_logic_vector(7 downto 0);
 
 op_val : out std_logic;
 op : out std_logic_vector(7 downto 0));

end component math_example;

type input is array(0 to 59) of integer range 0 to 255;

signal stim_array : input := (70,71,69,67,65,68,69,66,65,72,70,69,67,65,70,64,69,65,68,64,69,70,72,68,65,72,69,67,67,68,70,71,69,67,65,68,69,66,65,72,70,69,67,65,70,64,69,65,68,64,69,70,72,68,65,72,69,67,67,68);

constant clk_period : time := 100 ns;
signal clk : std_logic := '0';
signal rst :  std_logic:='0';
signal ip_val :  std_logic :='0';
signal ip :  std_logic_vector(7 downto 0):=(others=>'0');
signal op_val :  std_logic :='0';
signal op : std_logic_vector(7 downto 0):=(others=>'0');

begin

clk_gen : clk <= not clk after (clk_period/2);

uut: math_example port map(clk, rst, ip_val, ip, op_val, op);

stim : process
begin 
 rst <= '1' ;
 wait for 1 us;
 rst <= '0';
 wait for clk_period;
 wait until rising_edge(clk);
 for i in 0 to 59 loop
  wait until rising_edge(clk);
  ip_val <= '1';
  ip <= std_logic_vector(to_unsigned(stim_array(i),8));
  wait until rising_edge(clk);
  ip_val <= '0';
 end loop;
 wait for 1 us;
 report "simulation complete" severity failure;
end process;
 

end Behavioral;

These files have leverage the VHDL 2008 fixed package which provides significant help when working with the fixed point numbers. There is also a floating point package which will also synthesis and support floating point numbers.

Lets take a look step by step at these files and what they are doing

Entity Overview*

• Clock - synchronous clock for the module
• Reset - resets the module to a known state
• Input Valid (op_val) - this indicates a new input value is available to be averaged
• Ip = 8 bit (7 downto 0) - the input average value
• Output Valid (in_val) - this indicates a new average value is available
• Op = 8 bit (7 downto 0) - the output average value

entity math_example is port(
 clk : in std_logic;
 rst : in std_logic;
 
 ip_val : in std_logic;
 ip : in std_logic_vector(7 downto 0);
 
 op_val : out std_logic;
 op : out std_logic_vector(7 downto 0));

end math_example;

The first part of our architecture is the divider which is a constant. It’s defined as unsigned fixed point type (ufixed) because we are working with unsigned numbers. This is completely fractional with no integer bits so we define it from -1 down to -16 which gives us a 16 bit number.

constant divider : ufixed(-1 downto -16):= to_ufixed( 0.1, -1,-16 ) ; 

Accuracy can be determined by

• 0.1 x 216 = 6553.6
• 6553/216 = 0.999 = 99.9% accuracy
• To_ufixed (0.1, -1, -16)
• 0.1 - value that we want to convert
• -1 - higher bounds of the array
• -16 - lower bounds of the array

Signal accumulator - stores our values

• Initialise to 0 for simulation
• Can accumulate up to 10, 8-bit values.
• If all 10 8-bit numbers are at their maximum count (max = 255) and are added together we would need a 12 bit number, so we define the ufixed as (11 downto 0).
• We are only storing integer bits, no fractional bits.

signal accumulator : ufixed(11 downto 0) := (others => '0');

Signal average - output value

• Initialise to 0 for simulation
• 12 bit number (integer number) multiplied by 0.1 (our divider number) which is down to -16. This gives us a range of 11 to -16. Remember lesson two about vector sizing when multiplying.

signal average : ufixed(11 downto -16 ) := (others => '0');

Lets look at the active code - I have a single process which has a synchronous reset. When working with AMD devices we should use a synchronous resets, if you are unsure why my blog here demonstrates the performance improvement and power savings when they are used.

If reset is active (1) then we will set everything to zero

if rising_edge(clk) then 
    if rst = '1' then 
        accumulator <= (others => '0');
        average <= (others => '0');

If reset is not active, then on the rising edge of the clock, if the input valid (ip_val) = 1, then

• We’ll take the input value (which comes in as a standard logic vector), add it to the current accumulator value
• To_ufixed (ip, 7, 0) - VHDL will convert the value from the standard logic vector to the unsigned fixed point
• Then, because it’s a rolling average, we’ll subtract the previous average from the accumulator
• We use a resize operator because the result needs to be the same size as the accumulator (in this case, 12-bits)

elsif ip_val = '1' then 
        accumulator <= resize (arg => (accumulator + to_ufixed(ip,7,0)-average(11 downto 0)), size_res => accumulator);

After we’ve done the accumulation, we take the value of the accumulator and multiply it by the divider

average <= accumulator * divider;

Finally we output the resultant scaled average

op <= to_slv(average(7 downto 0));

The test bench applies a number of values each one varying slightly as would be the case in a noisy system.

This shows how we can implement a simple system which uses, addition, subtraction, and Multiplication in the place of division using the VHDL fixed packages.

However we might face more complicated solutions which need to be implemented in out FPGA.

Complex Algorithms

More complex algorithms can be challenging, take for example the Callendar-Van Dusen equation which is used to convert from PRT resistance to a temperature

With the exception of the Square Root we know how to implement all of the required functionality. The Square Root we can implement using a CORDIC algorithm.

However, it would be complex to implement and time consuming in verification to catch all of the corner cases.

There is a better approach we can take using polynomial approximation, if we plot the equation across the range of temperatures which are of interest.

We can extract a trend line from this plot

It is much easier to implement this polynomial equation in a FPGA than it is the implement the complex equation shown above.

The first thing we need to do is quantise the parameters such that we are able to maintain the accuracy. For this I used an Excel spreadsheet which is attached at the bottom.

Once we have worked out the quantisation we can use the fixed point packages to implement the algorithm. This time we will be working with signed numbers which are represented as twos compliment.

The complete implementation looks as below

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;

use ieee.fixed_pkg.all;

entity complex_example is port(

clk : in std_logic; 

ip_val : in std_logic;
ip     : in std_logic_vector(7 downto 0);
op_val : out std_logic;
op     : out std_logic_vector(8 downto 0));

end complex_example;

architecture Behavioral of complex_example is

type fsm is (idle, powers, sum, result);

signal current_state : fsm := idle;
signal power_a : sfixed(35 downto 0):=(others=>'0');
signal power_b : sfixed(26 downto 0):=(others=>'0');
signal power_c : sfixed(17 downto 0):=(others=>'0');

signal calc  : sfixed(49 downto -32) :=(others=>'0');
signal store : sfixed(8 downto 0) := (others =>'0');

constant a : sfixed(9 downto -32):= to_sfixed( 2.00E-09, 9,-32 ); 
constant b : sfixed(9 downto -32):= to_sfixed( 4.00E-07, 9,-32 );
constant c : sfixed(9 downto -32):= to_sfixed( 0.0011, 9,-32 ); 
constant d : sfixed(9 downto -32):= to_sfixed( 2.403, 9,-32 ); 
constant e : sfixed(9 downto -32):= to_sfixed( 251.26, 9,-32 ); 

begin

cvd : process(clk)
begin 
 if rising_edge(clk) then 
  op_val <='0';
  case current_state is 
   when idle => 
    if ip_val = '1' then 
     store <= to_sfixed('0'&ip,store);
     current_state <= powers;
    end if;
   when powers =>
    power_a <= store * store * store * store;
    power_b <= store * store * store;
    power_c <= store * store;
    current_state <= sum;
   when sum =>
    calc <= (power_a*a) - (power_b * b) + (power_c * c) + (store * d) - e;
    current_state <= result;
   when result =>
    current_state <= idle;
    op <= to_slv(calc(8 downto 0));
    op_val <='1';
   end case;
  end if;
end process;

end Behavioral;

Lets look at the elements of the code which implement the solution

First the Entity

• Clock (clk) - Drives the module
• Input Valid (ip_val) and Input (ip) - Indicates that we have the valid data on the 8 bit input (7 downto 0)
• Output Valid (op_val) and Output (op) - Once we’ve run our algorithm we output a 9 bit number (8 downto 0)

entity complex_example is port(

clk : in std_logic; 

ip_val : in std_logic;
ip     : in std_logic_vector(7 downto 0);
op_val : out std_logic;
op     : out std_logic_vector(8 downto 0));

end complex_example;

The next thing we did was define a new Type for the state machine, there are 4 states in the state machine

• Idle - wait for an input valid from the first state
• Powers - does the calculation of the powers
• Sum - adds all the powers together
• Result - passes the results to the downstream modules

type fsm is (idle, powers, sum, result);

After the type declarations there are the signals we use in the design these

• Calculated signals a-c when they have been raised to their respective powers in the algorithm.
• The number of bits used to store each result depends on the size of the input and the power they are raised to. The first thing which has to happen is to convert the eight bit unsigned number into a 9 bit signed number. Then for power_a the resultant vector size is the four nine bit vector multiplications, meaning a 36 bit vector. For power_b this is three nine bit vector multiplications and so on.

signal power_a : sfixed(35 downto 0):=(others=>'0');
signal power_b : sfixed(26 downto 0):=(others=>'0');
signal power_c : sfixed(17 downto 0):=(others=>'0');

Calculation result - output value -Large calculation result of 49 downto -32

Signal Store - conversion that we store our input in when converted to signed number

• What our input gets converted into.
• This is a 9 bit storage representing 8 bits plus a sign bit to make 9 bits
• Actual input can never be negative because the input represents a resistance value of between about 70 ohms and a few hundred ohms

signal calc  : sfixed(49 downto -32) :=(others=>'0');
signal store : sfixed(8 downto 0) := (others =>'0');

Constants a-e - coefficients calculated previously using Callendar-Van Dusen equation in excel

• The first value in to_sfixed is the value from the spreadsheet
• The second value is the number of integer bits we are storing the value in. In this case it is 9 bits because the constant needs to go up to a value of 251.26
• The third value is the number of fractional bits we will be using which is -32 and is determined by the lowest constant value of 2.00E-09. Defining the number of fractional bits is where we have worked out the quantization effectively

constant a : sfixed(9 downto -32):= to_sfixed( 2.00E-09, 9,-32 ); 
constant b : sfixed(9 downto -32):= to_sfixed( 4.00E-07, 9,-32 );
constant c : sfixed(9 downto -32):= to_sfixed( 0.0011, 9,-32 ); 
constant d : sfixed(9 downto -32):= to_sfixed( 2.403, 9,-32 ); 
constant e : sfixed(9 downto -32):= to_sfixed( 251.26, 9,-32 ); 

On the rising edge of the clock the process will be executed. Op_val is a default assignment, and unless it is set to ‘1’ elsewhere in the process, it will always be a ‘0’ output. In processes, signals are assigned the last value assigned to them, default assignments make code much more readable.

Idle State - If a value comes in (ip_val) = 1, then

• We load the store register with the value and set the sign bit to 0 to indicate a positive number
• The state machine then moves to the powers state.

if ip_val = '1' then 
     store <= to_sfixed('0'&ip,store);
     current_state <= powers;
end if;

Power State - in the power state we calculate the three powers and then move to the sum state.

• Power a - multiply the stored value by itself 4 times.
• Power b - multiply the stored value by itself 3 times
• Power c - multiply the stored value by itself 2 times

when powers =>
    power_a <= store * store * store * store;
    power_b <= store * store * store;
    power_c <= store * store;
    current_state <= sum;

Sum State - This is where we input all our values into the polynomial approximation from our excel chart and do the adding and subtracting to achieve our resulting output value.

• Note that our constants defined above have the decimal points aligned at the -32 bit no matter how big our numbers get which is important for calculating our sum since we’ll be adding and subtracting our vectors.

 calc <= (power_a*a) - (power_b * b) + (power_c * c) + (store * d) - e;
 current_state <= result;

Results State - Here we take the final value (and put it in our output as a standard logic vector. Op_val is asserted to indicate a new output value is present.

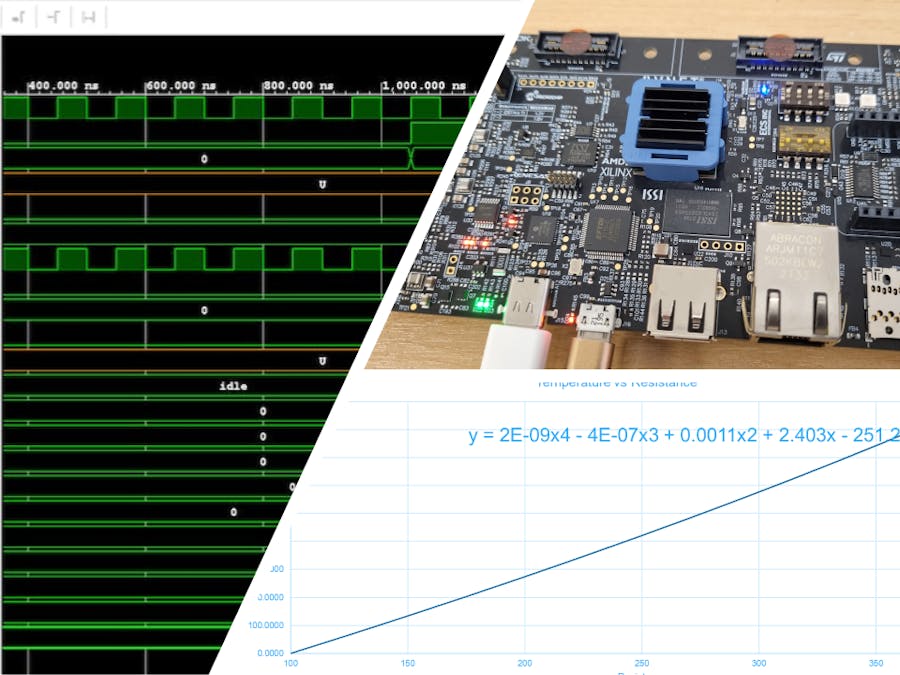
Running this code against the test bench below demonstrates the algorithm as expected.

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;

use IEEE.NUMERIC_STD.ALL;


entity tb_complex is
--  Port ( );
end tb_complex;

architecture Behavioral of tb_complex is

component complex_example is port(
clk    : in std_logic; 
ip_val : in std_logic;
ip     : in std_logic_vector(7 downto 0);
op_val : out std_logic;
op     : out std_logic_vector(8 downto 0));
end component complex_example;


signal clk    :  std_logic:='0'; 
signal ip_val :  std_logic:='0';
signal ip     :  std_logic_vector(7 downto 0):=(others=>'0');
signal op     :  std_logic_vector(8 downto 0):=(others=>'0');
signal op_val :  std_logic:='0';
constant clk_period : time := 100 ns;

begin

clk <= not clk after (clk_period/2);

uut: complex_example port map(clk,ip_val,ip,op_val,op);

stim : process
begin 
 wait for 1 us;
 wait until rising_edge(clk);
 ip_val <= '1';
 ip <= std_logic_vector(to_unsigned(61,8));
 wait until rising_edge(clk);
 ip_val <= '0';
 wait for 1 us;
 report " simulation complete" severity failure;
end process;


end Behavioral;

Running the simulation shows the conversion works as expected.

Conclusion

In this project we have walked through step by step how we can do maths with FPGA using VHDL 2008. From simple algorithms to complex algorithms we know how we can go about implementing mathematical algorithms in FPGAs