Published March 30, 2018 © Apache-2.0

Encode Image In Sound With Python

You can hide pictures in your favourite sound by generating custom sound spectrogram from an image in Python.

IntermediateWork in progress2 hours11,117

Things used in this project

Software apps and online services

Jupyter Notebook

I use this to organise the research, trial & errors

Story

What?

This project is about creating a sound that represents an image. As you may have guessed, an image is a 3D (or 5D if you do RGB) media : there is width, height and pixel intensity (greyscale or Red, Green and Blue), while sound is a 2D media: there is time and points.

How?

There is a neat tool called Fourier transform that can take a sound and output the list of frequencies that makes its wave along with their intensity. It can do that at any point in time so to make a graph called a spectrogram, which for music looks like this:

Example of sound's spectrogram

But as I was doing spectrogram analysis for a class assignment (identifying bird's sound signatures using their spectrogram), I thought it might be possible to reverse engineer the spectrogram to draw things on it, and from there get a sound wave, effectively converting images to sound

How to do it?

So to actually create the sound wave matching a particular spectrogram, all we need to do is sum a bunch of cosine waves of chosen frequency, easy. Our X axis in the image will translate to a frequency while our Y axis will be the time. Finally, the blue/red gradient is determined by the amplitude of the wave which will match the pixel intensity at that point of the image. And so we just created 3 dimensions out of a 2 dimensional object (sound wave).

The working code and further detailed explanations are available on the HTML export of the Jupyter notebook (in the attachments).

End result

import wave, struct, math # To calculate the WAV file content
import numpy as np # To handle matrices
from PIL import Image # To open the input image and convert it to grayscale

import scipy.ndimage # To resample using nearest neighbour

'''
    Loads a picture, converts it to greyscale, then to numpy array, normalise it so that the max value is 1 
    the min is 0, increase the contrast a bit, remove every pixel which intensity is lower that 0.5, 
    then resize the picture using nearest neighbour resampling and outputs the numpy matrix.
    
    FYI: imgArr[0,0] is the top left corner of the image, cheers matrix indexing
    
    Returns: the resized image as a high contrast, normalised between 0 and 1, numpy matrix
'''
def loadPicture(size, file, contrast=True, highpass=False, verbose=1):
    img = Image.open(file)
    img = img.convert("L")
    #img = img.resize(size) # DO NOT DO THAT OR THE PC WILL CRASH
    
    imgArr = np.array(img)
    imgArr = np.flip(imgArr, axis=0)
    if verbose:
        print("Image original size: ", imgArr.shape)
        
    # Increase the contrast of the image
    if contrast:
        imgArr = 1/(imgArr+10**15.2) # Now only god knows how this works but it does
    else:
        imgArr = 1 - imgArr
    # Scale between 0 and 1
    imgArr -= np.min(imgArr)
    imgArr = imgArr/np.max(imgArr)
    # Remove low pixel values (highpass filter)
    if highpass:
        removeLowValues = np.vectorize(lambda x: x if x > 0.5 else 0, otypes=[np.float])
        imgArr = removeLowValues(imgArr)

    if size[0] == 0:
        size = imgArr.shape[0], size[1]
    if size[1] == 0:
        size = size[0], imgArr.shape[1]
    resamplingFactor = size[0]/imgArr.shape[0], size[1]/imgArr.shape[1]
    if resamplingFactor[0] == 0:
        resamplingFactor = 1, resamplingFactor[1]
    if resamplingFactor[1] == 0:
        resamplingFactor = resamplingFactor[0], 1
    
    # Order : 0=nearestNeighbour, 1:bilinear, 2:cubic etc...
    imgArr = scipy.ndimage.zoom(imgArr, resamplingFactor, order=0)
    
    if verbose:
        print("Resampling factor", resamplingFactor)
        print("Image resized :", imgArr.shape)
        print("Max intensity: ", np.max(imgArr))
        print("Min intensity: ", np.min(imgArr))
    return imgArr

def genSoundFromImage(file, output="sound.wav", duration=5.0, sampleRate=44100.0, intensityFactor=1, min_freq=0, max_freq=22000, invert=False, contrast=True, highpass=True, verbose=False):
    wavef = wave.open(output,'w')
    wavef.setnchannels(1) # mono
    wavef.setsampwidth(2) 
    wavef.setframerate(sampleRate)
    
    max_frame = int(duration * sampleRate)
    max_intensity = 32767 # Defined by WAV
    
    stepSize = 400 # Hz, each pixel's portion of the spectrum
    steppingSpectrum = int((max_freq-min_freq)/stepSize)
    
    imgMat = loadPicture(size=(steppingSpectrum, max_frame), file=file, contrast=contrast, highpass=highpass, verbose=verbose)
    if invert:
        imgMat = 1 - imgMat
    imgMat *= intensityFactor # To lower/increase the image overall intensity
    imgMat *= max_intensity # To scale it to max WAV audio intensity
    if verbose:
        print("Input: ", file)
        print("Duration (in seconds): ", duration)
        print("Sample rate: ", sampleRate)
        print("Computing each soundframe sum value..")
    for frame in range(max_frame):
        if frame % 60 == 0: # Only print once in a while
            print("Progress: ==> {:.2%}".format(frame/max_frame), end="\r")
        signalValue, count = 0, 0
        for step in range(steppingSpectrum):
            intensity = imgMat[step, frame]
            if intensity < 0.1*intensityFactor:
                continue
            # nextFreq is less than currentFreq
            currentFreq = (step * stepSize) + min_freq
            nextFreq = ((step+1) * stepSize) + min_freq
            if nextFreq - min_freq > max_freq: # If we're at the end of the spectrum
                nextFreq = max_freq
            for freq in range(currentFreq, nextFreq, 1000): # substep of 1000 Hz is good
                signalValue += intensity*math.cos(freq * 2 * math.pi * float(frame) / float(sampleRate))
                count += 1
        if count == 0: count = 1
        signalValue /= count
        
        data = struct.pack('<h', int(signalValue))
        wavef.writeframesraw( data )
        
    wavef.writeframes(''.encode())
    wavef.close()
    print("\nProgress: ==> 100%")
    if verbose:
        print("Output: ", output)

import sys
import argparse

def main(argv):
    parser = argparse.ArgumentParser()
    parser.add_argument("inputImage", help="Input image in any PIL supported format (JPG, PNG (with and without alpha), BMP etc...)")
    parser.add_argument("outputFile", help="path where to output the soundfile in WAV format")
    parser.add_argument("-d", "--duration", help="Duration of the sound to output, in whole seconds, default: 5", type=int)
    parser.add_argument("-n", "--minFreq", help="Minimum frequency to use, in Hz, default: 0", type=int)
    parser.add_argument("-x", "--maxFreq", help="Maximum frequency to use, in Hz, default: 22000", type=int)
    parser.add_argument("-s", "--samplerate", help="Sample rate of the sound to output, in Hertz, default: 44100", type=int)
    parser.add_argument("-if", "--intensityFactor", help="Factory by which multiply the image intensity, in decimal, default: 1.0", type=float)
    parser.add_argument("-i", "--invert", help="Invert the image intensity, resulting in an inverted spectrum", action="store_true")
    parser.add_argument("-c", "--contrast", help="Increases image's contrast before converting it, can enhance the resulting spectrum", action="store_true")
    parser.add_argument("-hi", "--highintensity", help="Cut low intensity pixels, can enhance result", action="store_true")
    parser.add_argument("-v", "--verbose", help="Display verbose", action="store_true")
    args = parser.parse_args()
    
    img = args.inputImage
    output = args.outputFile
    duration = 5 if not args.duration else args.duration
    min_freq = 0 if not args.minFreq else args.minFreq
    max_freq = 22000 if not args.maxFreq else args.maxFreq
    sampleRate = 44100 if not args.samplerate else args.samplerate
    intensityFactor = 1 if not args.intensityFactor else args.intensityFactor
    invert = args.invert
    contrast = args.contrast
    highpass = args.highintensity # Not a real highpass, but it cuts low intensities...
    verbose = args.verbose

    genSoundFromImage(
            file=img, 
            output=output, 
            duration=duration, 
            sampleRate=sampleRate,
            min_freq=min_freq,
            max_freq=max_freq,
            contrast=contrast, 
            invert=invert, 
            intensityFactor=intensityFactor,
            highpass=highpass, 
            verbose=verbose)

if __name__ == "__main__":
    main(sys.argv[1:])

<!DOCTYPE html>
<html>
<head><meta charset="utf-8" />
<title>Spectro Gen V3</title><script src="https://cdnjs.cloudflare.com/ajax/libs/require.js/2.1.10/require.min.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/jquery/2.0.3/jquery.min.js"></script>

<style type="text/css">
    /*!
*
* Twitter Bootstrap
*
*/
/*!
 * Bootstrap v3.3.7 (http://getbootstrap.com)
 * Copyright 2011-2016 Twitter, Inc.
 * Licensed under MIT (https://github.com/twbs/bootstrap/blob/master/LICENSE)
 */
/*! normalize.css v3.0.3 | MIT License | github.com/necolas/normalize.css */
html {
  font-family: sans-serif;
  -ms-text-size-adjust: 100%;
  -webkit-text-size-adjust: 100%;
}
body {
  margin: 0;
}
article,
aside,
details,
figcaption,
figure,
footer,
header,
hgroup,
main,
menu,
nav,
section,
summary {
  display: block;
}
audio,
canvas,
progress,
video {
  display: inline-block;
  vertical-align: baseline;
}
audio:not([controls]) {
  display: none;
  height: 0;
}
[hidden],
template {
  display: none;
}
a {
  background-color: transparent;
}
a:active,
a:hover {
  outline: 0;
}
abbr[title] {
  border-bottom: 1px dotted;
}
b,
strong {
  font-weight: bold;
}
dfn {
  font-style: italic;
}
h1 {
  font-size: 2em;
  margin: 0.67em 0;
}
mark {
  background: #ff0;
  color: #000;
}
small {
  font-size: 80%;
}
sub,
sup {
  font-size: 75%;
  line-height: 0;
  position: relative;
  vertical-align: baseline;
}
sup {
  top: -0.5em;
}
sub {
  bottom: -0.25em;
}
img {
  border: 0;
}
svg:not(:root) {
  overflow: hidden;
}
figure {
  margin: 1em 40px;
}
hr {
  box-sizing: content-box;
  height: 0;
}
pre {
  overflow: auto;
}
code,
kbd,
pre,
samp {
  font-family: monospace, monospace;
  font-size: 1em;
}
button,
input,
optgroup,
select,
textarea {
  color: inherit;
  font: inherit;
  margin: 0;
}
button {
  overflow: visible;
}
button,
select {
  text-transform: none;
}
button,
html input[type="button"],
input[type="reset"],
input[type="submit"] {
  -webkit-appearance: button;
  cursor: pointer;
}
button[disabled],
html input[disabled] {
  cursor: default;
}
button::-moz-focus-inner,
input::-moz-focus-inner {
  border: 0;
  padding: 0;
}
input {
  line-height: normal;
}
input[type="checkbox"],
input[type="radio"] {
  box-sizing: border-box;
  padding: 0;
}
input[type="number"]::-webkit-inner-spin-button,
input[type="number"]::-webkit-outer-spin-button {
  height: auto;
}
input[type="search"] {
  -webkit-appearance: textfield;
  box-sizing: content-box;
}
input[type="search"]::-webkit-search-cancel-button,
input[type="search"]::-webkit-search-decoration {
  -webkit-appearance: none;
}
fieldset {
  border: 1px solid #c0c0c0;
  margin: 0 2px;
  padding: 0.35em 0.625em 0.75em;
}
legend {
  border: 0;
  padding: 0;
}
textarea {
  overflow: auto;
}
optgroup {
  font-weight: bold;
}
table {
  border-collapse: collapse;
  border-spacing: 0;
}
td,
th {
  padding: 0;
}
/*! Source: https://github.com/h5bp/html5-boilerplate/blob/master/src/css/main.css */
@media print {
  *,
  *:before,
  *:after {
    background: transparent !important;
    color: #000 !important;
    box-shadow: none !important;
    text-shadow: none !important;
  }
  a,
  a:visited {
    text-decoration: underline;
  }
  a[href]:after {
    content: " (" attr(href) ")";
  }
  abbr[title]:after {
    content: " (" attr(title) ")";
  }
  a[href^="#"]:after,
  a[href^="javascript:"]:after {
    content: "";
  }
  pre,
  blockquote {
    border: 1px solid #999;
    page-break-inside: avoid;
  }
  thead {
    display: table-header-group;
  }
  tr,
  img {
    page-break-inside: avoid;
  }
  img {
    max-width: 100% !important;
  }
  p,
  h2,
  h3 {
    orphans: 3;
    widows: 3;
  }
  h2,
  h3 {
    page-break-after: avoid;
  }
  .navbar {
    display: none;
  }
  .btn > .caret,
  .dropup > .btn > .caret {
    border-top-color: #000 !important;
  }
  .label {
    border: 1px solid #000;
  }
  .table {
    border-collapse: collapse !important;
  }
  .table td,
  .table th {
    background-color: #fff !important;
  }
  .table-bordered th,
  .table-bordered td {
    border: 1px solid #ddd !important;
  }
}
@font-face {
  font-family: 'Glyphicons Halflings';
  src: url('../components/bootstrap/fonts/glyphicons-halflings-regular.eot');
  src: url('../components/bootstrap/fonts/glyphicons-halflings-regular.eot?#iefix') format('embedded-opentype'), url('../components/bootstrap/fonts/glyphicons-halflings-regular.woff2') format('woff2'), url('../components/bootstrap/fonts/glyphicons-halflings-regular.woff') format('woff'), url('../components/bootstrap/fonts/glyphicons-halflings-regular.ttf') format('truetype'), url('../components/bootstrap/fonts/glyphicons-halflings-regular.svg#glyphicons_halflingsregular') format('svg');
}
.glyphicon {
  position: relative;
  top: 1px;
  display: inline-block;
  font-family: 'Glyphicons Halflings';
  font-style: normal;
  font-weight: normal;
  line-height: 1;
  -webkit-font-smoothing: antialiased;
  -moz-osx-font-smoothing: grayscale;
}
.glyphicon-asterisk:before {
  content: "\002a";
}
.glyphicon-plus:before {
  content: "\002b";
}
.glyphicon-euro:before,
.glyphicon-eur:before {
  content: "\20ac";
}
.glyphicon-minus:before {
  content: "\2212";
}
.glyphicon-cloud:before {
  content: "\2601";
}
.glyphicon-envelope:before {
  content: "\2709";
}
.glyphicon-pencil:before {
  content: "\270f";
}
.glyphicon-glass:before {
  content: "\e001";
}
.glyphicon-music:before {
  content: "\e002";
}
.glyphicon-search:before {
  content: "\e003";
}
.glyphicon-heart:before {
  content: "\e005";
}
.glyphicon-star:before {
  content: "\e006";
}
.glyphicon-star-empty:before {
  content: "\e007";
}
.glyphicon-user:before {
  content: "\e008";
}
.glyphicon-film:before {
  content: "\e009";
}
.glyphicon-th-large:before {
  content: "\e010";
}
.glyphicon-th:before {
  content: "\e011";
}
.glyphicon-th-list:before {
  content: "\e012";
}
.glyphicon-ok:before {
  content: "\e013";
}
.glyphicon-remove:before {
  content: "\e014";
}
.glyphicon-zoom-in:before {
  content: "\e015";
}
.glyphicon-zoom-out:before {
  content: "\e016";
}
.glyphicon-off:before {
  content: "\e017";
}
.glyphicon-signal:before {
  content: "\e018";
}
.glyphicon-cog:before {
  content: "\e019";
}
.glyphicon-trash:before {
  content: "\e020";
}
.glyphicon-home:before {
  content: "\e021";
}
.glyphicon-file:before {
  content: "\e022";
}
.glyphicon-time:before {
  content: "\e023";
}
.glyphicon-road:before {
  content: "\e024";
}
.glyphicon-download-alt:before {
  content: "\e025";
}
.glyphicon-download:before {
  content: "\e026";
}
.glyphicon-upload:before {
  content: "\e027";
}
.glyphicon-inbox:before {
  content: "\e028";
}
.glyphicon-play-circle:before {
  content: "\e029";
}
.glyphicon-repeat:before {
  content: "\e030";
}
.glyphicon-refresh:before {
  content: "\e031";
}
.glyphicon-list-alt:before {
  content: "\e032";
}
.glyphicon-lock:before {
  content: "\e033";
}
.glyphicon-flag:before {
  content: "\e034";
}
.glyphicon-headphones:before {
  content: "\e035";
}
.glyphicon-volume-off:before {
  content: "\e036";
}
.glyphicon-volume-down:before {
  content: "\e037";
}
.glyphicon-volume-up:before {
  content: "\e038";
}
.glyphicon-qrcode:before {
  content: "\e039";
}
.glyphicon-barcode:before {
  content: "\e040";
}
.glyphicon-tag:before {
  content: "\e041";
}
.glyphicon-tags:before {
  content: "\e042";
}
.glyphicon-book:before {
  content: "\e043";
}
.glyphicon-bookmark:before {
  content: "\e044";
}
.glyphicon-print:before {
  content: "\e045";
}
.glyphicon-camera:before {
  content: "\e046";
}
.glyphicon-font:before {
  content: "\e047";
}
.glyphicon-bold:before {
  content: "\e048";
}
.glyphicon-italic:before {
  content: "\e049";
}
.glyphicon-text-height:before {
  content: "\e050";
}
.glyphicon-text-width:before {
  content: "\e051";
}
.glyphicon-align-left:before {
  content: "\e052";
}
.glyphicon-align-center:before {
  content: "\e053";
}
.glyphicon-align-right:before {
  content: "\e054";
}
.glyphicon-align-justify:before {
  content: "\e055";
}
.glyphicon-list:before {
  content: "\e056";
}
.glyphicon-indent-left:before {
  content: "\e057";
}
.glyphicon-indent-right:before {
  content: "\e058";
}
.glyphicon-facetime-video:before {
  content: "\e059";
}
.glyphicon-picture:before {
  content: "\e060";
}
.glyphicon-map-marker:before {
  content: "\e062";
}
.glyphicon-adjust:before {
  content: "\e063";
}
.glyphicon-tint:before {
  content: "\e064";
}
.glyphicon-edit:before {
  content: "\e065";
}
.glyphicon-share:before {
  content: "\e066";
}
.glyphicon-check:before {
  content: "\e067";
}
.glyphicon-move:before {
  content: "\e068";
}
.glyphicon-step-backward:before {
  content: "\e069";
}
.glyphicon-fast-backward:before {
  content: "\e070";
}
.glyphicon-backward:before {
  content: "\e071";
}
.glyphicon-play:before {
  content: "\e072";
}
.glyphicon-pause:before {
  content: "\e073";
}
.glyphicon-stop:before {
  content: "\e074";
}
.glyphicon-forward:before {
  content: "\e075";
}
.glyphicon-fast-forward:before {
  content: "\e076";
}
.glyphicon-step-forward:before {
  content: "\e077";
}
.glyphicon-eject:before {
  content: "\e078";
}
.glyphicon-chevron-left:before {
  content: "\e079";
}
.glyphicon-chevron-right:before {
  content: "\e080";
}
.glyphicon-plus-sign:before {
  content: "\e081";
}
.glyphicon-minus-sign:before {
  content: "\e082";
}
.glyphicon-remove-sign:before {
  content: "\e083";
}
.glyphicon-ok-sign:before {
  content: "\e084";
}
.glyphicon-question-sign:before {
  content: "\e085";
}
.glyphicon-info-sign:before {
  content: "\e086";
}
.glyphicon-screenshot:before {
  content: "\e087";
}
.glyphicon-remove-circle:before {
  content: "\e088";
}
.glyphicon-ok-circle:before {
  content: "\e089";
}
.glyphicon-ban-circle:before {
  content: "\e090";
}
.glyphicon-arrow-left:before {
  content: "\e091";
}
.glyphicon-arrow-right:before {
  content: "\e092";
}
.glyphicon-arrow-up:before {
  content: "\e093";
}
.glyphicon-arrow-down:before {
  content: "\e094";
}
.glyphicon-share-alt:before {
  content: "\e095";
}
.glyphicon-resize-full:before {
  content: "\e096";
}
.glyphicon-resize-small:before {
  content: "\e097";
}
.glyphicon-exclamation-sign:before {
  content: "\e101";
}
.glyphicon-gift:before {
  content: "\e102";
}
.glyphicon-leaf:before {
  content: "\e103";
}
.glyphicon-fire:before {
  content: "\e104";
}
.glyphicon-eye-open:before {
  content: "\e105";
}
.glyphicon-eye-close:before {
  content: "\e106";
}
.glyphicon-warning-sign:before {
  content: "\e107";
}
.glyphicon-plane:before {
  content: "\e108";
}
.glyphicon-calendar:before {
  content: "\e109";
}
.glyphicon-random:before {
  content: "\e110";
}
.glyphicon-comment:before {
  content: "\e111";
}
.glyphicon-magnet:before {
  content: "\e112";
}
.glyphicon-chevron-up:before {
  content: "\e113";
}
.glyphicon-chevron-down:before {
  content: "\e114";
}
.glyphicon-retweet:before {
  content: "\e115";
}
.glyphicon-shopping-cart:before {
  content: "\e116";
}
.glyphicon-folder-close:before {
  content: "\e117";
}
.glyphicon-folder-open:before {
  content: "\e118";
}
.glyphicon-resize-vertical:before {
  content: "\e119";
}
.glyphicon-resize-horizontal:before {
  content: "\e120";
}
.glyphicon-hdd:before {
  content: "\e121";
}
.glyphicon-bullhorn:before {
  content: "\e122";
}
.glyphicon-bell:before {
  content: "\e123";
}
.glyphicon-certificate:before {
  content: "\e124";
}
.glyphicon-thumbs-up:before {
  content: "\e125";
}
.glyphicon-thumbs-down:before {
  content: "\e126";
}
.glyphicon-hand-right:before {
  content: "\e127";
}
.glyphicon-hand-left:before {
  content: "\e128";
}
.glyphicon-hand-up:before {
  content: "\e129";
}
.glyphicon-hand-down:before {
  content: "\e130";
}
.glyphicon-circle-arrow-right:before {
  content: "\e131";
}
.glyphicon-circle-arrow-left:before {
  content: "\e132";
}
.glyphicon-circle-arrow-up:before {
  content: "\e133";
}
.glyphicon-circle-arrow-down:before {
  content: "\e134";
}
.glyphicon-globe:before {
  content: "\e135";
}
.glyphicon-wrench:before {
  content: "\e136";
}
.glyphicon-tasks:before {
  content: "\e137";
}
.glyphicon-filter:before {
  content: "\e138";
}
.glyphicon-briefcase:before {
  content: "\e139";
}
.glyphicon-fullscreen:before {
  content: "\e140";
}
.glyphicon-dashboard:before {
  content: "\e141";
}
.glyphicon-paperclip:before {
  content: "\e142";
}
.glyphicon-heart-empty:before {
  content: "\e143";
}
.glyphicon-link:before {
  content: "\e144";
}
.glyphicon-phone:before {
  content: "\e145";
}
.glyphicon-pushpin:before {
  content: "\e146";
}
.glyphicon-usd:before {
  content: "\e148";
}
.glyphicon-gbp:before {
  content: "\e149";
}
.glyphicon-sort:before {
  content: "\e150";
}
.glyphicon-sort-by-alphabet:before {
  content: "\e151";
}
.glyphicon-sort-by-alphabet-alt:before {
  content: "\e152";
}
.glyphicon-sort-by-order:before {
  content: "\e153";
}
.glyphicon-sort-by-order-alt:before {
  content: "\e154";
}
.glyphicon-sort-by-attributes:before {
  content: "\e155";
}
.glyphicon-sort-by-attributes-alt:before {
  content: "\e156";
}
.glyphicon-unchecked:before {
  content: "\e157";
}
.glyphicon-expand:before {
  content: "\e158";
}
.glyphicon-collapse-down:before {
  content: "\e159";
}
.glyphicon-collapse-up:before {
  content: "\e160";
}
.glyphicon-log-in:before {
  content: "\e161";
}
.glyphicon-flash:before {
  content: "\e162";
}
.glyphicon-log-out:before {
  content: "\e163";
}
.glyphicon-new-window:before {
  content: "\e164";
}
.glyphicon-record:before {
  content: "\e165";
}
.glyphicon-save:before {
  content: "\e166";
}
.glyphicon-open:before {
  content: "\e167";
}
.glyphicon-saved:before {
  content: "\e168";
}
.glyphicon-import:before {
  content: "\e169";
}
.glyphicon-export:before {
  content: "\e170";
}
.glyphicon-send:before {
  content: "\e171";
}
.glyphicon-floppy-disk:before {
  content: "\e172";
}
.glyphicon-floppy-saved:before {
  content: "\e173";
}
.glyphicon-floppy-remove:before {
  content: "\e174";
}
.glyphicon-floppy-save:before {
  content: "\e175";
}
.glyphicon-floppy-open:before {
  content: "\e176";
}
.glyphicon-credit-card:before {
  content: "\e177";
}
.glyphicon-transfer:before {
  content: "\e178";
}
.glyphicon-cutlery:before {
  content: "\e179";
}
.glyphicon-header:before {
  content: "\e180";
}
.glyphicon-compressed:before {
  content: "\e181";
}
.glyphicon-earphone:before {
  content: "\e182";
}
.glyphicon-phone-alt:before {
  content: "\e183";
}
.glyphicon-tower:before {
  content: "\e184";
}
.glyphicon-stats:before {
  content: "\e185";
}
.glyphicon-sd-video:before {
  content: "\e186";
}
.glyphicon-hd-video:before {
  content: "\e187";
}
.glyphicon-subtitles:before {
  content: "\e188";
}
.glyphicon-sound-stereo:before {
  content: "\e189";
}
.glyphicon-sound-dolby:before {
  content: "\e190";
}
.glyphicon-sound-5-1:before {
  content: "\e191";
}
.glyphicon-sound-6-1:before {
  content: "\e192";
}
.glyphicon-sound-7-1:before {
  content: "\e193";
}
.glyphicon-copyright-mark:before {
  content: "\e194";
}
.glyphicon-registration-mark:before {
  content: "\e195";
}
.glyphicon-cloud-download:before {
  content: "\e197";
}
.glyphicon-cloud-upload:before {
  content: "\e198";
}
.glyphicon-tree-conifer:before {
  content: "\e199";
}
.glyphicon-tree-deciduous:before {
  content: "\e200";
}
.glyphicon-cd:before {
  content: "\e201";
}
.glyphicon-save-file:before {
  content: "\e202";
}
.glyphicon-open-file:before {
  content: "\e203";
}
.glyphicon-level-up:before {
  content: "\e204";
}
.glyphicon-copy:before {
  content: "\e205";
}
.glyphicon-paste:before {
  content: "\e206";
}
.glyphicon-alert:before {
  content: "\e209";
}
.glyphicon-equalizer:before {
  content: "\e210";
}
.glyphicon-king:before {
  content: "\e211";
}
.glyphicon-queen:before {
  content: "\e212";
}
.glyphicon-pawn:before {
  content: "\e213";
}
.glyphicon-bishop:before {
  content: "\e214";
}
.glyphicon-knight:before {
  content: "\e215";
}
.glyphicon-baby-formula:before {
  content: "\e216";
}
.glyphicon-tent:before {
  content: "\26fa";
}
.glyphicon-blackboard:before {
  content: "\e218";
}
.glyphicon-bed:before {
  content: "\e219";
}
.glyphicon-apple:before {
  content: "\f8ff";
}
.glyphicon-erase:before {
  content: "\e221";
}
.glyphicon-hourglass:before {
  content: "\231b";
}
.glyphicon-lamp:before {
  content: "\e223";
}
.glyphicon-duplicate:before {
  content: "\e224";
}
.glyphicon-piggy-bank:before {
  content: "\e225";
}
.glyphicon-scissors:before {
  content: "\e226";
}
.glyphicon-bitcoin:before {
  content: "\e227";
}
.glyphicon-btc:before {
  content: "\e227";
}
.glyphicon-xbt:before {
  content: "\e227";
}
.glyphicon-yen:before {
  content: "\00a5";
}
.glyphicon-jpy:before {
  content: "\00a5";
}
.glyphicon-ruble:before {
  content: "\20bd";
}
.glyphicon-rub:before {
  content: "\20bd";
}
.glyphicon-scale:before {
  content: "\e230";
}
.glyphicon-ice-lolly:before {
  content: "\e231";
}
.glyphicon-ice-lolly-tasted:before {
  content: "\e232";
}
.glyphicon-education:before {
  content: "\e233";
}
.glyphicon-option-horizontal:before {
  content: "\e234";
}
.glyphicon-option-vertical:before {
  content: "\e235";
}
.glyphicon-menu-hamburger:before {
  content: "\e236";
}
.glyphicon-modal-window:before {
  content: "\e237";
}
...

This file has been truncated, please download it to see its full contents.

{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Spectrogram Generator\n",
    "_By Sam_\n",
    "\n",
    "This project is about creating a sound that represents an image. As you may have guessed, an image is a 3D (or 5D if you do RGB) media : there is width, height and pixel intensity (greyscale or Red, Green and Blue), while sound is a 2D media: there is time and points.\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 250,
   "metadata": {},
   "outputs": [],
   "source": [
    "import wave, struct, math # To calculate the WAV file content\n",
    "import numpy as np # To handle matrices\n",
    "from PIL import Image # To open the input image and convert it to grayscale\n",
    "\n",
    "import scipy                     # To plot the spectrogram\n",
    "import matplotlib.pyplot as plt  # To plot the spectrogram\n",
    "import scipy.io.wavfile          # To plot the spectrogram\n",
    "\n",
    "import scipy.ndimage # To resample using nearest neighbour\n",
    "import IPython.display  # Jupyter notebook ..."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Plotting\n",
    "These two functions allows me to plot data\n",
    "\n",
    " - `plotSpectrogram` \n",
    " \n",
    " Plots the spectrogram (frequencies and their intensity along time axis) of a given WAVE file. Also display its name and sample rate\n",
    " \n",
    " \n",
    " - `plotMat` \n",
    " \n",
    " Plots a matrix (2D tensor) in the common representation (i=0,j=0 on the top left corner). The values are represented by colour intensity"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 251,
   "metadata": {},
   "outputs": [],
   "source": [
    "def plotSpectrogram(file=\"sound.wav\"):\n",
    "    sample_rate, X = scipy.io.wavfile.read(file)\n",
    "    plt.specgram(X, Fs=sample_rate, xextent=(0,60))\n",
    "    print(\"File: \", file)\n",
    "    print(\"Sample rate (Hz): \",sample_rate)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 252,
   "metadata": {},
   "outputs": [],
   "source": [
    "def plotMat(mat):\n",
    "    mat = np.flip(mat,0)\n",
    "    X, Y = np.meshgrid(range(mat.shape[0]), range(mat.shape[1]))\n",
    "    Z = mat[X,Y]\n",
    "\n",
    "    plt.pcolormesh(Y,X,Z)\n",
    "    plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Load Picture\n",
    "The `loadPicture` function first load and converts the picture to grayscale using PIL. Then, it converts the picture into a NumPy array and perform multiple operations on its values to increase the contrast.\n",
    "\n",
    "Then, the function performs a nearest neighbour resampling of the image.\n",
    "\n",
    "\n",
    "Example of resampling:\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 253,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Original array\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "array([[0, 1, 2],\n",
       "       [3, 4, 5],\n",
       "       [6, 7, 8]])"
      ]
     },
     "execution_count": 253,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "x = np.arange(9).reshape(3,3)\n",
    "print(\"Original array\")\n",
    "x"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 254,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "After resampling by factor of 2 along both axis, using nearest neighbour\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "array([[0, 0, 1, 1, 2, 2],\n",
       "       [0, 0, 1, 1, 2, 2],\n",
       "       [3, 3, 4, 4, 5, 5],\n",
       "       [3, 3, 4, 4, 5, 5],\n",
       "       [6, 6, 7, 7, 8, 8],\n",
       "       [6, 6, 7, 7, 8, 8]])"
      ]
     },
     "execution_count": 254,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "print(\"After resampling by factor of 2 along both axis, using nearest neighbour\")\n",
    "scipy.ndimage.zoom(x, 2, order=0)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "The resampling is conducted using a factor computed such that the end size of the matrix is equal to the `size` parameter. The resampling factor can be a floating point number.\n",
    "\n",
    "Finally, `loadPicture` returns the loaded and resampled image as a NumPy array of size `size`."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 255,
   "metadata": {},
   "outputs": [],
   "source": [
    "'''\n",
    "    Loads a picture, converts it to greyscale, then to numpy array, normalise it so that the max value is 1 \n",
    "    the min is 0, increase the contrast a bit, remove every pixel which intensity is lower that 0.5, \n",
    "    then resize the picture using nearest neighbour resampling and outputs the numpy matrix.\n",
    "    \n",
    "    FYI: imgArr[0,0] is the top left corner of the image, cheers matrix indexing\n",
    "    \n",
    "    Returns: the resized image as a high contrast, normalised between 0 and 1, numpy matrix\n",
    "'''\n",
    "def loadPicture(size, file, verbose=1):\n",
    "    img = Image.open(file)\n",
    "    img = img.convert(\"L\")\n",
    "    #img = img.resize(size) # DO NOT DO THAT OR THE PC WILL CRASH\n",
    "    \n",
    "    imgArr = np.array(img)\n",
    "    if verbose:\n",
    "        print(\"Image original size: \", imgArr.shape)\n",
    "        \n",
    "    # Increase the contrast of the image\n",
    "    imgArr = imgArr/np.max(imgArr)\n",
    "    imgArr = 1/(imgArr+10**15.2)\n",
    "    \n",
    "    # Scale between 0 and 1\n",
    "    imgArr -= np.min(imgArr)\n",
    "    imgArr = imgArr/np.max(imgArr)\n",
    "    \n",
    "    # Remove low pixel values\n",
    "    removeLowValues = np.vectorize(lambda x: x if x > 0.5 else 0, otypes=[np.float])\n",
    "    imgArr = removeLowValues(imgArr)\n",
    "    \n",
    "    if size[0] == 0:\n",
    "        size = imgArr.shape[0], size[1]\n",
    "    if size[1] == 0:\n",
    "        size = size[0], imgArr.shape[1]\n",
    "    resamplingFactor = size[0]/imgArr.shape[0], size[1]/imgArr.shape[1]\n",
    "    if resamplingFactor[0] == 0:\n",
    "        resamplingFactor = 1, resamplingFactor[1]\n",
    "    if resamplingFactor[1] == 0:\n",
    "        resamplingFactor = resamplingFactor[0], 1\n",
    "    \n",
    "    # Order : 0=nearestNeighbour, 1:bilinear, 2:cubic etc...\n",
    "    imgArr = scipy.ndimage.zoom(imgArr, resamplingFactor, order=0)\n",
    "    \n",
    "    if verbose:\n",
    "        print(\"Resampling factor\", resamplingFactor)\n",
    "        print(\"Image resized :\", imgArr.shape)\n",
    "        print(\"Max intensity: \", np.max(imgArr))\n",
    "        print(\"Min intensity: \", np.min(imgArr))\n",
    "        plotMat(imgArr)\n",
    "    return imgArr"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "For this demonstration we're gonna convert this painting named _Wanderer above the Sea of Fog_ by Caspar David Friedrich:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 274,
   "metadata": {
    "scrolled": false
   },
   "outputs": [
    {
     "data": {
      "image/jpeg": "/9j/4AAQSkZJRgABAQEASABIAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wgARCAF+ASwDAREAAhEBAxEB/8QAHAAAAgIDAQEAAAAAAAAAAAAAAgMBBAAFBgcI/8QAGgEAAwEBAQEAAAAAAAAAAAAAAAECAwQFBv/aAAwDAQACEAMQAAAB5/PK4iyObUZ1TqbMV0E6OAGXJtNzq6jqMtXXOk0m/nev0z1rAAEGxktYVQEL0vay4tX5rTXFSprEpaW0oSKTWJxraFWWibVnW7zps1dam1rQeU9AhbTaCKnXNULlTNYiyPcqjhgF+K01xdi+ow1q7Z6PfLWNV2W4eyT0umWquQqbrNbm9pqOitlnRw+vw3Q41Ok0mUw7bj6I1mlpCWoZpNI1YthnarIhJ0W2ixDY5VYmipKcyN6KNpNLGiorOddUVGhuUtTlRhuFXoWG68K120ULjRBucNbqa7FaZ0rTk0CmKa27MXRSapaQxU5BAaa6kh1AW1FIRQGwbhFQm0NbSybZTUbyL2U1rBJqUta0NhFxaUyxIaeMrtOigGxF1OkJbaxbHO9tjpR0isBS9X0ZVNIClDRMBNUhBsRmKINzojioYkVdgOUS2qtljo8da5TU2ZpstGkihY0NYGKpzdma2c1rNI1zQyJCaUWk3MMhJAYwBFSImCeldkmLIA5cy7uGliaW3T0zrXNqaeOEjYyWCde1fyvW6RRQnO2qokrsAWJuay1DSkC0LU3IiZaGpkOhoYJAMlsTYqVIpiEYM07sWxAji0hJTADIapcZWOWiaQBNLJAAxZol1IIKlFpdzDk6mWSjoLlwSyRsh4nWlwNaYSzzt+Oj04AaSxVmV3KqSKS01sJpgimslzFSg6WJqQNIrQXOVM6RlSQdhNyCgyaiGCFxcQwQobW5AwFoalLVdFa0qkkSxCmaogmGEvE5TJoZeMXLc0LTdJnSUCm49CHlIAWqwFgjOq8sJaUzZIQwBZSXLUC6FCUgQhMBQMJMoGWwJRCctYxsh0naTFIGpD0fOjoEJGlNLmrAlVDEy1saxkMJrAjNpTXFAJOiRUopRciwIZImKOXk0QTcwMwhyzSW0paUzuUGyAkFpqClmxQJScqkH6IpaszBrlwCWKqVpkhQxqRoBGQxVYiEYB0pl4gqTNJNjWmNdT1ZnUywIcJql1MaihM1XRqtZRcdDnbEwzoIYguWtFRgAqkVBXMS1yxippYgQlMkGgqTKUMsXLdJ6fXM7kZpWdDmxCvFqQkeo6M9PtnR0g6Okx16HnvJpEipoZEIWnFDWipLTVItPAUyBy5xMkGBWrCLtp1K3vlZqYTp8+i4prmoqp3KLSaKdIqVHXOuy5L67n0tZ2nGloWqGRaqWgGIKSFA6CxAyWokkICKLqdtqWbHfE9ViBypcUVTrKKdJSb0QxNrGkpqarI2nNrxXL0+E9+Pe5P6LzlU0OdAiABC2RpPC9/NbT3/ADbPzpcOUHSNFq1gXuzC5RgEgc2oEBWGtNVI06ty1jpBzqtSp0vPcdvnH0MvQuW/qTmb4ZphLZSW1jK1Lzv0uXGul5N+g5NQypbCoZU2AcHzj7HmdOq3yrsctd/hdJjU4TgaBw1DmAr6LRudRa2WVKzr5Z6o9Rwr3nn1sJnLmXLWAIKpcj6HMsWy59d/y7YAyaXSdHtno9I02scVvhaEQNVNTJrbxfTZadSquxW4GNDANlWTQXHl+ufims6XQMPTubT3/g6OkTGXYCJYVNToipU68VMas3qWuO2jl+jGu00DF7lhtWudcKkGgc0bUDdLujwLCe5T3sX0Ke1ytcV8e+hycjqhHgGHrfLr9Fed02YeazpNs+Z2y5fWKqKFzXpVgALUOwOwK7LfN/Q/PomWFC5aIqtUUW6qdFgUC5KWhLBoczU/LXfjqLADAke1l/VfmdNLoy0GsUXKwbLtFOkcGzzq/nd7Cy1mxctl4joItFyizRSUee+5ojSUtKhqtTafjVzmvSdU1YelqPkb1+VTIAg9e5NPJ+rP3fl19e59EUNRchwmIMRLIGKTE8amgpYyc/28/S5aGzyjJ2+fW+q67u572dUk0iyjZZVTJpard81+R9WXzb6OC2yFge18uvle+Xv/ADbev46LEoYy6qJRzjN9LykDQAioZtN1EC4wXq3Jvxuk+Z0Wube9D9ovO1c1s61ek6pu0nVqd1k7EPwn0eb527YkMAR2ZXUJ/WvLqxVy7XnDHokXQUc4n6qmNIQcgqnKlieIvcWun1nxvXPbB2+WnLRprYr3AnQaxrKW3w1ikMm4yrme/n8o6cfENWIOBY2pfUvPp1sVrU/FdM9Y3vEasfP3IN+nQd21yKWVO4Zu+fXaA61roXO0uaDahz6vyPcIOvyfoSnlGW0xH3nFtverDmOjLyMfA7IAeABge+YXuBcu1oANlXO00tcw07Fz6Hm1JruN9D7DDboZGo8A6eexpHWrREX4FoV2IY0PW+WvKOucl7/Nvl+r789fOvGW+c3mAkIDB+g4X69JXzvUaRodI1qYDtub2WmmtIZs831+enpOT33JfSbRb0Xx31c25o6Wjyo041kDxok9znXO7Rcl7CHRpeuvGcdPMbnmt1YQ1lRjEe18HT7Zk6WognndFQuLkXsZKkvVU9DrGwF1HJr6VB0XRm1ks+TKy3ui1rPEa0wLk1AjGIA17L5PWIeXely9fpgjk6eT6Mec3n3fyer3fGfh72uf2rg39549+U7J2ukbcNTcoyqvJdTTFbOXX6M9Xg90PedWWzTZi36L5Z2w1WhoZvjqu3Jtc632a6nn2olajfP3bzOnSt8n38nJ7QOdcr1ZcvtH1F896Hhvq5cV28fYcm/sHJt6Lk+wqSc4PLSIqunoN43EVZRrdoVrOxJs4aPFX6o+ceW9rNKT5LeOq5desx06DGtwVX1z2CLVTVxsMGNLjeleedvN5t2Ze4eF6Hzt9F59PSLE0SrvubT6h4NNn0xbRtELxvnc70nfj2GNEGpaoWq2kGyna19JXzno7mlVovpbvSbSKWddBvkTXn7fF2uSt6NVal6fRc128nYc16q74Lu5q9zbnQBOT6rCvqHg27WXVZoByA9OdsVSavyaPaFbQwMQ5LofnPR1tm2J2HoYM4tM2g9EM1qea/kv2MuW6cmopUNimSCzVbRA4rKlcvnTAAVlPYRp9W+H0s6c+Z6Muvw11drcw1pa3sx2rdANpU7/ACqznXPeX0npO16Mdjsj59IubiEc1+fU/jz3uQKUpwAjUK5FVqEucIWzZRpip4UrhTXa82ndXl0vNtpGXLmxc9ExAdZFLEyQqK6VzyO7YbZ2Lmy0dDJKyNhhdS5+buqfFfU5wGSYhgMmgZiE1AiYD1aiRaFhI7aDeSbtHdxXofm9OzSPtjmKXku/PFz1uWlKK9E4ugts+h5dHS9Zuue6MfMtcrU1oGcjZ510oGpGAQg0xE6dNlnSbjWaQsDBbHSMKsqvQc49O5NfVMNNnDgNVoabaPKOzm1ogC4j0vl1p6Rr2d9hqKPL9s+VudJa6XHTQK+d1XH9WMBAEVicpuTvS9ZcDSrCgDBgyTIOhzvocn0GddbhXo3JaemKqKnRnotoDM1FrZvPXzQxXpHPt1/JdjzejTbxW2nZZafIvvcvH9eSmq9RgOVCqFqUyEtoRraEUhAYBgabgwGI7DDT6h8jo470MKHRjqWruVpcmLoOXfl7XpnFvfwvJrm6fS4M6Pnf0o8p9fgrVJjwUjWDVUJAxTWAQGEoSyAgMCQsJkLp8b9l4ejxT0sOlg6WDbROt1y2WddBxdB6yvO+SL8s78jRvsdAiuP7eejpIOYAQMMDE3TaqlLkgMJQpuQgRIFiwkTQ3+WuyitZsIJcn6fyvf1h1nLtfx08k6157utTrGAc2mkJKKQORAWsDAgGqgElqQkJAQEIAwkIA05aIRDIZIaM09xk3j93541+enzz3wxVWqWFKcoE0CThjE6tQpqREMAAWDwMCAkMDAeiR4MmhCRSAjWJqJbwJD33y+jzzSuM7uYExDGkubE0DUgtuRKaMMARAAhAxCQICAQwMDAMDCAkCCAAHKnq1OCatZa1agmACiRZglgQYBDgWMEDDBKZCIDByEBAYBA0IBYmhDBQ0ZjJOAwQNED5oU0uZAGEmDUjU5gCQDDQwMDGlMlAg9MGIAggDARSBBANbJEBKppSya7gwIJVGqFysnB4EjAQsNEMgCTIHApqQVSOQRwAAIiHIsBwQBDARKmDquICAMJBgMmyKXWaBOAAWBgQyCGoTFqAIAYbJRCIAUQEBjDAgIAZAEiAEIRAEDwAID//xAAtEAACAgICAgICAgICAwADAAABAgADBBEFEhMhBhAUMRUiMkEHIxYgJDAzQv/aAAgBAQABBQKv/LxaapNTrHTUb1Mf2fF66eusHoPcNMxZuOxV1mV6AUGVY+pknbkQ+p+54YV9W4zKPFOoBpqFkfFXVVJre6/tLH2Wt6xrSfpmh/W4B6qErr3PD2hqCz/JcfivyKa+E8ZNIUtT6dgJj4z5R/ACPdQqSlysdXJ/rWXySW7DdligGyUGJ7hRWhQ2LXiDx5OE6Pg1mojxsrhd3L7tUrK6DaX4wiV4NFRyqQljLOmoq+q/2gJgmHhnMduNsoycSvwJdd7cy20KuOrXWV+qxUoWzUFcbI9XWt2LSnj7clf4u9i3FuorxzU3YCDtuvQhsAiWgR/cV9TzLHvVizq0rNSR7hHKkMux+K23pKxT6FIjMQOOpVmpqrqllgZmv3Lav6sJiYQoKqlTG7rGs/qduRG3uvFrY+NEP5JEa2WWkg7M0IX1BsR0sARjC5j22b7n63uBXYU1DVuMsNJEWs6tWLQoH8cRF4tnmFxy1y6wR17lAqR7O81pg89tFqInhMWuFNw0knRjYzPFwxPxV6/jBocIz8Npi8cGjVViWESupdsqBnZdkVzosNSmKDVDZ7LRL/E3lUw9WH9Vhu7ILm15tk2+3aFpomLT2ZMI68arCGnaIDOkbX0SdeRptoH6zykyu3vBclK239i7HYu3A7MVq3Ci76z9TtGAhCzos8c8cAME6mGomCvU6wVbKYuoKkWWWCNZP8iqmCuwz8douNPxNz8ZQFq6t3CS0l4y+/1B7hEZDpUM6kEBpozTQg78ZnRp0aBDBWZr3rUEb66RU1NhIzmFoROpiLqBjATCZ2MYsYXZR5DC7GdTPQjamxAZ3hYzRM1CphUzqZ13CsM1qbP1uKhM8Rng9CuCuNXudJ1UAwPqBoNGALCVWeRYbU2blM8kLztCQJ/UwdZ/WaWepsQdZ6h1DqaE6zqIFnWet6EChY0/3NQrNCaEYAD1BrWhPUIBnqHrtgIdQ6+us6waE7AQsJ2neB52m5ubmvWoBNTUE8YnWdNw1kTx7JrnjMKnZT119D66TrudIaRDXDXDTOmp1jCahE/X3r6K7nQzxmCmeCLjz8aHHn48C+vX1oQgQw/fXc6bgrninj9+ITwJDQk8CT8dY2MsNKiGoTxiGuCueLU8QgSddTUImp/r69z3PcH6/c9/XuMI0X9v+tEQbgnuEtOxnYwvO0O51EKoIVSeJYUWdFmh9dJ1nX2EE6CdIEgWBZ451UQD1qa+2E9TQjpN9Rk8klMr5pN12C4FIVmofomNGYzuZ3M2TCp11M6zUP1v69RdQsNAxV3PH9mGbhMJm450Lbdl6+8bF21LNitjckrxNWApGrjJOk6zU6bni9CmGvUInWahE1Ou5qagAnVTE1F0J3WJeDN7hlhbYaf6ZZ5QCbI1Y10M8elarQ8TGYuW+K9GZXkTW4VnUGGueOa99tTuIXELTtO0Ley03uah+te6/U36XWtATU7sIW3NAkr6dyscdgBOs/U2Nsu5VX1l1G50KlMxlHyT5JbgU3/L+Tc/EvnWRbfr0VhXc6CeKGsTxQ1y/OuN9WcUFLi6rX0O00dqDv3P7SnIquhWAa+v9kxlDQ16jVz3vr6ZIu50ja09cKz5Pw5y8VsZp8E4nzcvV2VfIZ5ISCd6nkE8vqyxlT9t10OIt/6vRhgHsfsfv1NTHz7Knr+U5Syv5hZMLn8bLAtRyubTY/YTvGbf170R79rLDfq5sgKOSyaSnKU2HNy8ZMa7lAr/AAbmsdrEfU8nvsPoe/rcsbqj1iNX/Tj7lrXtsd4bAst53Cpl3y7FSZPzC0h/leYSuM2/x2WbcQNZGzGATJLSjnM3FmL8tt3/AOSYrSvmKLD5BYpXZA1NGWUBpdiqJ8n5dOIbP5W7OeKZw/zzP45OE5zH57FKgwErBbuM24D6b+0srEty6Ejcjjop5lUmR8is638w90tymY7cnozAU7D/AB/JEbiMrtd8ftaW/HrES/hrVg4u2fx+Qkqx3YrjOI3kWJyNlco526uY3yB5VzFbsuVXYCRPlF5u5ub3AZuf8eZ/g5Jb3WB9xsmuoX85jVC/5TZLeYtvezkcixWyVEOadNk2NNW2GrjmeNxFgi8UYvEgT8ELP1GYTsJ2jV9i2MhJwq9txtTGzjKwVxEA/jqS/wDE49jfwdSFuMqE/CIm8jHXlbfLyB/X+oBOOzn47OxOW/kMXJOTbGosZrMdUZcK26V8NkWBeBef+PpB8dlPx2pIvDIsHHrBxNcXjUSfgiDHADWkwu085A5jkzi4PC/IzkNVf56ywMPXXUGEJsKDFxlMbHTThEPZZy2SuNg2v3sgmp8a+OLynx+2o0v/AMdZX5WPZx/YDjggqwEgx0SdVE6TxtPHo9dT1A07He53WbExc9cha6O4uxiq5+I1mYeNrwk4nlfHB2i4zutv9SASDYK5Xk+r+SXYv7u1IVPnP9eHYahiifqfAOSWmjlsz87P/wCN+LGNxx1O+ob/AH5QRbnV0w5EfnE/kPJue4e8Lto2bi2TVhUMwnHVNfkIPCvLfJBRfm5PfKSm7JX+NbHuxccLS69gK0ql2u1aL5Cte68YWXnEj2itPnt3fjP2Z+ofcrsZJ8a4N+cz6Kq8ZGZROc5VuMxv/J8szE5bMqmLbfl5tvyLFozv5DjbuaFza7mNeAUtXX5AB8wMN/oXblfgxE5XJIx8i57b8HGBOLclI5H5wcXJq+achn52Pm2WYR5Q9znNkPUy+Ky9KxTmGDP0MzkHM+UW+bjf97gPqbnxrGxcHj2yfVvIIKL8k3MO1dtPMnHrv5TIsXe5d6HAfI/HXkZnjTI/IOdXdZ4sPNYzBvd1yNulLqqZXK01pn8jXcmPR5b3ecnzC8bXY+xj5TVTD+VZ2I6Zoyq+R+RvSeE+SvUeU5K+3kuO5VGtuu6zIuLH5Tc72n0J+voGfFuWVeDu5R76LAWBpYsa+hFSlrtNAdq6eRRX4FXOp/jMqyrJfGtv3i4DO+PQRKsHtBxrmY2U7tkuVfj6UOP8gy143j2tLvYe8X9P++H/AO3BzH7ZVNvjbP5Nmv4zlrMbJ8rNH2qc8xfJI9D19D9ifE/+1/4uzxLw56ZWP+OcurU/FYrXhtZaOKc2JxP49d5/7h/+yjIdbsF2y8inGCDHoLBKFrA9CgFHyKyzUWLj185z38me3ZSfSzp3tOdZiUP7ehTBhvYif5YOUbF5DO8R5xxa2uxqxbbLr8O7HtCmIhtPB/G8n4+uRm1eIUh68nhPNVdw4A/ix0w+MWmWcVUz/wAcGa7haCW+PMsx+NZBxnHGs4uD2i1BJr68G7GqTrm2f/EBEXZ8cC7dNhmra411G23h/igto5fGTHqbCeiY4/8AldfJOYXUQ9W4XBbKzDhpj15J/wC7/jbgsfkV5zC/P4vFH8lxmPSUAuJltNl0/CHWrA8C171YeoxMNWXIoChKfdRFcTN0BkehaD9eUmZnJioHNtVjU+qqSBjYv5D4PEO1nG/F2ccvxa4dfA8BccqqsU1XYHnmfwLtUlNwAOpz6Hri1HIyrcenhMLkOayc2137NwvPZfG0/F/nG7uArVCKBCiqFRAfB3j0bj0dUvCVnFLWq+ICt2N44teooAiAT8lEh5DZswrHq4vjFqOZwyLVgcJbkn/x1rMTifjy4w/FSmNhuaaOITpXhdAMbqlmMSKB0GbhjJpfh8L8j5/xq4lHxrFOXz/znOw/xPfY/sHQDET458lv4TN435FjcxSe5ZV3B+ndRM26IpY450tj6lv9ze4ri3F4+Z0Xy2GNc6GvA7s9NdSDF88q4/RqwwFNWhXjf/R11OgnyXnxxSn5feqc18tuz68HmrcVzz2ccvKy7CnL/Ic/mKf+N/xqub+Z5pv5/wBn6J9RWnDczdxWV8e+UY/PJ31LLjLsrTLqyyzKXyG7rXTkM7Nf6uLbrbcCFm04fwtOq0SwLc1NAKogH1/tK/bP75bkhxeDzHMtl5bZr3OzqYLeoa8iVcoVGRkpmIBqM7WQELUvs/qb2P2BZpqr3qf4/wAvbmcJnc0lNfG3/k2G3qBf2NNuxk5iY4x+U8r2EmCpnNFRlFK6JqEe3sqp7rs7RJ5Yns/oAdZ8442/kOFsc9q4H9hzG/Xozb2JadT1pvVdTlXb/sC9a16IxegwErOD+Q24bjNOS+LkV4deXyr5FtF2RlDDGVXdd4nmJblPZ4ugbNprC56xs4lVvJFa6gr7StegUFo46KD4xj8lTlN5k1k5CBfmnA0CINEr/aH+0/S2MZsKWqBLqVFX+XuGwbXIbXfZPuL/AGnE5ViU12+RqbsSqcQ/mXHwq+rYdLp0rUZ+NXZM9jjXnl/E65gWs8oAXyVpXEznuYdFisJn564y35u8bI+SDHtwPk4Wk/LH8vJcpdyKKdTvNw+yDO5JAO8de5YJkNbiBR7WE/Won7KlXS0ocfF/Or4ThKKVxtBV9B7eobIctldmHKcddW9daq39yUP9RlAnK5vwSnn7sm88mmMvIXvj49+NyfLNlcY+NP4zItmB8SZ2zLcXDy+YXGsX/wDqCfoxXPbsWgIpra4tLR/YH2P3uK/Vu8D+sDk7sMV/KOQqOL8/5OiJ/wAl+sLmsXma3LecZvbJ5ELdXXiV1w1VIzYmzdaEgo2uBxNr2YGBVQ4qFhNdYFnHY7NXgUrBjqh+W6HNmzqX1uBdxdTyATfr9DyGD1GIjOxgH3uf6FhE8xhcmLeyz41yt+Ly3KZGPxuNg/IuLyZySHHfGttDO3kYssx6/wAjMuz8aiV81mXZK5S41VOU98u5bGx5f8w46q6nkKMimzMVR80OHl2Owab1CZv3uH+sQRj2JbZ2YZqf4z9n739DUK9Z8Y1/P/8AIedp1vM4/n78AL8spcPd+ZgI5Vajc8xuFQq3ao+lf5H8t0q2aNtgnD88/HTI+T5TW3u1xP616EEA1HiqSAoEsaddT9QCb7Ewe5/uFR9AwTiHrozuU5Y8ryX7iv8A22BPhl4/HOKpKdEhtVJzvyexMu/Nsclu01uW/wCKaC79t+y039a+v8oNQsIJv3ubm/r/AHr7UTrOuyw9+QmeUw2TyyrnLcfGq+Q5SrZa1jX5HUXWF7Q2h+521GfUBLxELw19QrerG7T3DsT9wTev/Tf1r7UTQM6ia+hD7mp+p66ohYGswCclzVGMeT558hf83U/RfUHtvLBvbWdxGm//AMIEP639dvYedpubnab9mBCSi9SSNdvQEuua5wITN+mJb63obg/X0TP9/WvX/p+pua+lHskTQ1N7+h7nTUUwzW5/uAxxqf6gHoepvR67LAD/ANf9lSYBoTRmgJ+4K4+vrcHs79QfoTU6jQ/rHPdhNRjN7+tz2YPc2Nlov7b97h9/Q/x+h7gPc+lhM1uEag/X7hP1qAfY/YXcbQIJnXR2BCfe/W4P39FSGH+LJoaiLufqGdZ+p17Qpqa1Om5rUJ+wPrRM6zUA+gv1v6/f1qMup1mp1le2Jgn/xAAmEQACAQQCAgIDAQEBAAAAAAAAARECEBIhIDEDMEFREyJhQDJx/9oACAEDAQE/ASLxZcXalFStHqQ0dEk8pJ5KmTGOCTZA0JjOhvlBAkNFOjXyO/ZiQOz407GoKdDfHQxDd1S2YsxfKbySO08GuK/g/syvSoOjInglbIkdXonjBBBF8TEVJI+E+iDEhCUmJiU0mhiRofrdpvNoFQReOEk3kVm+GJFo9D5JGiRu+yCDEggnglI6CBJjUEMxqMWYshkM2QyCCLTxngrQyGQQ7wQJGiYHWZGRM8IIvHGCOEEEWRNpRKJRrnCINGjVlwggaI5646NWg1eR85JJJvrhocGrRzkkkm8GJBiQQRePVBiQQQQQReCLwQQQQYoxRgjCkwpMEQjXKOUX37JJJ/hP8J/hJJkSaP1P1P1P1P1P1P1P1NEI0QiCEQiLQucEXdUGZPOSTJmRkSaNGraNcoI9TdoOhVEk2m+yCDExMTEgggiOcPguE8YtJPPZs2bN3kn1r0wQRZMoSjIq8zfRRUvJp9+iR1ORV/ZM20aNGvXFo4xanvEwfR46HSp9DvQ/RJkxViqJJvNpvslmTFUmZY7H5q6vkp8jeqrTbvgx2ofDJD8iPyn5HykyZmZoy5QVKOCraE8lebTFovkh+RD8j44MxZgzFmLIIZBBskkliYjQ+NDgmzqRmZmRmybTZKSCCDEl2kTNWhGKMUYogxMEiKTD+kNcujI27wYMwMDA/GKkxI4O0koUQRxgghQRarS400yrUkEEc92gg0aFUbt8CRUpplE2m6HVevrjS4tTy0ZGRkZEjqJJtTSI+YFEnRTo/wDLK0DIGjoqfJXkm0k3fokq7KT8hmKv+FQqjIQ60hOSSqrmiSRO08JG+FKGrOsTHtkEWkbm+xI+BuDsiOc8kMVmrJcIVlyavME3ffJKUYmI1HHHQrSRaF63eL0qdj75eOmHsbs0QYyYwYlKkxGoskx6J9CsrqhIrphD0PsS0Vd2VEodEWopm1XObMpS7Y6/okVpslJiYuJuqZKaCqlIop3aorRSrVd2gqqi3jrhQSNEW0MSs7QO6Hqyo0KkqojYqW9H45QqEkUoTgqeTG7IaIRhPR5aY2UKairFLEqsrKr7GTdIehkknY7TfExGjokQ3BM3mLJjbHVVGiqp1dniW5PJVsdldODsxu1eLPjJI6x1SLoZIkJSVtSZSSJkwfk+xxUL+GX2Vc09FbKNsd20Oq031Zu82RBvcDF6GLTKiISNEHQq3A3JRoyJkl3g6JJszXBiqVpK0uTdoHSdEkkknYhq6lipGiB0yPRImSVVCZNm4JJFW0ZMk6JurpfY4Y6eECs+iBUHRME2rIIItJkZMygbghtkWVLZhuCqmFym3RI+MkkmTM2Zr6IVXQ9Mkb4wU0NioF4xUodCPxFNEHl/6JfQ4uibt2ZPKSSSSlw9DJQxWkWyUtCqZMCJglE281CjIb5Kz9tH/R5HeBqLKX0KiER9FNL+Sqr6vTVj2Py/Q2336IgftojLZVVk+HwQIk6JuxReeSJ98kkkmZmTJSmVPZ8XbO7r/BHqggVCXZXXGqT5vNpuv8k8EP8AhlZ1Orh3/tgfp6s/Yve+T/29ej4Hzn/b/8QALhEAAgIBAwQCAQMEAgMAAAAAAAECERIDECETIDFBIlEEMDJAFCNhcUKBM1Jg/9oACAECAQE/Ad34289vItpTohKyzK+BFdqe7ZleyVCXdRQyitmhyozvstRMhOxx9iHyKNdiHtY5Cd8kuSpXwR/yWXtZb9CF2+WTeJdkuRRre6H5stsWyW71FHyOcTNMTPezKMTwNWYmO3LK7E12vxyLzRjsyUr8HL4MBLsk/o8o6d8mIo97K3rey97LMhy+irFwxiQzESOO7IyLY5NGaMyc/oVisbE5MSZey7VvRQ4lFFbWPUXguzjbgsRRRicDVmNDW0UcDEZCZZf6b2Y2/RyYCW3+zhGSFIzMy7MTgbLHJIjqIclY5IjNMuJlEyiZxMomUS0ZITLL7HvXY2WjKJkhSRaLRZKVGRKR8irFpGB0zGtlt/0L/W3/AELtyLLLLLLL2kNHJUipFSOdqKGcnJyOzk52tjb2syLEyy+xs5KZyc9nJyWy2c7ciT3sZyUxpmLMTEpjTKZzsmxCOTkstFosuxlFFFFFHJyWzJmbMzNmRkNll71t4LZe1mQpGRkZbWXvZZbLEzIzJTMmZM6kvoerI6sxa00dSX0KcjkRRycjsvsssssstdnO3vta5MX9lf5Mf8lL7KX/ALGK+zBfZ00YpDyLn9n9z7E9QvUK1BrVP7pWof3D5mUjJmUhSZkZmRkxJFFbtlll7LTs6JVeUUvoZyNs5KMbMEdJHTRgYv0fI+RyclM525OTkQpGW7JDY32KPFiFIfJKBiUUhxRSOC4mcTNC1Dq0dQzRkjMzLvtRdGSLrZ2Svsx4K2sTLLGrGtnIsZRiikKikUhJFFGJRQ0UeNrEMssfLHsltZe9jZkXZKP0OLlLEj+JpxNbQ6fyj4PQ2NnBwcbJEdJVyS0voccXztyfI+R8jk5Fx577L3y38Clt4+Qpryfk6l/Fb0NC24IvmhIZrJWVtbQmzkb3pGCY4Di7MXvW1bexUyonTizptGLk6I6Ko1dKuUcDRW17URXJHbVi3yeBlCg36FoM/p0dKC9dtFDimdNHTHAqtvZwX9CkyNyFGt56Cl4JxcHTLOGNbJWJUZM5HY036Oi35I6KQlXYtWJnEzRkixMsvevZ/saiOJTLaNNVHt142rMRIUWxaT9i0kjE6aMUiitrRkjIczIcIlUY2Sg0cickZsc5HUZky2ZyR1W/BlNehav2h6kGR8drWSowadMSSFtZmjMeoPVHqj1TqCky2Wz5CQqscfopryO1IUtr24E19Epu/AtSTlRlfvZci7J6mMxOzWXsyM2ZsuRyUPbgqJwKRkW34PkOI6Qj2Sk2QajOpHBa8FUcFDX0Q02VSFKzR/d26sbdkVSNV2ykUUcnJTMHR02YHTOmLTMTEoc6JStnKVo8q1tPk/yyLom3IXihyEdTGNC1fsjDN2aUKfayTpbpFPbgqzGyv0P3MjEh4JHSsjokvx+LsgrHpoxoatkYNkoqIoWaenQu58lGI+DyOJieNnEW1bTmRkZIUDEiqRdHMhElZ00ixRscF5HwhrnIir8D4IO+73+grHtl6LJSK9llvfyY7Le+aESV8ChfDJQtHhDNLx3ajoUkxyIu+3LkezR6JSryPUm38RR45Yk2e9l2+hRt2IZmkPaba4RpbWi99aefEDShNfuGKSORyocrM2SliKfBF2NWT1I3RGLnwzCkYnjuvZl0N0uTU/I54NOeTszT8bN8mkMnq4C1m/JHwfl6rhUUacnZCXNDo4LS4JIbsfnklHJlkTVnJvGBp6NfuFGiboRje1iZa8DY5Y+SWoams74NPUcma2onHgq0Q+JCaJSvbSJOlZfUliQ0UhGtoR1JZVyami4q4kpStGYroamxXQ5U+DL7Fk+T9pk2RSFtNsjbMR6nJKZHVvhEtVLwdapWS1XN8kpX7KI/GPBHzySaSMkZC1GmLWa8n4mrm2fkSw0pM/CjquXV9durpZIjD1Ix3m0QtsRhyYH7eBCRhYlRZ1OTMU6E8vBwvJIUeaKxFSRBNnTUuCGiamipcMWjFIhpxv5I0tDT0ncD879mJ+Jp46SxfazUhkqGpaT5M0yySFPmkLjbIuxbXRdnDEkxw4I6TlyLTxianLNNcihzkSt+D5No09KkYJISGvZjY9H6IxcD/ZSXjvatUzVhU2kaUJM1FSI0W7JWyMZC017K+iqLG/RyJJGLI7PT5sVJ0SdcDk/RpSUZLIW1DW9JFbIatC4PNnKEyiein8kJYo1U58IjpqKFFIpHA6LHbK4KLoRzs5ei+BLmx6b8jRgfj6krxfctrL3orsZQ1ZKkies4sjq+xSOpQuUJDKIQ+yUFRzZTsSsUTEekmdNCil+hJ+kK0KX3+g2kS1jy7Y4KQtNIlwafJkvBe+JjYoI6eXJFIzjAUrLJ6tCcpxUkaTldNd9HkSrvolGzoxY/x4n9LJf8i56fExTTiKLUbRpxfkZe9+iWolwS1SeviuB605SI6+okf1T9mpquZ+LfSRXbW9fqUa0FKDs0058IcHxYhpeiiiXCMZSOnBEoN+CSXgWl7R0JtWkdNryYn4bmvi/Av4uv/wCNn4kfZRKNmLE6dPaVLyS1m3SLT5kTl/xgaGhfymUJGrpZ+BfjR9kYqPj9Ffq6t4NRNLT6cEuzW4aaFIdsohp2smYpeN0P+a9JSds6MCqJV4I+O+9q/l25+Eaeh7l3V/PUUv8A7P3+nRRRW9d9Fb0UV3//xAA8EAABAwMCAwYEBAQFBQEAAAABAAIRAyExEBIiQVEEEyAyYXEwgZGhI0JSsTNAYsEFFCTR4VNygpLwc//aAAgBAQAGPwIQYRE2lE/fS2mUPAYQCB69V5VDXcSlyIb4JQaFOvmXlWLIZ0so8XqpPNTMBTpuUvKAxr+lvVETuhCAg1gXFhEwF6K31V/NpddNDC2uz1UAE+yG5gE8yrrhjwDiC/GO72R2eVQh4YXdmI6hQDPvpI+qjddWF0GqOZUbl5oWzn1RbzUIlth6qIV3DQYQOszdZVyuWl0YXppnwSoCDnXQfSG3qnTZRKLigBcrfU2ucU53Xloeqk39F5YUAW9VxmyNltxpayzpa6sIQMIK1yr+CwlXVirK8oDT0V7BBzzfoobjS6IiysrqSuauVZWGuVzK6aThYUu5K8KykwsBRC6FedZlSDlYV1bCvpYhZ+SvCE5GltPTSThHaJK4nfRWWFfSw0yuevQLCJGl9OIrBKmFjW69PBbw4V1hRrwiVzXTXM6RtX8PW6KldNMeLCx4MK3gtbSNemnVY8OVc+DOlly0z4MrzeHGl1b4GdOq5eDHxsfA5/Cx/KZWdfMs64+FgLCxoPFjTHgwsfAxrjXHwsrKyVcrzLzeArCwsfy+FheX7ryrAXJZV1j7ry/zJV1YF59FDmFvzUsdIWSslZWVn7LP21xpjxx4fX4kHmvZe6lhUVBtPVSLg9PgYWFgrCwsLCwsa48N7K2mPBB0nWfsrL06K3C7ofg50zrhYWFjwY1kHS4VvgmUCFIN1dxUUpB/6kKf8zUZ67lR7H2r8UPIaH8wsePCPdmGdITu8G/EQt7RY9fBgLGp2VGv9j8MqPC6ox3ExuOSiITalRu5jBuVir6ZurrCxdOM8kZRKe08j4+S3MfB/pKjvife64th+yG4925cL2lbRUG7CsfFiVaAs/RQ4h49QuLgPqqrqtRopBvEV+HTOz+s3Vbsz9tGq8y0k+b0QVxHg5LkjI5I8tC1wieatfSSQuKsB8ke7Dnn6LgZsX8T7rmuqiFIYQerSvPUHoSuF7h7lcFcn3uvxQHDnFkI3GfRAbtvupB+YWVF1lcWjKYbvqm8KXO4f0693X/1lLlvPEPmhWou4hZ9M5YdceCSQG9VG+fYSup/ZcI/9ijtqtaP6Qv4hd/3L35rOstfTPpC4qbflhXp/QLDvkF+f6IR91MK9P5hTClQCR7KN/8A7XX4nEoPCOqs4HTtfFuioQPDW7Lj/MNsfVsn/dQ5s+qwjue1vuVaX/ZRTawfKUTc+6DHVtjB+VquS/3VhHtZdV0RsSrgN915voFcyVG12mF0WF5F5V/DHyX8OF5XfJdfdSaYleRoRO75KzoVqqsZHuqzx+ZxOko6Ue0sndTcHR19FTr0D+G8WV6kD1Kg1VzefRcLIVx91xYXMry/3VwSsD5qx+iwSvKsaeZZ0e5kF+ACjTrw3ayS5d40h7OqwuayV5l51MrHzREArAVd5EbWlOPU+DtLniHVH8DhkQi1wLXCxachdo7G938LjYPQ5/8AvVZXkleT5LyLyLyrAC8yzOlhpnTyro7pKufkm8k5zz5zb0C77fILYIQ7MOFvJSpW1suKNl6qalugUAKC0yULfJHlxj++pV122hVeWtpjv/SOf9lWq8nvJ+6qdre2Klcw0/0j/lZ0wsob3hsm3qiv8vI95564VxpgkqwjSCOHkt5dZdyxh9XIw4vaMeiABlNaBLyUN2YuowrfVTMLdkqfspddSyA5H8xCbw7YePCdpIkQYQbIFJnE/wBk1jBtAEAaB9Nm8kxJwE6m4tcT0EQnVAH1hzD3SmO7RWcATuDRhqb/AKoGnG3a1s36pz+8Ja/nBiUNLuErzBZ15qdo3FEh0OVzu91NSwQIgQo7Oym/blxTCHimyOGn1VOq9oFUi4Bsn946yO2zdMq1lhGE/dcyI0lRrTdQbJqMDi85Oj3hwcYtsMqpu4ycnqgajcflTg6kwl2Nqv8Ah048reaDueVPqu57Q/h/K83THhpqB3OYC3X7s4E4CeAXU1xyfUwi99geSlgG79lBeZXm3E/puhtJn2W/8vVbQC0frCazvjUfGB/dTe/NTdMYKpdRB/hHEJtQYcJujRoHaRYuIXc1+0OrOdzPJU6Ae5jcktymdlbLjGeizJWU1m6KbfufEwOPHTlsJwjbPMFHkhHmXFd/UqdyMHhGFhHYCm/qyux0qu5z4t7YXASXNxyhFsb56hd5UugM6f8AC9P+1ZugHNynPptHeYbK3v4nG+4rmhZMVN09VUP9Rug8ckKtOzi0XTX/AFPNZyifmmuJ5eKrRzbcEIbt53UmXO/ZCyaVuAQaAnjDeSDt0+ignly0J2c5QYwd2OZQ5+qxpZXv6Jn3uuIm3VBrW/hNwh6KNIXd03ub10xhAxwr2TQ5u23mQa2HSJVNw6INAklNptpuLz+WLrZUpPY+JhwRQY1pdULuEDmqP+I9taKX4zGlk4YbGfqFZpPp1XQlSuKVZ6wCUCBhHfIHonQ3K3NuiS26nryQJKtqyy83zVds5Yf28J6qeSaG3KbUqHK7mmJDeaJfaeSa8MLnEYKs3bbCZ12odZQId3bW9V37mjdTbMwn+67T2ntNAVe7e3uy7ref7LtPZwOJ7Dt9+S7PXBkvptuOR5riMlWRJ8qiQiet0dtz+y9VJFytutrq/g2s43eic2r+YY+S3bTHVbyOE2lQ10p/BMJz3C5XdsP4jsABcbeAXmEQOiD+QTixneHr/suKmaVOlwy4c1cQFRfGZVKmMvcAqvanDiZGyeqmpXe9x/UcaVKdGvVoscdxDCu4/wAQrF1N3kqv/L7rt3ZAWltGuXM2Y2P4h++nISv7rCgBbQNvVR+b3WIHJDmV6a5nTC2v8puYReKcjkqleoeM4aFULgRT5BClF/VXYN3MwtrG5QDMlPe8bn8ioAhG2dBtG8dQthaAFTZUeJwGrsjmjO4fsuwUwC78Vsx05p/+H964dqYW1Ii3t9049AjoPVCq095TIG+mcOCLuzGSMsd5gseDzIHbborwraYXRbG3WPmriVJwgA1eWQvRYEqwuULSsaClS2mu7M/lCDiWH0jK2l4o0f0N5rfRqFp9/wB0Xuq1HmLOY5OfQrFtQXjmmU+11e82GRwgJ3aO01qdEU6ZDN7olx/4ldq30trmv2zG0xy+yfPTSFc4Q+iZ2ig8sdg/1e6tFKuM0yb++lrrbuvOFJxGVA0kyscS4tDELqrrd0Uu8qtYLrrPNQE+u72aOpTnuO4ozjogWjbPRbRP/ivM4fNEPaHITTAItLVwOgepRLzMdVU9x4fQoVGuLXC4cCuy1qxBqFsOd1Tp+3Nb7sHQq8IkLMriMLbTBPrpmyvhXWVBuSg4qAbK5tpmdXf5cy+nx7P1BdE5RrdCTAmZWzkF/sszdbhleqZYbjeeivb1aoadwao6JtFzvwOQPJQbqfz8gomPQLZR+uAuKoXQfyrc9hefVAUqAazkprv+Sm0K3PS50vf0UAKE0ZRc4pzabp22KyoBun9soRTd+dg5+qz4IUckJXRQLiUF7qemAiDoUYUSNzcXvC3VHwt8S4IFjPwz6LH2XExcPCjLiT75Qbum6FOnc/qQ3GTCysbioLLddJQ4S9x5BF9dmxp5J2xmweifVrG/IJ9QuBBs0HkqgJ3WsEfCOkq45Le7yBQ1gaJku6L8OpuPsr/RfLXKKa4WcCmvpHhPXqpqjvSfynCDQyBy0lXA2lO2WXeG0+qk3d6KDuhcgrun0RayLJtNsBClv7yoei3gA1DhcY2NUed65kfpTe983QKvQ2GGP2yEyv2d39L6ZEH38EqVcWwtrT9EDE+iM29F6z4c6P2WBvdS3tBHyCu6nV//AEb/ALJu/sBnmW1P+E49mq79ubRCzYLu1Ft3UqYkoxYlecIAfNGq+zOXqnVJdSp/dNMbo+63PUQEXbAuFgRIFzzXamAfmUEBSMeCy9Vzkps4XUL08eV017N3JO57wwj9QnCdXruLGkxYSSU4X7LVP67j6okXDrg/qU1X7WeqkX0Dd1upTQ6+3ACLWUuAn6BB1TPRTgIit2qlTcOTniUKffF/VzRICFSjUbUYeYTnbsDJwh2midteOL+pO66Y0yvVGV1WfB0+B6LsM/8AWauy9mbUsONzPXkf3WVstUp/oqclx9jaf/JDtHZuFj/qPRRKc2m2DzcUHVuNxRZ2emGNH5uqFTtdZoizZsh2XsD4BHHUb+wQugQnHdNMjyp5Y7aw4aiXmSdL+K9+q2tV9Pdf3+DRrVHbWU3byVV7S4GSba3XaqFXyQHNHRWghGBCyqvZ6B2tZYuCLqjy9xUnmrH5oXnT28E48EK3w7+C+nojddzSAYDk9VG9DonPccBEm5cZK9V/9dRGvmupyvVWH0WLq/xjdf7K41OsrKun05/EC20+H9SlHprfAWIUoDwQR/J20krh+unmKcbuJ56ZUBRoR4cr+2s/B/uraHwXOvRDXPiv47FZUctOulyrfB9VmF1Xt4L648EIeK6jCjPxc6WQnSfE7qEVn4E/zIaOev8A/8QAJhABAAICAgICAgIDAQAAAAAAAQARITFBUWFxgZGhwbHR4fDxEP/aAAgBAQABPyE2CWx8RsypRvbuUPogutubgN4OoXdzwEwiKCFmJwbaxGm+JV8/EqjR4qZpZjbSsL4PJgGR0rEYl9+WIguOILDwZgPUbVSM2Ac+5Yz/AIg/xzC4bPUxmHiUgK+yBKAOeYAzCGSLZmvMSkdYi0uWpmbuXLFz5x+TA3l6M7i9maMBDNoZELDFzebernJg4GYx/K2Ern5gLW5z7wIKJ/glQx8swIV3AK76VFpljU6FXcbDnGury4qz4IC0viUraBetTEGhhVnwCRtQubEFma8pRkexFiLO/wDkUz4Xcdzo8LK8Sh0nMCmW4koY43MWog1n76mKm57hONLAliuTzLJlx1GgwHKMU5VvwxnQOoNQofMc0ezKwt1uJMo7mYNUbI2tey2HKjca19GZTm+DEIDKvUYys8EL6jMWe87xHFtrVymJfUwdBqoiANfMfGX4iG/slwM2y5TWsDkHcxtMWRldeyKU17i7H5EeN37YNoU6n+RDNLPSmANkF46mIFwMyQfhcdKcNQeJXBEuo1CG8wMGiN1NeWR2c2vEUT5sSuZUZuKDiNHNQ4s6VMex4s3A3F1qUt/kZTLL1Gn6cwtpLxuY1LVUyrFzH5Q4l7B31LJWFjSqlzufcUDL9RSt3i8q3xOpkVLLDKvtLm0zyE44ypdL6R1wDueNcfvASXNuIw9NSsCn2rtiFZKSrEc8QxIaODiGPl2y1ADd+czUBVRCxkwrV9xLu+5bC7fUZsCCJh4uXKU61HKGHiV0BnVwBAXwy/ZK3Lqir7jnHwMbgw9kcxi4IiUjpmDbG5nplSkHdoNyHzKTJAKqERNngQmCW++BA31EVyrzHSqzxiAMfBj9HqUlXc1CutO5uABxFs0Yvw8wqDQzmZG63uH+WaRzKVpk7/tEyqXs4qXi3uYIoNedzBkJlbtj2MKld57WWXg6hlUiuniBYHhxK9MsYP1HFC/1Bqa+E0d1MucwRtZcCleYcpMofmLt3MG4yhZhZ5u6qac/LNC38xLe52RxnjY/CKlL53FTdnghyNBDMWwchZwLqVNjURQFpzmLa9zhLgV9zFRtj6OYNzw5m4ihjLqPUVHDUOEI2bh1mWKp8ylkIPHE4qH5hLgDdIZ185mWpeWr9y5cKW9xkAqS1UzN+LilfpBnUIwvlC7EQ3LB4ljbl8xfAIJd/qFzWYl1FgzANBjXqJDAqFTM3zkvqAuhG8nzM5n8QS3FPSB5Ust3KjLG7G7g3dEAwr7hywEuNFxM3+YBe6nXZBAcsVK/zEsUwnbAnT1O9ctrqDlfSpTf1OxT1EdMNiianBRYHGBfUVlmsyxP6iHqWzmU41ByzLGJr9o0eZ9RxAHMK5M6WCXAZT1qUaGEbXJLmMwL09RW8XMlJqWSoV4h4vqNtVczjRkrliDI1jsg9NEoxbH2fiJjFx7GZSADc+V6lKUvUTeCZE1K5zG3JHzhTbUsjQhfjMuyLqrIu8qvc0im/iIoo4jotc7QxP8Aoi1q4hctMxxWS20sHF+pSvxEMKYYZg3DaAHiUYMvNxDuiI5MbMHr8Q/2JUafqKUyg6leGaauVfL7iraVcf8Ag9Z+oHFTL8xAailGWD7EE+EaGuIhltFd2yxrUxh7xuUN4jgjk4lxhiPX5/qY5gFb+p5U9kt/vCMviJ2M7f5i2E/EyMwY8+4EM0zOoTB2mHjLaCTJ/c7ScK/8eMfEDN0X2ELs9ZVnDAekrDMQDmpb3xKSvmNUsEsZS1skcgfqPf8AUDWrxPZO9+5Tzjs+7EvgI2wU+YFn+c8xZsWwlq33DDhxOlKrw+aiUQus5lkcuYV7YFy/Mof4mDcqG/uVc/U5BzGSr+ZVM4he1KaSsQHU/ExAX1E0xLOmDlKJbBP0/H3G+3SCt35IjckJOeV9Q1pfUSiVBpcJOPxBcF+pn6S04hEyGolDDDMWWHkh3cbtm5junuHkkpMLA8oTwwrRsGX4YEdXFHMn/wAA8EBeWW1xn1QZR2JSANDGYkSX1Hh3VyQEczBWGKViolbzKaF+obWsaYz8xvy/MOptnlTyfqMIYdtT2z3/APgv/wBx5PygTj8ymGpyoHOGU6xHsJbOTPzGnITxLVqAwLL1Fp8y+0BLirmuJy48y4payoumyaQfMdKkCjsTBG25ephF9lKC7xCu4cmcV5jyuY7X6j218wbaQHaDe/8Awcf7geUC/KU4RgOrAMmqr8zHmfLNFkqck6VSxijmYij3KFbZc0/mZHTzLoaqmoF1U8R2xc+Yt1mo3bz3KMpf1bEXZPcOYXSp8QqSPLzfRdGD7igEMURfxKPFz5u+4By4fc6iYV5hVEMJMnVzCzhMHCGJ8SQWbv8AULM/8lFd6gtimUc73B6H5mJdTxCLCn4Nnm8TvXOY1p1Fv1Gc7lrGRljbKCD1cA5x6H08w4oOI4XxAiOGFVmZeU7mYaKWxuZ7XHJv/cS/JLwE0vzUQLXwx8olGt/ExqATDvF8w4KeU46E6lHADdssCY8ywBSwTzMnnqGjUTyIC39wGRLplmUEKjpojJZnEK4H3loPKvDpjD0Iy6XwOL9dzO0NOaeZS+YNsRt4nBRTO/6jR9NQSr+aXNo7j4OrV9SiX+tHkhzXjo8ujzUX2LYNTzUKgZjfCvnx7i0D9w1WJ9jxMdY8TyZ8zJVqnrHcxYuWWFZpufEyN2wH4YEF/CCDuH0HljDdG8n9SqCdYpKCeW6v+ZbmmOh/BMXp8sSP6Q15PJL3mhELD3kRLKbqC+wymB+4ovFmQhip7XpM4BwV/cNSXSwUz1HBYddRbiQNtZHms+EgUQ7tFxMotgOCLncXY09zGijH/MvTK6X41j4eHn3YA25nP2dTEtL4hiOK8y9858wJgDliHWu838JhbyItMdNm2gniCi1/MXp+0qYhtfKDtLPmUC/cQG/zC1B3RLAF5FwlZrwjHiX1Tn/cCsaBu+IzBeN4SmHHuPhL1ZiKUSG6iVQ9ahLhHKo8BpwQRgA7CpSyzVpUm+riy0DzERpSeLanF3RGGSHWZM2bPAfT9IQAPTErWIPUwVu9kuQduuH5glCeEpk+vKo+uoLjQ4Izb3nOE0K+l8GLSFO6mdczW4uZ/tK5dPghxd1JmClJnqola/UwtvTHcZRVaIw7njsLmvL9THgMWyvmbIuQHuKDkdZwT8yqUIg3qXwAvV1Ark8+6i6+O0haJ9qyqO6lUcIFuGolaxGOw4apefRLH3HAcjh7PhshWDksfxFzL31ERfahm3PDHGAuowihyzHYeHxBQ/lcZRL0E1pj7MNin1jHPmJLyvnUBzUvzMeAPcXGlXD7t6Y522iDDeMjzuogC1V3DNa0eY/wthfB8zqJ26nGb8kGSn1O4e6iHVL5MwMncdoT4JkaEL3WPzG7cj7mV+IoXucdxk0cesrca+aLSHCRyRauOb9qgdZxq5klJ0wDmh0I8UvVxLqEyLMJZwPMdivxADKir2n4i7wfUW2D3Cr18RQbFSeRCgvFsiZWLxabbhUQTbHAQ2SwTkSBsNTvcS5PNzPOHuXvgOiNDSmkYZdV0Zu35MRYa2wBgCLdawInIHq5cYf71CRTdw/LBDRxiVplx/v4nrrHgV/ji1+BlatMz/hG/wDNb6JVnOVGMsIy/KG+fdyj4mDtSn/KC21U046S1d+qioKt94mXEkyDzG0UufoKWVPhcDpq4FrilnNR6QnuWyLM36mXB4r0I+84vP4goHGNV4lKxqIOm1POIQ0/tMgjHgi3R5LjFbL8IbuZCutHPiEGQRjUKsd0wcUfwQUXzuJszt6w2bp+o4aIq5bVRBLGBMAcSov8QJv7cv6i7Hfd31e4CCilCfHEqzQFKN84xCtLb+ck3/2ZFzRUvx332VBCFBggq5o3uBgi0XF3zbj+kx08+4FOZTsF8QfBFwR1dnHBCYiqvtOXBqDIAuqhsppOfEy5eDB7dy1pPBPUJonAzK8dq4nOZ7qc1PmXjQ8kouFZlhwf4mR3Cvn+rl0pcjI2wO5a4hoh5mMcoW4ul6LiZYITiPAS6lSFlrpf3MkC+gX5msamxTkvNxBjha7+eZdMZUpqONuo2TjlU0V65iZ7fDR3cvk7uQfZBZGbMfuVBQelD7EYW66iuDxvX0g+mbojoQiub14hNYN17S8emXUqFjJRu/3UbazrivT/AEmTmbbnL/iKVQ8PIRdWDsIISUnIljMNtz0f3AONYAiXGYXchtme5lnxtlp2wzSaNSpshMcYc+ibHmF1MdqqCX1MDLZCnarNn8/iLUr2R1HMuubvMULpyVLvhd9S2rLlWWEANUjUCaxce6MXll4WgWLzBMobQsA0u3xEzjihSm6IevCcSsuvi+ImBb8EIDt6NQi8fEaxnw4fe4lM3g3GaRfi6oWCvJ6GI78plX1Evbl3DWJ1FRZoIbENUQ4mXP8AIYmVr34jMVZjkU550oN27dyg6sNsECA3xZYOqipXae8RW259UwxMmG9T1v8AmV5SmQ3LLsIxg9Tm/wCY7HN7mqF8VLIzpiqa4R6lMhzCa7FKE2VurIQk7g/MtQmwLhTV6ypjgL3W5WYMAoiMosZG4fD40fmKrAcuYEGpU5ZXzL2OFThndy2LxMK4YG31D1xyyXR3fMrW+SKhhzfES44vUUmAUnDEL7BV3LEi1d+4JCwgOY1vKA7S7MUtFO/W4DPCSghIdtuIf9wctlqeY5a4aKVBrzGuZm3+kHmA5TUpdgaMQIpLaw0Za8csrqE6OJmSpmzcuBaYLalLhAObm0/BL/mmF4EqyvB9xYwhtxuMq5dotHIN+1KDFmIlGa5WXDXW4rIWrqWffPEfZIM4gT+RlCAF/wCZZ4bNCGDfsQymgGwcR0GBQGjmNU3Tb5iurDCGvpPRusXBlkabNBf6gXcsEMC6wRe28YOMKtxW191CGkjh/wCi5fm8/UFoVWqI/gW+5h2WshxKrUFtCSNvMYjfKa3DfUqil6qZ9g1Ehx9R8FcILsx0q91HPMeJQdTHHRSsJicsFnl/vzAFeixdwXUzI1qdVqA/iNQiY2F/UzhBCerjf0I7GWmNVLC40YiaH3TJ4EE2UpVdplbDTzBNpUb6/wCy9Ki/LDLJUPtR7l9X1a0Jd243MDUwc4+sHHUsGp5bpdeeP44HSiFj+0ouN7mHOtgmCB7ROQQ7qV25H3psQwCxlYR13TLOXkbgoMWYQT8zFEHlsr6hdpDMsNvmXMyFKvibTbZLL9TPmngFw5tx2S76jOEJazBFVocmpYM4iomjdCdeJcZDOtSmSDlFVnxHoPEhv3N1zxXLKNT99m8YV/15Zd1GHQ2voWYmHB1bPq31Ci9vX2H7n5k0JuALjQlEFDKDZvvOI8cwkq3VkVxNhzMe8+5UBOdLPMZKyxkIpd+O0Adn8Qs1ZqjmBNw+5qcOxhgX+0TIW5gFMIrlpzZGALB1KUiEO4i2YuinjUENg01MWDFEEVzK1omK+IIGNcTdqXB/YymXc5NEWj+W8/GpZOKFFTXTTvmKyyxFHRFink/bf3FFFrklhwBevzCiQEtRi4FJPC5Tu96Z6qCF1vD5jV/FwCytWkXA5MP1/Uz0L1+FQARwDgcg5P8AfMX+58OnZ/EplcO1glHS9iLBeROpQZyqvuPi13LL04WeeUusrTUv1x2xNXTEKK/WClhF8QzAAPzDaJa/LGKKO5TxvwRMOLNyp2Ip60oCUyeXX+9XFWXKrzEB4uL4rqegNTX5jKFV8GUirqgbh+I+BNNH5jqGYO45sE4hlW9t/mWSFoFfMvTuyLgNj5lAzbqoWhvlZktZMcRN54UkySEi8MX7xmXl4St4vkNfJLiwEu2W59LKoqOmMQPWXNp3OdcSwnouUhVdJljqOBRi/cCMIeJVsVxK7q/lMEoa/iKrfcobOXmH5X3LgF4ehH5zLwbWmPGXEOjsx3Lj1GWVthtTjVYjvwu1P9IiBZhZaqteYBgzfTErdi3ECtPS7hul32vCYQGGC1LVDAfJu/z+IW6O05x/THv+bjPlckvCmCyCHA0a1X8SATgnSUKI6RAY2CokCKb4SsFagQZovSLq+r/8IJxteYwsvQaZlD5CYZuotEp4IRAUVXXzB4t6JYAOTEA5CDuwnCM9PvP+3aGqZTnF/wBTYw3iFmarpJUVYe5VHK/+SgZZYgCo4sYSz94RQ9S4cCF2Fy1WzDNYinXFPonyEv8AUHsu5jV5PzLLkzLYAqxWizofLlh9hpLz8Q3HwIPuU6EU/wCIWA1GjATF1LjulYQAcmmpTxXkYfUah60QgPuYFCUqHnGY4XmLa1UpbUCtjkgMWy+pWkvG77Y0+mAiP6igok/ODr6jM88R7Z8wyo+mIW82S+hdYqV7NNf9+JWuT+kVxy23p8RuYgRRhNuh7lfMb0uaydxxM2U16hQ37hzP5hUlllSZzxN+aCTVVO+TpUS04YNu4KkJgRcdQ2tMLBcy3UVRGWOi8nwENWVY6xQouBEp+SL3Imwym1G2WfjyuoYht25isTFXOeI7OgSypasqlBs45gVvR4A8zMSVrdO4fdvQHqUqnBmOAxuYI+OPUun+U20FiDY0cGdY6DAl5Ay217hdmZpqJfC2Z4SJVpeYqz4zmbmYnkGKt/KNXkuoaq3otHsl4K/6aiID9U/mkOmyrKHmiDUY6qVvDHpslmUFeLXqOy5t2oc5Da9xa8k5qAr9UVRd5Vzk20DK+iX8NvyYarFeeUGCLwMQ0BOCUqXlTcYoINwYHNCGwNSuGODgVvPcGLyxTr7iU6R8xtsEQ3g7j8lAtKbO4tj0S4PkwrHcyW4seSCrb0mBujr/AMDFXK+LnHn1MPVhdGEKseeJtHEYvd5mx5vwmy4FYx1AtB8O4HwdeZ8NfMYEfQb9pX4OqVM6A8RbnfiVMB7fcfZ9Yl14IUYg+4Mwe6jdaEx3EsIiZ9JV5LXt0v8AVzlWg8xjgLnQgnCDUxl/M0Oqce5kvjzAQu0Hxt6IcSmZTAp5VPpI9F0OfEEqo9s9WIr+J4Gamdy0c95fPE01KuVi5pBuFVmmMOFZEhI6tH2RhhuLxo36eYjdLuLrm8hnx1ADQPFf1KSFge3mAHB3zFg/tXiXYZzLY6pWWGn/AICpf7j+RY/s/lgqbW5LiNIjYtQds8MZMCug/wBZz/O6nAl4jQtvH+/UW+QJkmZ3JywfEsI0PcdyA6MHo7qYcEgYY41C3a042RL265Ep3mEer8EoKrjvuFZAqXGmNnmU+YlfMpt4RRazQ9sR+wlaAo/iJjxjdxA4utTK2K1zFqKuCLT94+o4SjzBRQ9swG1XXiHVbzV859yxA5S3CdmMn+v97mtoLh4n452xzS5hfLQaizvfU6CwwTMALiYsQbXiYx5i2lmyPTD6HtItu2K+0yogB+PuOPUdRyoYZzND3K+5/wBBAXidm42R7xDvK4lDnjzNbVcIWT9zmP8A3Sl2zzN6JgZrvic9ksZLIj7g02lMv8TFTneY4yTkqMs5LrPEUaK/UtMPSJYReI5qRkNpfCNsNKczRseZmnUAlZuL0uUnGWYMRe+ZpqXb1NP6/wDNeZhc4JmuJYUoxQg17gswDek7nbmIF229zNyp8z/gmR936lMYIHt6mPb6mdEro3uGL7D2xqvzChRzbERRirwcSwJw7uYfsQpWQemLAq945hKKUYzqYc7rllznTTULNVfzLszKmHQe5rBjzGl9zmZi2QLZklC34har1OMweeviJd39SzduWdeOJg9k4mw1KZVvEbiuZXnD5mZAIw0uFYUeHcFNnqNpSy9vzKLc5dfMvVwDJUQjVUN0Qr+JdBTbEVFS73UAbUDCu8dXCvmZa4eZWwZdQZW+JjFe5c4iOGviOCJhlReXEVolmVxLKEEwT3WY5FV6lYjNWi4UOYNQz1LZkHU5S/4uLPhx5iUUZaWc16jloYoVAz4Yog7fqJduQ6nOn3S3u2y9k0GbJ4lV/iWhllGcwEGeLMwS7M9zOUvxuKvI6/76/EGjybS3Alej0QWofMqi4s1j1MCYUqHzUy0gri/1NOmYSrS8TJQP5ywQV2yu07VK2K2bA4JSapIpRG6GJkGCKpeZlzQjgaOamSpUhXRCj6VBQbt5h6Zgrl07+YmcX96jpeFd8xRvXtmy3lcztQpzgfqB5THermUeOZk3Hw4jHJifM+IB4Y4mdpFgY41EYjacOZj3NJKNJwnZ7hbj4hQbhDddM0qnmGJbUa3qPLlif3F96mt78RW3EpcoZGO3iX6R2nH1F+IDUtvxErU8G9blq3+YLJ4jrUS5pvmGHOaxGln6h4v7isGDzFJTFaXD8J+EL5IKw4WzMSjq5rP/2gAMAwEAAgADAAAAEJwwHNTFOs4KV8A/I3T9DKY40x3XzzaH68c9WjEzRvWtWUmKIqdVKuLkhF2/3LvlwH75/t+xEngH2wE4JRB0y/ywbjkfX4CBxAxbMsy36pHvLn7lbIF69Bmp+BsrlX6a8yGU3Pg17Nu6Hh57SfJ/10Xr8L2WZQEurb3kA4H6/N8aNlNRHBJPv3n4mzrZkka+VBYUzIz6PemHE/fewBCfQeyIfJoGBaay8DANrDvgO4hNz7POLagru3S9t32eSRnoiERxVcc1ffBo1mSWPwCOB+CaSrrIooszw4XEHFAjPrFXKH/xHHmyQgKXiUTEEo8+YMem/i1XdBFm3z51MpoYXdcukOSQJS/Kt8gaMgmI3dqXUFvDElUpYigPb77KQM2n9BdkFSYJksiWJcy+n5p/OD6K2BhsJiojJU8I5n+nx0pSJPXREhQDT88t5yBwe+HKFmmJuT0j02GoY7NiUyZHHH45NAkRjV2lMJHyQpHGv7GlD0jszUh57EzBBTTcL1i7DFE4BcJPJQIJYArc70XJagsP/i9OekwP/liAolv6Rt6Xb1UMy6oEitVDPRioElyQLmnAAqHGLppD2LjDsJj2OZTBgzRbplquoeZx/aOj/VbBf8bOft+jz8u3O6f+vRUuhRrXcc8qbAhCbHEt/wC4GeFNnG+RgdUg+TdKE7l+sSd3ThHh8XnTIH7Bva32n0ZRaHcCjfo18Wa4k0U2gcRDkjBo1Ws6Yqi3Hkwj5m21R4SMTm8UomM9s+huSr2pT6n2Vbf4O1wF3fzFptsEFSohvLO9/v21Zpeu03FQapNbqftv9205/Lgb6Lk/eEvJZd/52nZ71LiqN60u+9uLp7+hZ4o0/bZq4Q1/9+Nu9tprQ3j9qU02GstKhV5rtL/da/Z7Q4yqihvwDVv2ZbLtbVL/xAAiEQEBAQADAQEBAQEBAQEBAAABABEQITFBUSBhcTCBobH/2gAIAQMBAT8Q9hbBjBOCejZ4Xl7HVoHshM4FICLqay9xbfI4zIOBtj8jYmdMuXrJk/wDbLsXtjj7ScbwOSA6Jzq7ew+pX+Qn8WmDxlHJfVqIt88nt8syDxdO4PrAHqeAce2dQ1kqyGOX2DY8CwXjLo3Rk8G6Q3llZjdWsSny62jbnd3+WLDGHk66l64yS0s4OoB3EJqddWHsdwjWMW3TbEG87e2Z7LDCF+2BbrtpfI0u7uHuVbt5x28ihzglhatX2bB1JYz7LvkdWpVgbILL7C+W3ikcJcOEdbp7LqA9kL1IbrhCOrbbUtupyTD1dvZSXTrh3CZPWwSP3gVjIfsM4tTv2HPIUtctyBeruFbG8dyCxtWSHDJvDq8CfI8sg3qH7ALJ0SbxmeSK3xP1JgjecLtgY3Jekh5De5TJNTov8L9eDGfezxNalNmbFvcdkW8N2LGDYth7wa4MTg1H7Yj7xz44AEYepXa1lsX7f9Tj7J+snDWd4zeYPyxs4meGM8e4DaX+nIKpZS0tG6nLSz+wQ6cEPkCQksmK4OnCFhARGfeGFll975MGQdyTS0sSJ4LqELT5dflmzYYSXhn+yH7KcjImyiB2xfLE94VtgbYsWLRsPlhbH7ZkWbPAHJP2NSZwXV7ZZtljOvZmj2XxxyHVhyZJnDpwC+2fl+kP9j9eB/aR+yVmOp64GwgLHt1dXXyz9k2cWSP5J+OF3jf2/wCcHPyHrb/icfI4gU3+W/yUTv7b98M/HDJtF23tZxcPnBn9n9o29kSD7wd/ZY9t4C1ag6vLF1dfbKdML8Y363/2AvPLu1bPl/laTy1AY/zdZfxCFv44CWk5dWEw/wBy8BBB/ChL5JsvYWdfZH1dobVq2tit2/s0mv8AzcTeDNg74Bl5OfLSZvc2STMhEdOrsjzkW3rhn4uls2a2sJmbbbz1x84y6eW9cLlu2WTw6jHTMDLp7gpd5dwAP+X/APEF9jPdhu/22HZZw3mM/wDqMdCH9LZ4t5NJR8beTzeQ3+DLGy0SfqJrh9lFXUgfX5ZZkOQ7LvIw2WJsSF+3th+WF1+c/wCIL7OekLZsfvA5w3rf4KfJGz7v8SCgPk0pj/ljpt2R+oTgG8rru9QB5CGNo8dftl9vMdy86h/t1+WR0x33als8gXpjXvEBt62ONZN9kwLCzn1O4tCy1hcMKth9kDqAO4B9geMjyVe22W1/OTfoTl1PBPpHe3YIZ02vjH0v1kNilq2xPG7P2ES77A9kktnbK9Sn7b3Jerdkiz3nIfhbvy6fLV7u1hBX+HA4WfyCx6G062fxPbseb/BDrZCdSwi/bLTCW/vAoPyxsBIJAjLODpYPS+mWmpxJkGPUliyvkdLKdflj5DSPP40W78nvTYs2YAuvlpGWP5d2TF9t2Ptgtmv2I/7PYupP8k/O9hFrml2LuVtZAObDrJheVv8ADhh+xQ21/LVjbq6+8AbgSCR8tW5Hy1atYchhkA6RCH5YDqUTHIwAnSD7w7ut9SXM7l5ycBXCBOFHTYz/AG1DSGdt/qEHft39vEJKThbsvDgT+LrMX4yRnR3H9izyUe50y64Bfcg4l1/rqRidEiz0wrf2HeBy+Xfsre33eMMIs7hmdEJgetsI7l9SY5HlqG/SN6Xkfb13P8HfGgbOrY7nthA6m8SDy7d2bKGnlm3f3bdQH2IxWwW7wkeX28G2GEtIftq+xl1X9f8AypRByZdWZ3ax2QzrUA84FYXyA8I+kovXHzgjrn2O2WdHBbeHpbNqGY4ROTu2n6iTy+Wnk9O4gEwdl4pWyKHJBsvRKbW1i8h7Jg15fqT7ArhwnTZB9WtQAzh8kgUpHcQ1syOKl39vm3b7CLYEdnUYOr5l0Ykkx0WXtn3OS98kfPY8TqPYN8kV19xt6reyQ9SvljZHox6XQMhHGkvLLAm3+L7kIsOZBmtn5YHC9sW97nyIC92JtnF2+pwDGJaL7foQLu71ukCFlaO2x2y+wuoLCGalb3vh253Of4l1pabLJm6Id7by1w7eWkYnWDqMHBWz6lLLHLFvCqz0d3RtunfXCrouu6N1V7g+XlTnjL32G0bAebp8sjHounWzb/nDM8tfJMvfeNTrJR7FM6JXfafU7AsDu343afltS12Xy36Y/CXt1BDVaf1Y3qzXC6OuNtjfdi+oT7KN5YZGQJFwtyR5YvkH7CLthnT2zIwZPmw1gbtuB6knTLu3YclX2e7Ft6yE+wB6ZuhDSB+hs+p29NqMgYZFIOvs7ZfidMLtgfl0O4TtJlPC67unkn1g35JkjAkOWkMlmnse2d7/AAnRGbIWbYdWl7n7lvIFerB2VfYc8j4EaQnU95Z3Sju6O7HGi92IdOAo7Y76cgjXuPV29hyXb1LtjbI+JdIdXT0yJ7Hs+8PViPV2it6izWDHUIXeHWT5L9bFqxu90n5XVhMN9b1pR8jqZySJMB97MsR7eQt7lXr5GiU9Qeh52HOBrqMcAXpbzBrg9E6YvIzjDjSbdywlo6wiS2PbRt2xIOvITOXTq3rq3JYze5G6Sn+tWrUfqcD6nnbemR7llpwOsvO7l+QR3aZ8Nsulu/kOt2DpP/22eNz3g4HUq+/+gz7x0F0FnAH2zacgej7Kepu3zZYL2XuFzYf8JQwcaw4JjgFOo+k+8/lMg3+dtuovCBUvSO3JMjPc9rBd+iXWSs7l1gI4ewHt/wAngu/z4/8ARllljC84b+X+oQeW/s6WgctOlpMGFHLB6u+l2mWYdyJROpdnqzhj/wAA21HXs+zv3nNk74BZXBwZlg77R33HXd/m+2i19t0y8Twu+/zv8vO23lvDbXzjA6yMmsy/+zEdMrKJkr0JD5xvI4W7/Dyf3vO8ZtkG2IHsLxsv5Hnd27DePXANYB5/f+/yPrP/AI4Rp48CHt/uzE6t5BfI/wBlbEvcOf0G3vUgTHc+5bDz5/OSlsH7ddrd7tf5TbczDOv6HO51bztv87bbb/6hvP8A/8QAJREBAQEBAQADAAICAwEBAQAAAQARITEQQVEgYTBxgZGhQMHw/9oACAECAQE/EAt/Lf2HGQ9sHIDlm+WYXc5AnkUe/GvGxTjs+S8dkXluy9nH4F+EGP0lEsWEHh8PIYxsJ37ZuHL+sZ6z5lg7C8bK5C7t72JNGjQm6YFZy8g8QTOS5LsJ/lqe3Xt20jHUfo2M6+3YFi3DZ1OEH23qzLH9kxgE2/6IBsEaT3nxA+mzJj/Yt2/UXdk0umsJ5P7PgvYHVjxQYxqtsLa8hpO+ZGvpYOQjLUFkGXYP342V78PewpyzTCK4geEZ7G7DOzc8ZOf9I22NuXTse2J+pWMLUnYPuACx3YOwj7GLyw2AnYH7BJt1cLe8j9XVuxy1MBZ+LXTA4QU5Y9W6gQbP9rZbnxhnbByb2wL6iIQMiZPw8gJ0wuA3BC+5X6k5J9vxnNgEg/UrCsCBqXCFkPe2PtufU4tUFjWNefCjRYzwLT9SvNtwCD6Reo9oCzbj2WAHbHs58tPWASZWHsqw5z44+2Fr92WHtx2WX3bsmuFusJeFhvfLtyQvxnNveShB3VjH3cPZ69jLwb8IQ2ClnrZ/cPbex6QiRnyIB8sWLMssvWSK8ZMO2Pu2e2hD+zj1hPLtIsuW1jPYFwk5wtTDlmvbfsk7KZT7AORn1Azpf8fIE3yMzSLfbkYS9hMJhokWRnRNx+yM9tLb5Ke3P1aRnG1n3gfuEvb+kHMJ8Rh+C35LGdj9L7Dan3C2MsbNj+4MD8lIXLWQ4TMO/BwdtT2W6xi34Q55D+LvtieF9gsfu8lZy3yIoWmUtWj4vw2n1P8ASF8yRnJr6Wo/UP2g/Axn7sLljI0uz1kvIVq18NmR2yv6fi/hKiAvbjybu2CXqRu+r+ywWk45E/sv9o+MXI1IlE23XkoLfwCBuPYGXXsj0u2Tnwsp9EvbhIahLxH1K2S8bUgZceyx7a/Z1sf26ey25h6ZAIDH6WkEiBknqFOz9pOS4QTI4GNu/DTUfa48v9mUfUfpHYBf2hPpj/q31i9DkoYJa/cBws+1w3lgd5C3wv1JH6tPSC+Ww8hZ5CPqaAYwGQlpnLRYNgWM2/tHeXtZ55l2SEIuYFoeBfRI16WvMgfb/wBv7rV9j6mD+2XVP9r1G/uTXvwILp4RmFcsiWT8sEHdfhZySN120Z7ZyN8ixFhBnYE46WD/AHP7Jrg5O3lh+rB6R9UfXAeWOLLcthjb/SwuZI9Qv1Kr2DHbTJB4QOm2jylU2+zIY1LNh+BMSeRsK7dg7kmA7Ze2wbBfu47OsYB3J/S79Z1n1tHsHOXL7YHSLyyx/eTF4TgsZLHY155OvI+kO8sInt5K3JZy/Lucj9wPYU+CS6sHv7iMe/8ANh3/ALD/APkcn9EG+QxPWSA8gHyTORTjsbm8myUv4249tfkfqQPnx/3g+EkGTOLz4N+pS9+H3sr7GsCU23dJ3q+hl15DvX1YgdhJQ/RdeS9lG458b9IETQuMJAWQbyVDCFcb7TCvWQ9bv78b9yXHcn7kKAPl+XHl9MjrkqACMeIclheSTTk+PsfUNh9W87fA/SU3kp9tEsX0JZaqyoLvCWH6ufDbxIn2FzYJkfhxnl18Eekg8Ifu2HYat/qX1KPqfwsXZeEY19+HvsnvD8HPFz5Y+WfvwjLkeBdfclcYh4klrAMLPjkhj0v7YR6yRtWRcFsZJ3Ht64JD+MOcdkmwdsj+/wCIijyw+Mm4XlS5/cQwwjXXrBMDLv2CT7JPYaxekNhePbXBdut4lgZD2fPYXrsLnbVnPnwEXF6upPtuznbz+X42IMfRBeSHw+MnGScs+lw24Slt3ZC57KOEeTKQj6gM02+xy0zU6NTKPkDHLSWiokI+oXsFwMgq8Iy7Fzuy2EMA/hkH5ANJhyews8j6CZU7tj9lQUzLv7Z6bD6lPhBa+iRaLLj55fmkWu1kB/uQ+D5/tkrrH2ScQUi8gAQ2dChaXGAiP4ZAsKDP6ICCT1hZMWluXs20hvtlO2DkB9RvsEsyK8q3DToBmz11I5yFUT/i+hK7s+ftOnbLMBInmwBwunu/xG/DDztzNvujTd5GD2dfV+EoYnJBH9ScjYFkQgtIXhHqy1f7tZycPZFdeRHRsC79ckGBGXJuEvkBx2R7kAN+og4fxySuzuMOMAXnkED6gh7BsALSI8LvhfXltZsroT4T5R5BDOF42BaW7RrAjNfyLt5cyOThp/kmIjk9ky8JFg+HrtmX8gLu4LhyT6nPlt0ld5GB2d8XvtnMIYy9jxLhQgQB/UQgMJMI6bLr+QMf2EnHln2EeWXh8cZlpySN/wByswdZZgckNdoLSXIvwBe/Gd2SUEsO2GF+5R/d4jcNnL0aMuGs5ewE34XDWE//AMbdxbHXluw9h1pCJfpAGb7cDm23XsJ9s3fqBvdkg5DZY4y+yxgyZwNsNwMbCdgDIWYmjxODhMOlo9l7eG6/2FD7t4Tzfd2wU8sNJagHLMDsvuMqI+vpek4WhA8J6cttf7vX2xKUJ+zVj02Dtk5a+t267E8PbJsMOMoE1P1YhdnsZI4WQFg8M9TJelpwWL1YsUhgRpBFjOAn6Qk/svVZGvCY6dlgDd9WTRhYdMfcwvcF4lyMOGxbsbNhNR51t2XCLH1dUzHiQcikP2yR9o6maolicceT8OwqxCLf06MSYb2MQLyTWwg5eyDhkAzG6fdzMgn9w4oqYshWyZWnpsr3ZMM8kk5xedh1Kog76gJwtJX/AMrC5dRNnHj/ANhHMhMLl/fv2TjQZ0Hs1I+/efURNC5pk/I2HdyIHZ+xkNjf3YGpG5OTVl97OFJ0xj+Q6YfAAMYbtg4yHDLa8iwLlX7kQ/V5Eiz6wMHjN0+4yg6ynFtWH4ED6ySQdnr+oLhyzpNyz4xYELkoLm2CJyLBtlyQ4+JsyIbDXIP1GDMlOLPzO59yjzyBPeWhxf2CAY+7Jngk/wAP/nYh0n0sEDYHk2jkYdbHdJL9XI+BVr6Ieg2p0kM0h37ihX6ISF0GGNTIy8lr/VveWnLbASuC2dyVcjRwhHTI7t3/AEmE+mQnkcdyfL6z4z4B7OwiNfD5eMsSfnwuWGwSeLjbMd6Q+nsea2U4Xsy4R1whF1IRZB5F7WUf1E+Tsy+inAMkTOWiGfD8Pl5aWB9kB1dlfGQ6cs+Nnhs4nbOwHZNwkKGp7S4bsT17H2LghG0jDIget2U4THB4WJYhsE8hK33g2pm/v+LJ+WB2eoBbb8ptlx2Bk+gmHFJEoP8Aq04Zsi22Tlo1PeEO29du3Fx3s+eQYei2n1AtYXSGYeRD/wBQM0Y0O/L2/VlxsWNln8ss+MN+IJjO/cZY4WbZzakM3p3BkmsjlHi9lTJf+LzB/uWOcZriTr/yGfy8gN5/lLXP8sR/0sX0J/WD7Ky0bPoIWr0bUwkWPng2DhfVYg9xQR2IAfB/FT7nsOb/ABJn+QYGqZfoJ/AQBy9jcmtkfZHkZBKHt2+Wn6ggw/m/4dt+N/hyyzLLft+RGVof8IZmN3vwg9bLhKEa5JsIY/8AgP5Ntvw/iv27L3hll/Vl9fDOQB/9GzFnwSE9sMssztm/wz4z+OP+UPl+c+T4Ph8vbctWz+G22/Gvzv8AiHP8T/g9s+G87GvX59/y7+Xv8x02Z/fznzkEmfzBc+CZ/ANg35M5kGfwD8rhvz//xAAlEAEAAgICAQQCAwEAAAAAAAABESEAMUFRYXGBkfChwbHR4fH/2gAIAQEAAT8QdmNiyEIJ9sCQ5gRFSpdzPxiEWck67nzgIcbWt+3pkzpQhuPXAJSAdjLMiXW1Pb94Pv53X2sUGiWaPOQC3JQqDLOSvIb3iWRKCMIjQlSPf8ZDSLLbX8RhsRyognx6fjD8AWIeXfGI4N20/v5wSjhFCscWRxB/OTGCFDbqMComWuOf8xhIV6Lj0wtQFHbgI2HpPRgVW9LTPtvKwjQKQy0K4kPvGJoMKjC+a85PrA0sbhXZiowcYR6tYGSnE/8AGO7pZht9PPvkzJDvtxEviTkIBExbWJFLusHO14xgp8X+sihQ9CH93klWBA3QX/WAcijwD9r4zWgvZTl6FQVr51NZMzOVuOnLlkiQSOpwIIBALCK5ySLJvAuyDBWovkyGK+WVXEXNqeXf8xjEzIoejn7zgwkFcQ894YTvRnvn0wFpsQl8uWpDUCZWOjDhq7UfP6yJpBJC1q8SbJvwZrCnhM7jOYAKQiPbx94xIEqDELe/3jZMDYt3f74ykwk1feaydSDIY+WOMXpiaBHo++QEoLor5t9nHcBoaeB6n2cRzFKjPXMYwyBSKeh6y0YtHx99MtYToWuOs3iACCxyluJAPYe5GSUiFzzk2EEL8uCmFTzWGvgnn7vJpgm1Ilb6yqJCgCdEYvSyGg9QPf0xQ4C8gpj0chRGVG/0GElpiOHrl2Rd6PE/GRlqUYHwZb1JXj58mOAnEjE1xHvhp27gT17xaohydnomSRFBqF8VhhChhFnvy4qQWUNnG8CezbKj4HDwFgq1vg9HJQhQzod3FYecGJOFYSNLPTNIuiLZnjvIERhMUuI6n+8dRsSAlb88ZO4L2BrGpqhgKf1kIJo8x3LkLIHaPnFGVUwo/wDcIABG9s+2ExYNsa+xi52BVrGjHRSjgIcHlxrk/wCYqSBpxm4BFTs/5gSCxaEJ7YxBZCkaxLEqKOfm7/zDFGhpGfs4Q4kSYkeYwkAGzs5med/7wdWqRBb1kSWSnZig5IMVJ5vFskq0Ctb9d4OhJ1K8D73GTOAVAnsUqDFxWAKRx0YuFYQjx6a1zjBTBCSb2vHpj2AepNePtYBoWFU13/mRNB2XzHbvnGIySIFIPF++CRE+rJbjEArIwoVOpwE7FJ/ljuUcMOXfxhBOCUOldnnHZKFZgCLyAuUg+zjBtqmy/wCsAzRKNh/WcxVqC/OMNTSIowdFy3pg84iE1Z4XCJKoE/bWFAB0hvJ+5RkV+cji2mJuchsWEQxikFinr7WEAUrgJLz1kTWVUZNZM2K3Tlq+L+TIOORIlTeu/XAB2E4Gqi196xqSQsTc+mQOIwbj95IlUQIlie/jIv4JWBOff4Mi01+A4/7i9TEILG8pAODIoQ1ZMdOSi0SUGUROilsr2xxZNyBx9/nJdJWIQkH5ijAL/t3rS84YG2IdH1wsXEra/s4noAmy3tvLwp0g/rB4DnIy+MZImI8GIySgib9esTwsWgT584MA4KPwGMmhBob/AMw9GVtI/GKiUigEfXDoiTxFdRjYk9I40VWwVrY9T1kUgaVvUyYyJmZwFQS+vv8AuOfgFOl9vOS+l1qsvDese2CidtGbqNihF7yaw4ip2am/DgRRCDw6HDmMMtSb3r3wCKkXSSbrGDjDSjfpORwI5Qbl85FIEutPjINgew8OpwAUQSpqOvjCOg+njnveXQTRM244pGEiMeNTPCQKFoBOIFLhqZ1+cdGMnof5kOhJ0zPG8VRn8vQ4EqjEy37YqzgPfIuYDwz4vnJz1WMnt/eWpDggiwxcJhYlunYvc5PCCqQB7ZsUgibd+cCJG7Z+MRC7khJ1rNWECRxjajxZzD6Rj7Jd9vt4ZRQCR9TrFpL5OckqMtwNZECOndDkA9plCXdCY98EDMI7dcYIgEKCL+/ecVF1QFkF4Ov9xKUYiYrmMdnESrGCMAUKQma85ZATTNFcYJqtBKMEAwo1N4yyklvwY6YCLZf3kLKlcPvplwxbPeF5AMLofOE2Hck/WVb2MMccRknGZoof3hqUhcNY4pIiUPTIZI1sKcRil5iT+MVWXaljIQvtXOOJCHPphsHkH7yCkI8Tigc+09ceCmu8MnAnn0yTCEcZEZD8RnD01DFX/uKBQbqHTh5JZ4FEzNYMaXXeDpjFEk5OrvefxhEwQJDjG6JHrcTWKRASOj7PGIigtKndD/eChAUK1X5xgKpsJV+MXVWltnX+5uAhcvQt+mVLyWTPpkhhyRGJyBkDTAbyzsQgl1pw8RI8vPthgresEy19OMnFkKQYGM2FCPnJQiMSMYQlGmX7wKpF0o4AanQawjAAQE1ku2FFXhUlRBepqsk4XBbX/uIiZEhht3WE9owIX23rDE3yMj3xkIwo0ix1lk8NQn2w5FF26xKR6Mf1gFQPWSEUs+XAit5AvGbQOzJSSdIH85KTOU7ZMdCNRc9YJCue4Jh0+35xuJCQP2P9wCAitp9mMma59PWJ1kFta8e+AQjuEfrvAGJkkBxh9kkiaHIEeVmAcUDoNrAQs0RvDFIFifv2MrnlQbx5gvnDEImalVemRQCXbw44swl5f4wNJnccvWPpMXmGjIqenesOSPSP+YUMEW4M5YGOTWbRQcGpxCCyWRZwRhSXP84MFOETftlUCOHzkuIDzo/WTsikbqB/WNgQAtgZaxtMYcGzgZCsSd5DNGmXTlymDcKGFBwfB9ckAgaBJmP+4yNjWu+cs4F2HPv6fxhJCCGdsk4S0l/wwaUPkxsCYdY44OUowSTDxGIQqYnO2IGpgnBKnNsXlVbOvpiaMFEwp3GScBUzQVh1SCVXxhcDBcb5yhI2aTvxivcqdRhLOxDK/jLCSY5OMYKECVggpdGMIcCMxIZGJRDZFmOCnd5pJa+/XBLAN1k4dBdH95A2ZIgDFtsLqI9sniGN/fXHjYReg/zAUsRAw68+dYCAoNhjZxeihhOVtsl/eMykCDUt4qcrQsw0iDGxj59/zkE6JQ8e/OsUkQkWBJ3d5a80+TEqu9OQ4hBTEOJKajU5zDbNjGBgCHuPnJATYGM0CL/uOhzWq9cJgSmSyMUEl4d3h0CtWLUde2XieYk+bxKaRQ8uMsLDUw4ILKahxHkFKv5yfW2B9amAR4yeI+hMea/eC1GZ9ycnEALczf8AOSLPTnBphpmgYsEAJ7qf9yQ2A6/7gUyJ1Lf84Bpm7l96nIQ1eBr+IyNQTpOnj+8NOj0B7ZSgHP30yIyicQSK9Dm8PZkQv7xiYEqQFMYpR/GAiodJ/eMECYq/+Ycqm0RvFqAjofHGERCkoTGaGQzHeMhJW3JAlee2CIgQ1Q/1k+cO1YrCzDdGO9BliGsptfHftkNgqFVPf6x3paiJLy5SzMBXG0j6u811kYnWFIBhh5E06hzQFtRkFsO2DWbj3KxgioliIwAwnofTBxozElMmNvm2PzjIAU6uBwmQhura3iJFlKGhOOztSAN/rWa/RsgxSXEkVUIx7JZrIG0BGoxmBJPFc5AC8Ita/wByxkRaCR/nGxCQhqKxdHntxDILZnowqUV05MY4OAhYgJg+PXJklUJSXWJLOMkcRLtNC6/GbQ9+Bg2GwrYfwZEwAJ6jzgXNxIre+ceCmXX9skdM2AxghGbhMhNkb2+MiQyLZVxgKwioR98jUliKFwIwnor/ALgCCjEXmkrt1lAjUAxiWYOwMINJqRr2wU4ElwmJ4c1jLAZ1JQx1pU6RP5yAgq3GuPvtkSM47a9cBSFrezGAVnm8CNPQOTwIe++Jy6eBjAMLTSaxZRL7emSRqRY4xUIPbFhEiJLgUoR31M/9wHGAb4l+3icabFC+r/coS4IrOuIOzNZESVPnkc6BHnfWNBLBSTlOVOpEx6JhlgXMR69MI1MzyH9YS+k+zFps+kPxgknMCeMYJS2zWBiyaZuZyPks8hiqpHjN5IRMxvFJJ7VjyGTJgHRf/cMQnI894CQKbj8ZMRnsgf3giR528Uqa6Y/z11kgTXrb9MHb+AP9YKAG0TrEH5Sf8wKVWOMgUbuHjGDinN9rZWKpkPTeBZHHONC/U3khoLhgnOHpPlyHYq3NcTGTRbkft+PjJrExdDd4o+UohmKhP05L1kO98mznv2wbqQxsxgRDMNz6YugJae8JMrZ7MgFsTqsM9tOJ40BRt+Mi7QYDvAwFyNpOIGgSpg+35xTCJWMTj5VP3jLigsDYQZHaQHWHIhOpYwC4TgXSXyKPnKXQ0erIZYhETeJ4eJBvNyUdYGYKpesOFHSE6wCMDJtwSAtiLnzgC9StgaRzGmInJfcWzP2P1lXJsBP+6wlJGjTN44gs7W5xQQyStJ5xrSRleBGNqA7LjJ5QNscXM+uXXpMwdCavznBATkxzPpORKYBPOIZu8zXHdbzRntr9neMmHWL+MtDBZ65eBWbuj84CoHBlwwoaiPOJlIX1ZqurTiKEejL74zBs0OQUKXcP5wAqalzjO1eReQEwgqRkwTYdKpyAshue8JaBOV/WBCgWt4opebBmoQ8lG/ziCoIogyCEBObxqwXW+Mj2Asr4m86wFhV7AxmlDpqcj6E7KesZE8UaOmj+DAUKSYisNSEaxkWOzv0wyC0rGSTKD95FkDywSkgYgOesBptTBrnHVMXAuHBYnSnXc/GRvFmW1tRjjibS09R/UYb0MHCBJONZUP5xvPTkqOZeNI+LvBjWOYUgW5RxPGAYERQzLNkhN7C8E7Dwl+mJU7C8CkHcF4ZpvxOCUGG5TnHICRcrT984T0iQhr35xRSEDutmpIwLomhCIwkGSts8mQmc9sRAwX6GMahS4B/OIKA7JGEcA4YZj8YQJDNsheJHCqoA7hfsYLJOYs7i+eMgQ2uu7yRkWRFmKyINZ96ygkiVGcYnXjEZZQZykQkqcXxxBZZ9+S1/5kEAyyDQ5xiFYhBLzJjwEQ4yFsWmIl+/xjHNbdMYWgkjFH2MZwRTp2GIhHm6kCWSCmijmQrASzHwyC3GLAzG2g4+Y4GBxCN0nsP6ycQBN6cjBLWS07nNANk1URGWwFwzddZagyjST5ylP8E+MCYCABqOMH5hSC2bclhnYP8AWQClEr+2jEgCKhkxjk/k4AIeDUv0wJJKsxCv3m9D0jFDAdDzgL29SP3nYwYh2sH2sXDWaoM886ciCCrFfk/GSiRidsOY/vARQkRqRv8AnFMsIVk8kD2TkkixWIgb9kyxKuGsZsmG1jWMGYsPSOEEICcoVBITzhqPil64IDdAx5v56xMlCCDsr/MiUTETOxP7DhoBbNr645R0RCLQN1ByhtyKxo5pYKb9JycEHFQJqTCZEqzBaAZlkjmYdxJy7wcYQKVZc5Q3tiQDHzODcjso/WKEhg5FjBtgCUJ8ZfGbcIGlais6/lo/0fvI+JLVz3kEYZVll4ShSujvIT1UCqOAt7YNEgIVkXrUceOMFKyUZEjVk94wyxuhE9gMfGjdgg9eucSKqgqCbqfu8WIvFVwP/MEQDazsrj5xjwwkDkmll/vBhSbCXsXJGGloqBKSuAvZlnWAjgV8ZBuFIJ9Jt/rDvLooC68DXOGxRNgfJgAy6PH3+sRLElcv6xWgHNs+PwZODBQVhZIyuxPUnrlm55SsSl3D6e+Eq3Criv7xmTIeevOAsAySiIvCUSJFqIURRE7eIQpE0Q23GOyBRoDoYAYjLEYgylEBEmcoHEaf3iosXxHzjQJuiKwTlLkVQGPIaSwe5cDgSOEHlRHJmhMI4kUx56ySvCYY60M/JkkGhLJ7zT2DFsEElpm2hqPXIduVpNvgw2liyW8CxEEyo55ccCs4TkKAhAV378YaYXFAfEeclx6CCx5sjFjaSGV43LzmRNczm43OCyCp0Hvb6fODxjk6P4jBYDySSZm8jDiwjfz+cl22wyrHG6BkVa155wkPAGCPVv4yFBgmU/Gue8I0/IXcbON+cQeHwfhw0JRYXJeMP0F1iexB7YKBwOe9VhESReMh2E7xBZCpKvf6xjwwHaIIIiL7jSN2WJkMqDt4zWABDMxvkcxAe0zgyWRKPHlfrBRrUC8SofjGunKpASIRRbWByS7Apb57cbzjel9jjxkGI2iBD2/eVAlGxDtnWXsbSR8uCq3oUUyW+uJ4PZWPaDjRiq1VQHuMYA/Yh7/1iiYV4EUyRjmsf8wjIgmoIcIBFCnjGQVCE3E5DITB5oyEVh5DERF41AOyA9XHFZCNRdeyY+ciKBWh3Ow8DjRoFpmG9p/OLmj0IjrIJ4WUT7iZCoYLJ6b84uT3jRW94wWHiyT7eSIEiIUei/rJD9iIgRj2mPbChKCSeZf1GLAoqVuslBA4ZMokbUo3B+MJUlLj20/KQhLyyY+khsTcIIDsfXIwosdNwxWiTKR6ttH5xyxt2j743gyYFn9aODEBVgEHwTktMuZWiNV74VmqdoKHcOXb53k86DAV4I0R/LXtkPPosqO5fTGL12bPGKJJZkfN+mUjSCaF98HIKDxQ89awQPrCGTmEnX3rHij2mEAAir7d40lkMeT2RD8mDLO06TIrouZ1Lh75Vsl4r4fjD5CRY7x0MlkDg3kKTg0wpPmQN8YuH5PD5xEkJShRGBwo3AWOPGXBBJK3Cc40ZKqnn78ZKSCKIaPeoyZNqZ3bloIkHeq+/TKETPZoMHiEAt0SecOnJ8MSyMEw2jxTjUEgNoUEiJY6ztYkcA+hN6q9GLlW2CI+2YLBVUrFeesgEBLBk9fOBaBJhAPacek9qCHBcySV46xcMxAbv5yYQW4D+nBkk8pB8HtlpM1T/reFFQS0CmaT9sF+Dv3wk4paRilqS+d/vJmZsuSoFA7aef8AuDUMkgeR5xMIiSVHe9+MYgNK5fkg14wJYLwwjD6YYlXAylUPU374cCCYKq7x2OoIwpskFib1jRu4a9B8YrQ2Qbw6lMRBI7jjPFZcHoYbhYITJqTIKzSbHly3T35GL0Wz6YVjoa179d+5iyLFljvlxB2CHuX96wMbEaOlK71+BxvHqILBDnWdzTkzrktQgIIfmJnBNOOMWgqKsRyL1kklUNCQ4MsfQsyEwssssnEjReE3lJsdANu+O5xNbezSPGDqKiXwVmTnm9ZvgrYFr94Vxy7Q+1kBoq4RZn1yB7N2SZI174kIFIl3OsIQ9VTOSQVklYreQ55N/wCZxIGASCGtRPvGMxRQAtvXczeHLuGARJZSoBJr5wHjPdyRGOpTec8MEC6ga8d4VIszJyMHUk7w1qcTFll8ePGPkCikD1CMXpnlbl91gjyEEFU3EbnnEwBcsr+jGBQkRFpi+cTUKb4tp68GT6ShfA4DQY47opU9E4YWMIwj9P7xbSw3fAXeTUR7LwGIhR6RInrf4yRmRs9NGvjIdL86DpA5JlHcYJxCSKEO1WSdHLoTpSWBIAaAAPjCGL4FbhLht2dvVGU0J09YVoIT8OhbXpzxh8zcpgQMKuDvAJhDmogEJ25pFxYhwSyhC2oEU8JlkIVA9DCQN8qEaAzkLOmDQZKSawKPbJte0rj3vERYGzBHvgl0ZAD+J3g0pXMJT2yDNBmDb/eH0goEeITEQaw4yNHUVWR+QiMM2q8fxjxZEqWZJ8EfBjiaYytdL+ZvC8BSiAduGTREFJa9hM3h0hYXyk9j8VxlsCJWKWXG64suMgohgAXHGCLrVnTX4w8gUmQlO39GAlCFWE95rEoaR37/ABjAVCxbWOsn66yHRqchJsGHZD4F0v4zU2QEvn/mKKFz/GGuIMTle35yCsmCf1+soIkiUffOQHS0FFCGyBwHeOABjfWKwUtEAkcCy9Q5Wr8KIszt2ue8AuWQtB03cdu+qnuojnCQKW/HN6yvnUEDTKttwkxGKtw9AsUH7rCq7SoI23/GT7QbJKCIPaXF+IEEICEwSSrkjvJqCBxqdoBviffa7UiwwWSbE8ujjbkXzoHUeYOdf91iUGwBGh9XjBZgDYGlTZ5icC9mksLy4nJbkVbTMQ7Yy0jCQmRB0m/xiEoeUxcpXjziHZMIAeD+DjRHFamyk7iOnWI0pM0Ssub3hgI8kcKGayaIyRbDA7IlZHZzglNHCBJh9Ne2DyibAKR1sRh6d48QQ2MBzTzME1rIzbUCK9QAe8uMO+IpBIt3yvMd45FtDLkazJFFL9jB0AswZtVsIgfL3gou0zvWBxCa0GIjJIAfYknxOOU8OWIOr6175RN1Pvk61yqndogAL2MVVpEmXY8tyyYppjbJ1IJqYTXOAaBDqXTUTUW5D9YqUu1Xl6xYlCta+nWCCOBRzyPL+8GqTJQB4/jD09mNzJYb87x1+ZgRBVe2EcBDcQqfmkNE5JN5lkGAVt4OE1GTRVKCFInWG1Brp4Bi3QCOOjFS11ur38YiaRWBWDOFmkSi+Pc8TxhrlbNkZkgXgJjeB6IFXSSQK+s5KlYwLpeSIHExltQISFn3PbhjNRhSDz+8dELaEpu8ArQfnX84SmydJaj4T5xR4Synlb94F0M7EquPnJxgETDFx7zvJ9klITdyvFa8ecEDxSq0cYZvptoDa8BbkYg3Zcvj9cYYihOPacAlGh6g742/GRhFS+Vf9DECOG7+cpZQskT5/wAxNeJWicfw/GSQkTLe1RbesnDClgH6T9jFmBkUc8n146xw2WCRDVZKpFDk11i2J6RROvvnCGMhLFwTHcX8Y00KBJR/Gi8dmFXQeJjxhSeiBlRxgapdtScovvIboVpQll4MnTgTbHwcUayaJMENMOqKpO8cOhmvxinNQyiX8XhAhGVptSV7aynzjoK2XoybRl3WiXorgmJbck6nzatf3ggCSIF9zHznADhr1wU7JoVy/lxVipOFkCkdRfDmyJH3384Cx0HROI4tLKEan4zhIgQ4mP5wxBRaBUzxjpuMBNsg1AA+51ieg0TlRK4+tgqVJABy3gYcehhEZtWYAOg7pbx64gAjJE/k9zDzImsekWswAHLh0gwT6ehaCV3MNYSQJgkCpnr+8oIgczpcaOY8Yi3QkBDMLI5Zwe6EWPZzJ3hBiEEF/nD9Wm4s+nO/t4/gOZSSCGN+njJBSJ2Mb7wiCsIUDNxu3A06VEhK364PgEq08cz3GXdBdB+caZiYL4in5x6EjlLyYLBeVXRxKyFyVvIXPO8RKTbAwMUdS/nHckk07GAVmxXl194cXBgk3EdP3zgJDWlLj7OEiQ5IuA4WImYeMi1OWaVT4o/GF8mDgE24tSLlXO34MAqbVKw0R2x+Me2iQjLm+sCORmgFGPT84vAHNKNod9mKIkATMk5/nBIgcB5nXz/GcVLsKh2QzZuq1OJcwELOBUw8OYJxECwtT7r55ONZKbLAMCNUZUmqwAEujlK51VZEDGoAAYKkIyEuEBoD09rcJwYgMvrm6oREx8Lf1OJhRkqdecB4ouT6dGMG2ePqfnCiw6bVM5vC9wgeJyPwGYwDyvOOKby0fz/OFIkE7MM5Ez1AsGP5TtYnDCSYAJwClg9OEwiaQNX+MlkuqvVIb1Xr1k0wAgiYUCYiAvyw1pyQewN66+TJIEeixXvvAdwFlfXpiURCqy56e8rV2nE6Hm8iuiKB7Xxu/OCQ0lKS9Pbm8nDXegSQf3jOay0Eo7l397xQ2yFOamSrE0Tg+ukk7sBDGo4wJERoUsjY9TXicaQYBCizrRByc7AQrUUd3h1ZAAho8rWOhyPLgWsQBMAdARDiJS7a27nztV5xmKISGBb2QJsw6MM9NLFjJ3V9tplhnEvAKkbGHFNdIaw3FFnn2wDJFhZGPZVQhXz8YHCewScdxbt/vrF5pJBK+D78YsdIuRHp384vrpGyvPtk8Qe6dTxiGDQUj0yDLEu9brHxxltf9ybdvPGlfesKTQJECK/zDYITAoJ+TIJ5zsHJNvO8nTxUgACK1NS0PcWqdZNPkPLG8VviYidkg7a3eK3MUyROojnWrxN0FEY6L/r+MSbTItHvxjsbgLUI6438Y9+E69pOnHt1OERsyioBgX5+cZU0sSV8emRK45xtz6kd5uVUoHoyxawyQeSytyvHOBtjZviFCZGakib2TF06VQI+ryZEvFrMdkXAx0GPQyUrZxPpYkCTwuAeIsloXg4clpoqb6nIAptTDZr8fhwFSahiX5rOKGYwggoGaOTSKIH0wALIFEYbFJkmZxVuBLn7xj3ZSQCsqUg85I3XB2xEhZDTviccwm1z8/H5xyuFBQPtYokKhWsS7QCSYZ6fb/MjTsoBPOLwSWUoHS4CFBDC/GJqOHuz4yi8bDJj+YCqTHGHi3SuqOfXG5SmJpuWuT8YpAQdElevHnDDvdox1+8dNj5b+JydTBVIbZnnFg2ANrDWADGD4x6YqCAwnblLoZB4vkx0QOSqalEtniKPXKYnmirtVR6igxJOVyyNiMAtImAxLBjOzCChNEEOopqI7OdMqM5WrSehFssVlJ9dFl6RVdS7MoNIJm7CQ/OYduxwANENgi0hiMclijK9H+Qxtc0Sk7j+zBcyiCLmYOPF48oDJT1SvQoxlTKUr2sXwk4HzmbNuEuQY4Sd4ktNgrA21yFWizSkCNSCI1kyVLlEr2wSVEJkvN/f4xQiXJPPXthnUwCQy69e834GJlMN/O8DITlFEVAc+vpvOAoEESjHjWd4MbMevGQ5gO03zG/5xwyUUJBPM4mYKQggWbcLWcgw8SyEMj9XlyRkHJ/zC+SwYkzEZIx5VCy4sx7Eqk8Rxk7kFZ1re8HqhHjHGxSMnBbHnIotHg1BaVy9BcYjspEiRl/DRxGMPVQoI8E49P1kGzkSgdGzG2saLbKpiNOpfXI1Tdt9Fczyb3vIUr2stArrx36ZGGUCUviCZeuPOImRO8nbB3/HOSoEQZJcBKwmanLEAMtRUW+n/mNRJKfBOR6qER+n3yQIugkgqLTy/DimjCZNSXP86wp/EWjnXouHLgqh2IzIkTV/GOzIhptmlVQFTbPcYHNIxLujo/vHdowk72N842uAIhwM6PbJcA0WBJ36b/zFGgdkrogOvt4tgYA29QMYwNdmvrhxbiELcoQnGifXDiiIDrJ0sQSYOd5XBEUTh11CpYesezUbUDEsccfGES1RdcXgIJAaL4U5zYCEnQ684y5hInv+t4R588pyaWUkW3xglLeZAEniJI3CQzjqdoO3deOslRAViFt9q1kjYFCSYurr6+uI5jEzfr9/5liRcweMJTNY+hVl/wC4GbYGwFeAl8+MlRJVmR+/xhe4srUzxHi3D6IR1EAfm09jCUgAkNxder/GOWi0dTMTprOJl2RMJpqLepxXTiOSEamEtxrDCgxNwO9j2b3jmI1I3CG/SfjJNoiyTsyaFbUTNEzL4aEE81XGPFlzwAa/J5yTtqKBO2Pet+mMkCbrA5u37fOGuJ2aLpVNnvjgFVJgEPreKVAp4WLMRMeOMsGwTEv1iQwuaWY9dmBIKU83y5AthpUOcmirNAxB1kFEHMiiO/xhxwRCgJN/73lk1yDV9/vEgjZA6vn4x8JIBl9W6id+cdfQjASxvElUCxETSbvsxLEIiUXDCwX2GFUgAJYITTwaS9zjTzaKQUK8nuxdgbBwoJtERE/3kTSNyh+PnIytLHZBL8uXUZgC2QAfnX1ROptTMkwmm/x5xJCdqTXt49cGRlIqSx+KqO8FYqA1Ewzg1MIM5AgmnfOCVxDcEeWOgAhAEg5px/WK2LgK7rXtcR6Yw8XKTIEZ99ZSgcWkPq+mJJxFQRKJujXiOsBBRV+IrCQOjYpwL98RDcV84FHzgrjoAQTwxkmIL34Y7xnwcVVk0qEQUVEcHnGmDYoR28+2aHJ3A6dZTrS0DL1484egDqWJgV2Nh49YymPpWI/eO29KiTUQ4zAk2VhQtAVBNsdHP2bN4SJUlNG8aKeAqAPUg9sMEVA0OjmzvC2ndELlh6+85BMqR0aOVE/7kPWFTYRYh/BiKsQs/wCsS4IVeT3984JoEjBz353k6FhFaja+rrIOhQlQsD/HwwTJSYNkKX8e/vkbANoa2nXfphhKKdYEHpDvxE5BdqUfcX81eCSELIqI3p3+MioRSQizX5vGQIEWEeHWGBV6WC59CzEIQpCN4koAruWce8YNCIAwhwnNRvhwx+UpJUL8H8Xzl4J1DRswtmuJwHBQqgg4j1wBjR1XxiwSRJq/pkMpJKZ9Df8A3CGTTKKt6ODOZ0AYOwsexvUYxZbFErrCSt5Z9MEaQ0DZyDmceHn1vCbARdQoj39WuMjqMGEKQFNhs8+2Va9BIqvYwBqJEDSD7vF402KaSJ0dIHr4jJlms00CX+fziUZikd7K3XeUPxqJWxcVFeckQAompOZ3v95EySHSS0KMjcaQtmivDBLXA/vFMANpLcDGCaiNy+cjBamTYpyYYYkJtXj/AH+cDtZgIIgzrlvAw8jYCPijp8z5zZvuz1iN0ev8iamYGJVEB6ZxDAXahPUDrnCrgog5jeQCLVBUnCZRlEEt21DfrOGrlGypn5e4wVpYCTPEOvtYuU0AeIaw6Zcd5kExfM7g6wRYsRh4o0rIYLKMPSXeDh2hC6lZ9BfXJGjEbRQQHh7KcH3dKC+usASiuX6+uMmRJmyardSZwoNEeznvEsBsUN+m+PnGhbZJ9eHDZqp34gjVRvziSWEiqNBu5n3xnxDXnHG4n94BOcMWmlejrA7Rm34qcMREQQRGqxYzCgMk/wAxnKCUPnAqgsLSv8x2gV0BhT3X7tsGaLkCebs+coQBKxGiFrXeRYxTtvZXxhobCvpbfx/zJkCEqiVpiD/uHpLksWdNe/xkRuDhpv8A34yeQTQp5NNzCRxvIfA1ksBs97+zKGaiGUDiJ8T+cXYyNiFi6eNmIiRAA1H1xJaEGHzgmnc6S+8kA0Bv098XMmhFIrBhDZN60YGRCoeMeSgfQxcVgzA67fzgoPImb/vIRUF0emFCJEKUgiIYXIxZIFYlNgO0y6kkOLqYvU0L3hDWKiG7dXQbnF4pQRmSgNu8GTMrRCNazkmHkYXXxVTQcTx/uSc4dgSRQVNZFwoxSue3BZqPAKH7rE20R4GBl9IPyzk+MRM1zHMaCnp/TFHKl6IWJsYdPhzbYaQbmr0YUWQK6Kt6QWFnOGKJVQhEe/bCkJdEPvj5z1MCbmf5/UZfWBNBKJx65CARC0H++v4zjLZk9PvthtTDSImeJ1BZ/nDJ8SuOkeeuI6vJnahu96vUb81kwUJWBM1H0wJ1Qi+C6wtKABDbRfp/vjAgCBTc9ffnBY2+qyOvn+MWpMbk9P8AuLBd0RghCIarJ0b885MOit69M2HUwkxf+ZFBhEpk+z8ZYKVI01PzGHmQZuZg2wnwlyYgtmBjiLr0Z9sNhOQXlm43Upi9ZB3aay7oX/PORhvJhDMkdEPomSiCAWAqN4l5EimeBIo1hAgIx2W3q5ch5o/INhHxjWAg7lKDtH4MkZ4KlCUDXguwGmX7zmRK2F7cJQQKiREPP5zt8pBQD0K995KoXFZJViY30axQqPA1JHhfxmy+RIW2fxGu/XHmgWFwxv0w8yoEOOJ/fxmjg6GYh9cBMmRJ01H2s0kULez/AMmMKzJD6N1F8/3iZkZlb8xffWSggXLWKb+O8YslM3pOPmS/OOISBEi+pg1bjLQQGySkXuC/jFwVF62twvp3ZzjDMhPpW5/nBiucEkM6rufupwhTta/DCmxQx/fW/wAY0471owbmCbmaxkEINBv7vAZehdXxOdMIgQpckA8e2E7MjKDnTmBNbl9IAqFRZIjumB6In1xHYdlUnEPAhT04X1FMrlFT39jITsE5rDwphOzwxygKMHnH0gqhDM/j64/FIXA/DJkVDhnYHAEI3vxgOBVMNfjTiGTIp1N8vZuNvEVCdFsm6jxFHpmwyIJsvKs99m8aITiBoGxkw1hPALiUX4yWwWgdusossAeN/LR5xTgwhQ3yayFQiTJf49sZRJgt7CPzvKTWdNN+MSZPIRQ9fxghsEAUT5nxkmMWmgbj9YkCMF1WQjQtGNQ7xIa+Vmb/AOfy1iOSSWg2H9vxgK0FsmWe3Gz0rHx9M1BIMXlVomQk7/3Ajunh6Zv8e+UmRgzqfnLeA3/FkhJImKR8MYGChNzFW97xQnWUo5+fGGXiOSHXGCQt0GDDfJirzFV3H/Y+uBHiJdBbiO6wcFyJJkT0CjxOKJEKGiirwwioEcr/AJN5WS2akBZ+MXWrFMspb8/elsjSjIWab7wCZUil+E75jznYBalVCf6+MBStGWkEpv8A4ecGpyXKxaX+MRIIig61ZB/GPlCQkk7kV9Ned7zkEYB0fP77wjFEAgqWPxGcECErvn84EgDpfx/OGwwCpdff1koBDsCCe8SRSUbidN+KyrKdGGxZ54x9yHt19rElO0Sfv7vB9J5nGiVq5E41BCp3dfecUBKX/GIEosGiOsCshA1BPtkyiQZ4jTXvjkJIZNxNx91rDTRT8JZ/B46wxdVstXHOQENEcfB95yEkWMq+4PLxjqqn8F84vaCgNiOTfH5yCtwXIeI7wyQTaLc5CRB4gNfOSFTCSDwagqG+/Ry+TjoMIAINQnZ3xlQBY2Ddek5YVUSzGka11eTtIIoZhl0/vNb9QQ+vv/EZAsmyOgNYoikgoI/nvrHBYLQUGjXmP59NBc4otrfp8E4MBLDUKRZ7V5y47hIXidIcvRr1xqzTtcfxP8YkASQI/N86xmKnQWNvOKQKlG3r98Yp0I7R9/OIomaIn85CrQ6GsYJ4Oo+0Y4EuskGn11kxMmaH2f8AuKwCSFQLrBaCGCV2/wDcag7XRDxHOBdCkcIOq9vjGdsIkI6xQyGDYY9/XLNcCansnjJojclyczgjcugLrr1jFJUmJHP94oiRhnH2P1nCmEtpezycY4qZJsSTRZqSNcYQTpEglvOMCjgZamJ55ofLbz6RjzxNG1WhPWNdZX3tQnr+cUCA9ds/784DQDCBAgE/jGCRpGODFjAqIO7571jo7auz0yQL5C51x7Y0tjp2q7MYICNx3ckRqOP8x2AQCGSDH+ZDVozXvjz/ALlxba2nADDez5j19cRoPk3x998iA3XDjFFxHb84KhQcE5ClKCZ7vBSONImfjFECES95ZL5U/nFzAYPxlsQcjgyULBpSljUBedk8YKR2IXPz+MlqRFgo8/lxBKekgefv95XevgTiUlNuy8kJgCqnVEg+n785BBgSUFPbf2O8nGMlEr98YLsBQDAFR99MQ0YW60+fj85AikbjJtAKN59nFvIJioVPGDJUFS+3eSCNNr3DZ8TkkAxDc1KRHuOLEQpkCfXAL1Q1P9YtCQsoDB7cemMKhSOznxg5MxU4EVRd8p9/bgilLFJy4KNiQS171eIyBVsEq5nDkzjQkR1xg8UFzZhYGq45bwvJUzK1wT984CLB3VYUi1+N4Bl0aB358fGLBwDap+1/zACGzrE0ko9mow2I9JjCAY9I8x/zEXMFtyxRNCHOAXlhLvlFe+SglhBGDIwBJM+ZPf4xqaLY3sqMSRROxb3qMMkr2ER7r+DFOSFSJNN7P3hD6UwQ+TCCwyaiMMIEIjUG/wB7yUACOJf3iVcs3S33/WECSGWZiD59PfIgMPoMcp7tYswAq2U6iJxkUNkXpyDghsH0nBVO03qRNYBFSZVHjCwxV2LkCpkEhiWc1oFcNen4yJtNjEoev3WBpPZgX3Yltn9/GIpigwsd/NvyZPNqqDVH9ZZGBsrbCEqEkjiWixdfe8WcmcIIIrdyfjCkUO4vIIiIiZJxgJCZ24JZJXnEKCQPoPjBARgCDcF4sYBFqU4iGAIEo/POICERGtfZcFRuJCp7fzgiUGgYkPTXn8YhcNScORFp5V+8Z0SvB75NKPVH5xNPfbGMiUbJdYgTdXWZCutmRpLRWL5n3xU2DASuZvFGUUxVYAxAEp2R6eMsApJDOiMQwhDaKywQgSkZCOkhkpOt94kiKSzf5+MVpARL2cYhkFILO8aDS0R99cDtuzZjSyVVofr1+cViIARXjGXaxzYAFd43VHOEQIJsq/WslDoINly8syneI5xNRjRBANVkcFQ4wzbNHEYPBmCh+8dromSnpkkLRo98nZGlx5yZk3K/OKgMMZMSswnGQ3EuPzhRWDUOMlJRVPJMcVioJIgXUde2B5u8/9k=\n",
      "text/plain": [
       "<IPython.core.display.Image object>"
      ]
     },
     "execution_count": 274,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "IPython.display.Image(\"/home/sam1902/Pictures/WandererAboveTheSeaOfFogResized.jpg\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 256,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Image original size:  (1399, 1100)\n",
      "Resampling factor (2.073624017155111, 2.090909090909091)\n",
      "Image resized : (2901, 2300)\n",
      "Max intensity:  1.0\n",
      "Min intensity:  0.0\n"
     ]
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAD8CAYAAAB+UHOxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJztnX3MX0eV37+HEAeVYGE3reUniZts6gKmKyepFVtagooCcWIqmfyDgqrF6yJ5pU0qqLZqzW6lRWwrpaiwAolG6wi7ToXIImBFRNP1OhGrdaV1iBPFeSVrb8gm8WNiLY5wEFJe4PSP373OPON5ve8v34/06Lm/uffOnTv33nNmzpwzI6oKQggh8+MdfReAEEJIP1ABEELITKECIISQmUIFQAghM4UKgBBCZgoVACGEzBQqAEIImSlUAIQQMlOoAAghZKa8s+8ChFgll+i78O6+i0EIIaPiNbz6D6r6T2LHDVoBrH7/e3Ddcx9ZkbZ0dDWWt53rqUSEEDJ8HtTv/H3KcYM2Ab3x419fkEbhTwghzTBoBUAIIaQ9RqsAlo6u7rsIhBAyakarAGgKIoSQegxaAax6/6CLRwgho2bQEtY1CEwIIaQZBq0ACCGEtAcVACGEzBQqAEIImSlUAIQQMlOoAAghZKZQARBCyEyhAiCEkJlCBUAIITOFCoAQQmYKFQAhhMwUKgBCCJkpVACEEDJTqAAIIWSmUAEQQshMoQIghJCZQgVACCEzhQqAEEJmChUAIYTMFCoAQgiZKVEFICJXisgPReQZEXlaRD5bpH9BRE6JyOPF3w7jnM+LyEkReU5EthvptxRpJ0Vkbzu3RAghJIV3JhzzFoDfV9XHROQ9AB4VkcPFvj9R1f9hHiwimwDcDuCDAJYAPCgi/6LY/XUAHwPwMoBHROR+VX2miRshhBCSR1QBqOppAKeL7ddE5FkAlwdO2QngPlV9HcBPROQkgBuKfSdV9XkAEJH7imOpAAghpAeyxgBE5CoA1wF4uEi6U0SeEJH9IrKmSLscwEvGaS8Xab50+xp7ROSYiBx7E6/nFI8QQkgGyQpARC4F8F0An1PVcwDuBnANgGux6CF8uYkCqeo+Vd2iqlsuxiVNZEkIIcRByhgARORiLIT/N1X1ewCgqq8Y++8B8IPi5ykAVxqnX1GkIZBOCCGkY1K8gATANwA8q6pfMdLXG4fdBuCpYvt+ALeLyCUicjWAjQB+BOARABtF5GoRWYXFQPH9zdwGIYSQXFJ6AL8F4LcBPCkijxdpfwDgUyJyLQAF8AKA3wUAVX1aRL6NxeDuWwDuUNVfAYCI3AngEICLAOxX1acbvBdCCCEZiKr2XQYvq2WtbpWb+i4GIYSMigf1O4+q6pbYcYwEJoSQmUIFQAghM4UKgBBCZgoVACGEzBQqAEIImSlUAIQQMlOoAAghZKZQARBCyEyhAiCEkJlCBUAIITOFCoAQQmYKFQAhhMwUKgBCCJkpVACEEDJTqAAIIWSmUAEQQshMoQIghJCZQgVACCEzhQqAEEJmChUAIYTMFCoAQgiZKVQAhBAyU6gACCFkplABEELITKECIISQmUIFQAghM4UKgBBCZgoVACGEzJSoAhCRK0XkhyLyjIg8LSKfLdLXishhETlR/F9TpIuIfE1ETorIEyJyvZHXruL4EyKyq73bIoQQEiOlB/AWgN9X1U0AtgG4Q0Q2AdgL4CFV3QjgoeI3ANwKYGPxtwfA3cBCYQD4IwBbAdwA4I9KpUEIIaR7ogpAVU+r6mPF9msAngVwOYCdAA4Whx0E8IlieyeAe3XBUQDvFZH1ALYDOKyqZ1X1VQCHAdzS6N0QQghJJmsMQESuAnAdgIcBrFPV08WunwJYV2xfDuAl47SXizRfOiGEkB5IVgAicimA7wL4nKqeM/epqgLQJgokIntE5JiIHHsTrzeRJSGEEAdJCkBELsZC+H9TVb9XJL9SmHZQ/D9TpJ8CcKVx+hVFmi99Baq6T1W3qOqWi3FJzr0QQgjJIMULSAB8A8CzqvoVY9f9AEpPnl0Avm+kf7rwBtoG4OeFqegQgJtFZE0x+HtzkUYIIaQH3plwzG8B+G0AT4rI40XaHwC4C8C3ReQzAP4ewCeLfQ8A2AHgJIBfAtgNAKp6VkT+GMAjxXFfVNWzjdwFIYSQbGRhvh8mq2WtbpWb+i4GIYSMigf1O4+q6pbYcYwEJoSQmZJiAiKEFCwdXb3i9/K2c54jCRk+VACEOLAFvcmBDUew+8UbncdRIZAxQRMQIVgpyG2hfmDDkRX/d7944/ltMx0ADi0fx9LR1ef/CBkyVACE4O2Wu09om61+WyGEtgkZMlQAhBQsHV19gQnHFuamIrB/mz0EQsYAFQAhBcvbzjmVgC3gbVxKosyPkCHDQWBCDHzC37VtC35zP4U/GQMMBCPEg2swOMW84+tJENIVDAQjpGFipiATCn8yBqgACMkk1Aug4CdjggqAEA+lMI8J9eVt587/ETImRjEITHsq6ZNDy8edg77nWV75c/vS5vYLRQgCEetb084fhQLIEf5UFqQpDi0fP7+dGty1+8UbsXR0sc33kISwZZVLmLv2u4IWTceDnAj0QSuAVe9/B5YOXjjXiq+iyvRYRZbYFUpI+U74pn2IseLY5cX5fL8IsFLehKYesb3I7P0u+RaSfSEG7QZ62Qcu048f3Jl9XkxJpH6QPg1r7revZedtP3QKg2Hhm/enLagQ5k1X80Pdu3V/khvoJBWAj9zuUVtCO9TzoJJol64Ffggqg2kxpMn/JqMArnvuI9lT7rqEaMrDyVUQKeSOX1Q5j8SxTTtDhoPI48FnvumbSSgAOxK4idZxUy3s3IfsMh3ZeZk2P3tQhwqhOmMS/uaYAxXBcBiCUE9ledu55EjgUSmANnEN0PhG1tvS8qGBat9+EmZMwt+E5qFhMHTB73tHqABaps0Xgx9+M5jPaGwKAJhnDyDmEdNE/rG1H5qkyWvl1AEVwIAJ+fP6oFKoxtLR1aMU/iVTUwK2ALZ73HXyM9O6wlfmJrwQ65CqAAYdBzBV7BeAwr0dxi78gXF5hfnK6ksPTbURuu8Uv/g2yHkOvmOH9iypAAghQVKVUMixwZePb2ytamRrFWKxPFOGJiAyWcY6AOxizKagmKtkTpR+yGxEr7m34RgAmT19m4Byp5GI5TV3oUbS4YIwZNYMwX2vSeVzYMORFZPTEdIEVACEjAgqAdIkVABkcozB9r99aXNluz6VAGmKqAIQkf0ickZEnjLSviAip0Tk8eJvh7Hv8yJyUkSeE5HtRvotRdpJEdnb/K0QMnx2v3jjCsG/+8Ubkxaat6ESIE2Q0gP4XwBucaT/iapeW/w9AAAisgnA7QA+WJzzP0XkIhG5CMDXAdwKYBOATxXHjoalo6sHYVcm06JcSrJUAjnKgO8jqUtUAajqXwM4m5jfTgD3qerrqvoTACcB3FD8nVTV51X1DQD3FceOAlfkLj++YZNr/slthdvHp5wf8uQp0w9sOFKpR0BIFeqMAdwpIk8UJqI1RdrlAF4yjnm5SPOlX4CI7BGRYyJy7E28XqN4zcEFv8dDVcVsKowUAWwrmBSFEztm+9LmLOFPzyBSl6oK4G4A1wC4FsBpAF9uqkCquk9Vt6jqlotxSVPZNgoVwjBxCf8qremc9X99v33XTRHYZS8gpexjDhAj/VNpKghVfaXcFpF7APyg+HkKwJXGoVcUaQikE9IoVdfzrXod1+/QdUNz5gBp5WZgGGmCSj0AEVlv/LwNQOkhdD+A20XkEhG5GsBGAD8C8AiAjSJytYiswmKg+P7qxSYkTNvC37yO+T+FAxuOeE1VBzYcGbT7KpkWKW6g3wLwNwDeJyIvi8hnAHxJRJ4UkScAfATAfwAAVX0awLcBPAPgLwDcoaq/UtW3ANwJ4BCAZwF8uziWkEYphWeuTd/GNuf48nBdL5fSqSA1j+1Lm2fb+jcdMOiIUR/OBUQmQxdz/zTds9i+tDlb+M+Z3PXB5wrnAiKkBZoQ/mZv4tDy8aQ87QCyIWC7Q4da5OWxKa320DGmwKfwrw/XAyCToivbfx1yylcqi66EXUz4xqZ2LvOosxRi7F4p+JuDCsCCc4mPmyEJ/7rKqGtPn5hwjwlz14Iwdl6pS0C61gtI7RmQdKgADDioRJqkqvAvW/0HNhzBdvRn9kkRuL61b0Pn5K7hy++yPWY7BmC3bOosTE2mh8/rxxfsVXf6BtOdtAw07Nrmbwc4htbstc/J/W5yxgRy82sjz6kyOy8gX4ulzeXkYoE/ZjlIdfpeAawuXQp835KMKcIup/Xfl/Bs4lvK6d0MjVQvIJqAClJaO7nE7Kec+Iv0hWmL9y3M7iPm7ZNLG99BlUXe7YZa7LwprEE8SxOQKezbeHCxbmMZ7Wm/9FPuanbB2BVql89/SO9a288s1YyTKwvaaDR2zSwVQJsa23zRfOaI2ERfU7c7tsEYVgGL0WbZc/z1xyzQQsS+K9/+JscChvZdz3IMoM4LHjo/NL+Liyotn7ZMVLn5D8k+OqUpkdt0/Rya8OmLKgPWPtNYSl59KFVGAnuo+yBSBnOBlZN6lS1+W+CHJv6y95XbdVsidVszrnP7nB67C6HmUtRjMTWZz7uPZ9TVNXN6T7nvTMhkbH9PvnGVoTLZHkAXL3zpdWL6bbuoGhBUnmf/N/entkBKTKWUguuFt23toR5Rm8/AdN1tsxdg1nvus6zy7NsOAEsVgCkDwnWO7xOfJ1NOvQ+pF2yT2gOYrAJok5id3xau5YeRK0RcisWVd2pZzTLbQs13nRS3vipBQU2QMt5Shz6nlXApgaYUqqk4U1qqYxHqOcTeWZdn1FCEewp0A8WFa/k2lR+QNt3weQF79EanOccm1pMo9+WaH1y9B1e5zWPKc1Jf/D6EhK1Ym6ZP4W9TVQC5voGqro5jIHUOopxekPl/agy+B3Dbw7ddkB6bQ6SNQC4Tl9knJpRzlhl05RkS3rH68CkA17XN67mu4aoL1/kmbQ9qtiWo+55Ybkirfg1ZAdSZeM6Xny82YijPI8YkBoFXvf/t4qWEnJvCv6nQcLvVb7aQ7bVbXftDCsK1mlRbYwo+BRJSMuZvVz2mlqGN0PwuBFLfLqVdXz9Up20KPt93bX/z5u82HQ/serBdaIesDHMZdA/gsg9cph8/uDN4TI6NOhfXIG9dYe073hzotYmNM6T0AHKIjT2E8vPVVaycOfjGNZqg71a/zRDXALAJecbVcZ+sShcC2mxoDrFXMIkegE2OPa6pVkJIoJX4BLRPmLuOTzXTuK7pe+HL9CpjBnbvxiQ1P/te6n6Ydje8jQ+v7lKSTVKOwXRNrCeQMoYQa9VXuXYKbdWXr+cxROGfwyh7ADkvUB1N7TN5xFrpIQ8b32BsTms71FsIlSuH3LxdMQ6ufXU/mDqt/y5cOJuird5T1wythZw7+DtWJu0FVGVApk6EK7BSyIQGZF0++zEh4rO9h4RwaF+ur39Ovi7PoZxr5z67WGt06ejqZEEdUqapx6eQUp7tS5uDsQsHNhw5v17wmBmaIG2z9zFGRtkDKIn5LdcJ6vC16M3fKW6bJqmt/1DeKYLfPrbqGEAuMfdWF018kLnms6Fj2/2H1oomw2cSPYA3fvzrC9JSfJJzPxa7JRYyZ9i/YwO0uT7/pjCLtbZDZQxdOzVPH7FnkDJu0nT0cF0lZ5/vGnw135MURZ1TpthgL5UAaYNBKwDgwsUqmu6mxWzKKSYCW+CHhLdPOfiCsuoORIZ6Abl524NfoWcR8p4Cmp9Tvi4X1sWFwnalkD5XLNforoecXqHveiVjCsQi42JUXkBA+5F5sZah63jT59/2nCl/Vx0HyBck6fcQyjvX59ruFYXKE7pGFc8tl3L1HdMWuflvX9qM7Uubs+6XSoA0zaDHALqYC8gXTVrVphzyEHK1/psQTLE4g5TxhDrTDOSSEruRQ1XPHtcga9V6CHl5uaji3z+2aFTSH5wMLhFbAdgunLEAryoCPMeFs66CcA2QNuliWFcJpEzGFaPq4G8phOvY16tMSFc1uIsKgKQyyUCwJsiZSsAlNFMGOM1z69jemzJbmAqtDf/yXPNNLEAo11fbF7AWwgyyakr4t21mouAnTTP4QeCmiM5zslwtYtZ3Topd2lWOlPlY7DmPqg4SNiX8Y+mxSOVY/r6JuepMB1362cfIaSjEpsgo96fed6hMVAakCaImIBHZD+DfADijqv+ySFsL4M8AXAXgBQCfVNVXRUQAfBXADgC/BPA7qvpYcc4uAP+lyPa/qurBWOHqLgiTg8/s44rqbQtfC7huBHPoWm1TxcQTqge71V51RtDdL8Zn2kzxcsqNQajjeWWXi0qA+GhsDEBEPgzgFwDuNRTAlwCcVdW7RGQvgDWq+p9FZAeAf4+FAtgK4KuqurVQGMcAbAGgAB4F8K9U9dXQtasogDoDiikfcx0lEBJ8bU6U1sZ1ckiJ5k0R+r5z2xD+rrKUpLoJp5QjBd+gORUA8dHoILCIXAXgB4YCeA7Av1bV0yKyHsBfqer7RORPi+1vmceVf6r6u0X6iuN8pCqAobjH5QY+tbl2wZCFg+u+cwS/eUx5bq4QDpl/Uv366wp/XyCZb5zJZVYb8nMm/dF2JPA6VT1dbP8UwLpi+3IALxnHvVyk+dIrUdXE0aSisAVUzKc+J71uuYaObxA4Ja1tciOcq063ERs3cEWED6WhQ6ZDbS8gXXQhGvMlFZE9InJMRI69idcv8NhJsY+nCg7XcWVAV8p5pueK6YlSJ6iJVKOp8RnzedlC2n43Ut6VVELxI2agoZ0+tQVKSLdU7QG8IiLrDRPQmSL9FIArjeOuKNJOYWEGMtP/ypWxqu4DsA9YTAaXIuDrCHwbU4inQiE/DJoOwsqdeymnDKH8UqLPbWgSIlWo2gO4H8CuYnsXgO8b6Z+WBdsA/LwwFR0CcLOIrBGRNQBuLtKC+CaDI8SkfCfqTH6XEx9SRTG4zou5ELvSXL0Qk5z7ICSqAETkWwD+BsD7RORlEfkMgLsAfExETgD4aPEbAB4A8DyAkwDuAfB7AKCqZwH8MYBHir8vFmm908RcNKQd+7Tp7x/LP7XV7TrONZYTmjajKr6ZX1PKGPI88t07FQGJEVUAqvopVV2vqher6hWq+g1V/Zmq3qSqG1X1o6Uw1wV3qOo1qvqbqnrMyGe/qv7z4u9AmzdFusElXGyhnTvrpyvIy9znS08NvHOZf2yF77L5N2XrL7EHj2PlrzOPFBUB8TH7uYBIOnWijkO4XEJ91wlNrZFiOw95h9nBgClzQeWSGzSWGl2cE7DIHu704WRwJEhqDEKTQr9KPrbve50gLN/gb24cQd2ZYmNRxE3kb/42r2lDZTBNqABIEN8UDb59LuxAppzIVp87b5uzgPo8vHKnk6gioFMjzHMVUegc34y1LgVBRTAtOBsoceKyB5vCN6VnUNrGXYu+pPjG59j37TKaVJkFtLzWoeXjndrGUwR7rm0/ZA5zDRSHZoXtuj7IMGAPYCZUadXnHOuKXA2dZxJbr8CHqyfRpCknZ3GdWN5Nmo1i+bmOc/XUbIVj/2avYLzQBDRzQhOs2aSaCUrqjgnY1/PNieO7fq6SqoJPwFad+iGUZ5PXSC2DT+naaVQC44QKgARns4x5uoQGFO08fOf48rTzcF0ntYWdMrAaUiKxlrV9TJ0J4KrQxIRzvn0lvjo7sCFtzQQf9joOpDuoAGaOz4XS5U9uk+NeWHUguClh6rteW63n3LxTA73qlMmnwFNMUC4FZ5axjgIg/dH2bKBkwLgiW3OFVykQ7IFEV4vddYzruqaQqduydVHXZBMrU46CC5Uv1ZZf7g/ll1qHKQrXVVdcfWzaUAFMjNR1alOEnesce59LsKQqhxg+RZI7EJp7rdAxVchVHCnjHqFxm1A5fGm+Z3Ngw5Hzy6WGTEJ9TkbX9iJLU4YmoAlSBjbV9TwB4tGxVXsWbQhou+w55Uq5dlMmq5SxF8Bd96mk9jBSymqzfWmzM0DQtWZ1Dr61rrk+cj40Ac2Y5W3nsB2bsXR08buKS6Jvf6gVmULT9u8urmW2klPxmXlceVUxPYVMe/axqUoxNt5Tcmj5OHa/eOMFLe+6vQBbofjmhTLzp/CvB3sAE6fOoum5SiOUV5UyxPJ0Cavcge2q12zqnNiYii8v38C7a5ymTVyKwieUq7gOU8BXg15AZAWpy1cCzZo8zPxiaTnnluSUs045co+tcn7MLNRkHTZN1fGRFDMPyYcKgDjxRc6muhMOnZzB3LbuK0Vg57ppNl2+XGXS9CD5nAV/FwPmVAAkSMoUyG32ALqi7VZ7Hfo03TRNrvA3iQWMTWm5S9+9hCZnrAIngyON0pT/e1PXMo+p6uqakkeTrd7yWNul1RwYHoPwr/MuACsXC3INJPv2j32iutACSH0pN3oBzQzfWEAd756mW8kpecXK3sQ1Xd4zvpgHF75jhy7kU72SYvVRZ1xgSsQEfxXFFvKMyoEmoIngs6eGXq4c75Q6jG0cAejOxdS83tjqqCQ0KJ+qBKYm9F2kCPrcb9hXb4wDGCGuVkEsCCYlrQpdt+iHQCzgqqpwSxlTGVId5XqB2cfYv2Oz0s5B+Ifo8/7ZA+iRHGFdZcWsGEMSOj7q+t5XiTgGwu6lVRXEGOrbR6oXUCiGYe6C3qbqsqy+XoKZTi+gAdLWoupNMUQB1Ubwlet4m5jgt712XL2HNuqzK8+spmJB7PM5u+iFpE57kQMVwMDoS+indL/NFzA0wDc2unLhLKnTQh4SbZWzzNdWAqnfBnsQ6VAB9IDdwi9fdt+Iv/lC11UQuWMFoXD9oQqpvgSorRCrmHbGIvybJteMVhcqiQWMA+gBe5KqsqWzvO3c+X3ldsqLGpv0Kicvm9LHulwM3MyzrY+zLm143pj/fce4TDu2D3/sGnMl5k5qx0D4XGVTYyTKd7r8M9/xoZpe+2R2PYC+Ay/6ILQ6WMxve0qt1ipjAz6voFwT2ZijfJsmZGJ0DeDbz8EVNR0bmPf9BqYpC9gDMLCjCqf4wGO4ok1D7nupZo2c9LbIdcdMxa6nmLtjLK9cZTFVQsoz9R30PQu7J5GipOfcM5hND6DpuTbGhDkm4WqJhlqnbXu1dEHVln9KHk1MokYWtO18EOvxDmE1s6a8gTgI7CA26dRUqbomQEkbE8TVLQchdXHFbKTKhbpCuu2guE4UgIi8AOA1AL8C8JaqbhGRtQD+DMBVAF4A8ElVfVVEBMBXAewA8EsAv6Oqj4Xyr6sA5mzyMYkpgDnap6lMiItQnELVqRxitCGnuhwD+IiqXmtcbC+Ah1R1I4CHit8AcCuAjcXfHgB3N3DtIFU9ZOaCPSvlnLBbfl3Z3adu3x8zTQSphWY69dGnnGpjEHgngIPF9kEAnzDS79UFRwG8V0TWt3B9YlG+YL7ZLcs/k6EO5DZNis25ybI1qWipTJojVpdVB4pzlUHX+dedDE4B/KWIKIA/VdV9ANap6uli/08BrCu2LwfwknHuy0XaaSMNIrIHix4C3oV/dMEFq9rebPv/HM1Dy9vOYffRleaeubX8XcTqwDd43jdDKkvXNGnCOx+hDHcPwLWKnsslNUaVWT1T86sqx+oqgA+p6ikR+acADovIj82dqqqFckimUCL7gMUYgLmvCeHv+j0EulBI5jVKRVDStzDp+/o+SuEw1PLNldB4VlV331SqzAgbwyeTSgXjCwQNnZtCLROQqp4q/p8B8OcAbgDwSmnaKf6fKQ4/BeBK4/QrirRkcoRjqFtUJ4I2h/L6rlWOQqseNdVttK9vpudEs3bFEO3wfddNLEqZrKRqrIWvLg8tH3fmb/cIfd+TL+4mFI9jc2DDkcZ7DyWVvYBE5N0A3qGqrxXbhwF8EcBNAH6mqneJyF4Aa1X1P4nIxwHciYUX0FYAX1PVG0LXSPUCcs2yOQSf3qrY3cqq9+Jb/avpGR7nwBBNQKRZ7JZ2yPRjptl5hMxCKZHlocjnVFnQhRfQOgD/T0SOA/gRgP+jqn8B4C4AHxOREwA+WvwGgAcAPA/gJIB7APxejWsDeLtlW2WenVi+uWVochI1W8DGegP2fCf28XUiWF1MXQiag+JDDIRjy78b7Na8+V26TECudyXUA7DzSYmMbtp8XVkBqOrzqrq5+Pugqv63Iv1nqnqTqm5U1Y+q6tkiXVX1DlW9RlV/U1WP5VzPZxZpo6WfukhD3QArG1+UYpnuMunYisfuitYJ/qqzv27+Xeflmuyt3Db/N3WNOufFIraHxBjKVSp806Zemn5c0cOuVrxLEficB8z02Pxbbdff4OcCcrXyS/ry4DEFvykgQmYCV4vAxn7ZXMeVL+aBDUdwaPl49Hgz7xzant6gydZ0VbuvL4+2Prqq95xy3lB6JyZDMxWaQtf1vboamC4bvy9f33cfEvKxBoZLWTTZC5jVVBC5xEbmYy12G1/rwZWfK99Q3qQ/2pgnyNfybIM28h6a8A+RUteub9f+bm1FkDOFis+zyJWW0vDlXECJxIS8Kx0Idw3tY2LHpn4srpaGr/WRmzfpjqrPhM+yPn0qO1+j0dUbcckI00QVWlp2eds5KgAfIYFfEjMBhLR6rDWR8wK20bIk/cJnMw1SnqOvwZZiqnXJFRc++XDv1v1UADauNW9LYt07k5wuY7ntu06Z5svHzi/1xaOQIeRChvhttFGmi9af4IIwJqa3jGvg1PUQqnTr7DRTo8cGgm3l4HMrS2WoHhiE2HT1rg5N+AP9lmkWPQDbVTLW0nbRls02RYGkDiQ1TcrA9hgZYiuQ+OHzyoc9gAAhe7+vl1D6Cle9jutavhfbJ/C7+ghcvZYm8hsKFCbdU+cdyHGQIHnMogdwaPl48uCLTYrdfSgtlC7GB/q616HUMXmbLl1Vx0ifvXf2AAqWjq5OqvyytWv/lft8+Hz7zf0hqrRcXOMEPlOSvd2n8G+7FUi6JXXMzPXcx9Ri943Lxagr/Luoo8krAKDZCNmYyci3v+r1XLjMQin3mHPtUAxE7DgfFOLzJGTmrEqXCqSuGTbXhFWam3NkR9X6mJQJyJwywpyuoc3uV1Vf/dR8mxiIbeL+p9K9b+uEdH2nAAAGjElEQVQ+plI/qcztfpsk1htvwnQ0eROQa2K0MjrOnO8+pfuZqj3tgeC2hT9w4RwkdXssQ6HqM6hLW0JrbsJwivdbpadcBft79smULpTsaHsAsYjeJgKnqjyAIbaMhlgmQuZOk9+lnVdqD2A0CiA0A15ucFRTGnYugrWp+xxTfY2prGQ8dOVROBkFcNvDtwHwT3bm++0ip6XflnmH5MH6JkMhxZOuzvuaI4diTEIBbNn8Lv3gPf92hS0/dUQ9ZYAlZT8FUBqsJ9IXfPcuZBKDwC+8cWmSm6NNSqSvb38orynR9EDXVOuJDJ9cE3BO+tQZtAK4atUvVvxuwwc3NZhlajC8nkyJ1Hc1NV4nNe8qU8Sk5NsVg1YAL7xxae08hlDJY6VJZTiV5zCV+5gaKeN/5v+qFgU7vzrfyBAam4NWAFet+kXlMOySIVRyFaYmaNoMxOuSsb5Pc6eKKTklvxSaekfbeNcHrQCA+mHYY2VO95qC7+UfQz1NTZn3SU7QZpvXz4nQ70PppDJoBVDHBNTGJGykeVInCmtyPqeuCU0WSPIo67IP5w07Qt9MHyuDdgO97AOX6Zkfru27GKRFUl34mj6OkLp09a5Vuc4k4gCoAKYNhTUhaeR+K5OIA7DdQKfOmLuSVagyz5Jrm5A6jOFdaquhNGgFUIeuZvZrki5bw2Oql5K5OgTMiTbfyzE7ErTFqBVA6GVp2u1ragytXqq27seoyIifNt/Lob3zQ6BzBSAit4jIcyJyUkT21slrTJ4hQyvP0KjauudHTUz4neXRqQIQkYsAfB3ArQA2AfiUiGyqklcsPHtogmFo5Rk7/NCJi7F+Z32ZrLvuAdwA4KSqPq+qbwC4D8DOKhmN9UGTZuDz7xcq4Gbpy2TdtQK4HMBLxu+Xi7RGSZ0XpCn4MZCpkDupGhk37+y7ADYisgfAnuLn6xetP/FU81c5gXsHnV8WlwH4h/4uPwpYR3GKOur1XR46Y3qP/lnKQV0rgFMArjR+X1GknUdV9wHYBwAiciwlmGHOsI7isI7isI7iTLGOujYBPQJgo4hcLSKrANwO4P6Oy0AIIQQd9wBU9S0RuRPAIQAXAdivqk93WQZCCCELOh8DUNUHADyQePi+NssyEVhHcVhHcVhHcSZXR4OeDI4QQkh7jHoqCEIIIdUZrAJocsqIsSMiL4jIkyLyuIgcK9LWishhETlR/F9TpIuIfK2otydE5Pp+S98OIrJfRM6IyFNGWnadiMiu4vgTIrKrj3tpA0/9fEFEThXv0eMissPY9/mifp4Tke1G+mS/QxG5UkR+KCLPiMjTIvLZIn0+75GqDu4PiwHivwPwGwBWATgOYFPf5eqxPl4AcJmV9iUAe4vtvQD+e7G9A8D/BSAAtgF4uO/yt1QnHwZwPYCnqtYJgLUAni/+rym21/R9by3WzxcA/EfHsZuKb+wSAFcX395FU/8OAawHcH2x/R4Af1vUxWzeo6H2ABqbMmLC7ARwsNg+COATRvq9uuAogPeKyPo+CtgmqvrXAM5aybl1sh3AYVU9q6qvAjgM4Jb2S98+nvrxsRPAfar6uqr+BMBJLL7BSX+HqnpaVR8rtl8D8CwWMxPM5j0aqgLoZMqIEaEA/lJEHi0ipQFgnaqeLrZ/CmBdsT3nusutkznW1Z2F+WJ/adoA6wcichWA6wA8jBm9R0NVAGQlH1LV67GYRfUOEfmwuVMX/VC6cxmwTpzcDeAaANcCOA3gy/0WZxiIyKUAvgvgc6p6ztw39fdoqAogOmXEnFDVU8X/MwD+HIuu+Sulaaf4f6Y4fM51l1sns6orVX1FVX+lqr8GcA8W7xEw4/oRkYuxEP7fVNXvFcmzeY+GqgA4ZUSBiLxbRN5TbgO4GcBTWNRH6W2wC8D3i+37AXy68FjYBuDnRnd26uTWySEAN4vImsIccnORNkmssaDbsHiPgEX93C4il4jI1QA2AvgRJv4diogA+AaAZ1X1K8au+bxHfY9C+/6wGHH/Wyy8EP6w7/L0WA+/gYX3xXEAT5d1AeAfA3gIwAkADwJYW6QLFovu/B2AJwFs6fseWqqXb2FhxngTC5vrZ6rUCYB/h8Wg50kAu/u+r5br538X9/8EFsJsvXH8Hxb18xyAW430yX6HAD6EhXnnCQCPF3875vQeMRKYEEJmylBNQIQQQlqGCoAQQmYKFQAhhMwUKgBCCJkpVACEEDJTqAAIIWSmUAEQQshMoQIghJCZ8v8BhOehAEpWXwYAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x7f88cfb604a8>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "imgMat = loadPicture(size=(2901,2300), file=\"/home/sam1902/Pictures/WandererAboveTheSeaOfFog.jpg\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Generate spectrogram from image\n",
    "The spectrogram is a graph representing the frequencies and their intensity relative to the progress of the sound. It can be obtained by computing the Fourier Transform of the sound at each soundframe.\n",
    "\n",
    "Therefore, to craft a sound that'll render the desired spectrogram we have to play a set of different sound which each individual frequency is related to the position of the pixel in the original image, and of which each intensity is related to the pixel intensity at this point.\n",
    "\n",
    "To do so, we first load the image and resize it such that each column of pixel correspond to a frame of which we've got `max_frame` amount, and each row correspond to a frequency in the `steppingSpectrum`, which is essentially the maximum frequency allowed, divided by the step between each frequency band. We can further tune the frequency range if we want our custom spectrogram to appear more up or down the frequency spectrum, but for now lets just use the full spectrum.\n",
    "\n",
    "Then, we multiply each pixel value (which was previously scaled between 0 and 1) by the `max_intensity` so that each pixel value is now the intensity of the pure sound to play.\n",
    "\n",
    "Finally, we compute each soundframe by iterating through each column of the image and, for each pixel in it (which correspond each to a distinct band of frequencies) we add to the value of the sound value of that frame the sound of the pure wave corresponding to this range of frequencies, but we walk across these frequencies in substep of 1000 Hz. Strangely, the higher is this number the less \"spaced\" the drawing appears on the spectrogram. You can try lowering it to see what I mean.\n",
    "\n",
    "Then, after iterating though each pixel we divide the sum of their values by the amount of individual values summed (divide once to avoid high computational cost). To conclude, we write this value as the frame's value and go to the next frame.\n",
    "\n",
    "By doing that for every column of pixel, we can recreate the image in the spectrogram. Tadaaaa.\n",
    "\n",
    "---\n",
    "\n",
    "###Addendum\n",
    "\n",
    "Except as it turns out, we should theoretically run into a pretty big problem which has a sweet name: the uncertainty principle. Except for some reason we don't, which is strange and I haven't found out why yet.\n",
    "\n",
    "The fact is that spectrogram is computed by decomposing the sum of frequency that make a soundframe, but if that sum of frequency variates a lot between the current soundframe and the next, it's hard to tell what were the frequency in the current frame. This is called the uncertainty principle: if you can observe a wave for a very short amount of time, you cannot accurately tell which frequencies it was made of (uncertain) and when you observe it for long enough (a.k.a. stays the same for long enough) you can tell more accurately.\n",
    "\n",
    "Therefore, to \"solve\" the problem that the uncertainty principle creates, we have to extend the periode during which we keep the same value so that the Fourier transform knows - and is certain - about which frequencies were in the sound and the spectrogram comes out crisps and clear.\n",
    "\n",
    "To do that we simply should insert the same frame repeatedly, except when I try it doesn't do as expected, which is strange \\\\\\_()_/"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 262,
   "metadata": {},
   "outputs": [],
   "source": [
    "def genSoundFromImage(file, output=\"sound.wav\", duration=5.0, sampleRate=44100.0):\n",
    "    wavef = wave.open(output,'w')\n",
    "    wavef.setnchannels(1) # mono\n",
    "    wavef.setsampwidth(2) \n",
    "    wavef.setframerate(sampleRate)\n",
    "    \n",
    "    max_frame = int(duration * sampleRate)\n",
    "    max_freq = 22000 # Hz\n",
    "    max_intensity = 32767\n",
    "    \n",
    "    stepSize = 400 # Hz\n",
    "    steppingSpectrum = int(max_freq/stepSize)\n",
    "    \n",
    "    imgMat = loadPicture((steppingSpectrum, max_frame), file, verbose=0)\n",
    "    imgMat *= max_intensity\n",
    "    print(\"Input: \", file)\n",
    "    print(\"Duration (in seconds): \", duration)\n",
    "    print(\"Sample rate: \", sampleRate)\n",
    "    print(\"Computing each soundframe sum value..\")\n",
    "    for frame in range(max_frame):\n",
    "        if frame % 60 == 0: # Only print once in a while\n",
    "            IPython.display.clear_output(wait=True)\n",
    "            print(\"Progress: ==> {:.2%}\".format(frame/max_frame), end=\"\\r\")\n",
    "        signalValue, count = 0, 0\n",
    "        for step in range(steppingSpectrum):\n",
    "            intensity = imgMat[step, frame]\n",
    "            if intensity == 0:\n",
    "                continue\n",
    "            # nextFreq is less than currentFreq\n",
    "            currentFreq = max_freq - step * stepSize\n",
    "            nextFreq = max_freq - (step+1) * stepSize\n",
    "            if nextFreq < 0: # If we're at the end of the spectrum\n",
    "                nextFreq = 0\n",
    "            for freq in range(nextFreq, currentFreq, 1000): # substep of 1000 Hz is good\n",
    "                signalValue += intensity*math.cos(freq * 2 * math.pi * float(frame) / float(sampleRate))\n",
    "                count += 1\n",
    "        if count == 0: count = 1\n",
    "        signalValue /= count\n",
    "        \n",
    "        data = struct.pack('<h', int(signalValue))\n",
    "        wavef.writeframesraw( data )\n",
    "        \n",
    "    wavef.writeframes(''.encode())\n",
    "    wavef.close()\n",
    "    print(\"\\nProgress: ==> 100%\")\n",
    "    print(\"Output: \", output)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 260,
   "metadata": {
    "scrolled": true
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Progress: ==> 99.97%\n",
      "Progress: ==> 100%\n",
      "Output:  sound.wav\n"
     ]
    }
   ],
   "source": [
    "genSoundFromImage(file=\"/home/sam1902/Pictures/WandererAboveTheSeaOfFog.jpg\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 259,
   "metadata": {
    "scrolled": true
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "File:  sound.wav\n",
      "Sample rate (Hz):  44100\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "/usr/local/lib/python3.5/dist-packages/matplotlib/axes/_axes.py:7176: RuntimeWarning: divide by zero encountered in log10\n",
      "  Z = 10. * np.log10(spec)\n"
     ]
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAD8CAYAAABpcuN4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzsvWmsb1lWH/Zbe5/zH+743qv3auiqauiRqcG03cKNY0cKxjZGliETNh9MR0JGxO04wf4Q8slRIkskUoJElBBhG9FEMcYESyClMULIjkGYoUww7Wbq6qm6uqZXb7jjfzjn7JUPa609nHP+972qTnXz8FnSe/feM+yz573G3yJmxkQTTTTRRBPtIvelrsBEE0000UR/uGk6KCaaaKKJJrqSpoNiookmmmiiK2k6KCaaaKKJJrqSpoNiookmmmiiK2k6KCaaaKKJJrqSpoNiookmmmiiK2k6KCaaaKKJJrqSpoNiookmmmiiK6n6UlfgzdLe9TnvPXkITwHnzRy4VwE3WhAYbedBxCBi4KQCdQAea0F3KrTXApgBtA5wDF8HEBiBCaF1QEdAxaiqDm3jUdUdnGNstxVAjMoHtI2XShBAPsATo+0cEAi+Dui2DtU5oT1igFi+xQAqBloCHAOB4Fog1NogzyAfACYwA0QAXbh0v5J3/KwDMxA6BzQE1BpZ3xH8WurU7QegcUDF8BeEbg5UayAcdwgbD9RBqu8YrP2AQFIOA2ACqiD3O6k7eQZvHPQpcM3SV5RF9gcCPEu/OAbWDlwz5neB7SGB5wyAQWsHnjHmn73E9m37oBYI+wFEADNJJQIBnfbRgkGO4c6lLkxAWEpf+i3Q7UkdyGt7iEGegY0Da7/Ba99XLG0M0l/2LhiglsBO+hAMwDFcHRC2HggALTrwxkufdwR4rXNLgANoQyAGwjLIN60c/Z5rgLAnY2zXqIN808bY+ppJxtczqCVQI/0Az3ArhzBnGbfGwa+lDGKgO2AgAPM7jM11vUdA0HZWZ4R2CbgG4AqgBviaZ5/Axz/3qpQfCNUl0M2B2UmHzePS59UFIei0dw3QHki7/ErmMAWgWjFCTaAAUMtoHw9w9zzaA633hQMfBFT3HZpDlj5bU1xLPA9wjoFzD/Y6x5y8F+aAn7fodJ3VJ4Tmmo6ljr13AXSnQjcDwkzWFDqbsQC1AM/knfoUaPekrtaXcf51sgaoDvq3rVmZI9QBfiN9xPsBdOEA0nJ0LVYroF1qHRwDnUtrhfU6gPq+Q7MHuFb6b3td518A5i9cYvPMPmgWUN11aA4gazcQ/AUh1DKGfg10S4a/JLjrDei1Ckxyn6614JNKlrSOz+WdF19n5lu79tYxemQPiuO37eFbf+wv4aha4ZdeeRfwUzfh/8pr8MR4/XQfVRUwq1rgozcwP2Xgr90GfeQW7v3HF2gbj/DaAmHZ4dqTZ6irDqttjfPb+6juV+ge3+LmrVPcfvkYt546wf5si8+8eBOuCnjsxjluv3RNJlYVsNjf4mC5wZ27BwjrCtceP8P9l4/wxC87vPbNjWw0r8/htoRwawt3p0a3F+BWDstXHS7fFgDH4IMWy8MN2tYhdB7Od1j8xoHcD/IuziscP3uCbeuxOp/DvzJH9+RGOuT+DNd+lxBqwvkHV8Arc3TXW1z71zOcfxnj2u8B2798H5d/cA389BoAMJs3WN1Zwh826C4r2VFaAjUE99gWs3mD9cUMvPWYHW0QPrMP6mS+N89sgJNaFh4gm8a5R3fUAjVjfrAB//4Btk+0eNc/6vC5b56jefsGvgqoP76H1dsbvPd7n8NnPvxBLF4nXHzDJaqqw3Zdw1cB7WUFf6+We1+xRb1ssPcr8v0wA06/ukF1r8LBC4T7X9cAFaPea9DeWYDnAfPjNcLzB2gea0FrDxw3cK/XCLe24NbBnVa49nuEu3+8lUXbOCxerdDsM8KM5TvLgP0nLnD54gH8pUP97jNsXjgA39wCZzXoeAvvA5p7c9B+i/knF3ANsP3aS7RntRwoDQFMcJcOey85rN6/QrfxQEeglUN9Ipsge0Z3owFah8W1NTarGvT6DOGgQ323wvIVwul7W1TXtph9bA+X79rCLTq4lxY4/gTQ7BH8hnH/T23AW4d3f6TDJ79jhuPf8wgVcPb+DTgQbv5SjXtfw1i+4rC9zli8RnjuB78PX/t9P4jTr2hRnXvc/C3G/Xc7fNn/fYI/+FtzcONw81dqbK4TmID9VwJe+0YGOuDGxxwuniLU58BjH9/i4qka9UXA/F6L2x9e4eCnjvDKnw7wxw32f2OJ1Z+8wM2fWeLlb+pAiw6L31/IoeCB5p0r7B+uwb98Hc0hsHmqgVu2OHhuibN3Blx/513cP9lHWFV45qMOL/7lNjJ8i6MNDpYb1P/HDZw/7XDx9oBw3IDOq8gELV53WL29ATrCsz8HvPoBj/qccPHeLdy8Qz1rsV3X4IsKbu0we+YCm1UNnNbAQQu+9Jjd8ZjfJxx/qsP9d3tsP3CO+a8dIMyAi3c2gGf4exVufIxw931Ad9TCHzYId+fgRSdrpXXwhw1AjMd/ZoHb7ycs7hBu/ZstPv0dkAPqssJ7//Nfxye/74NwT6/wxE8t8NKfJuDWBmFd4bFfrXDxDGF7LeDoEw7339fisd/02PtPXwH9L7dkH3ibx+IvvYrVR59AtwBu/Zstzp6u8Zs/+nc++0b320dW9TSnFvvVBgfVBjPfIdTAomoxr9p4SMzrFhSAZkmY+w6rxxzqukVVd8Jp1oy66rCoWjlU6oD2eisHQNWC6oCZ77CsZMMnz/E61QFOJY9F1YI8g+qAuuqAKqCdE6gK8FUHngWEmXKnFQDP4JrhWggXSYDTd+u6g9efFIBQIb7LFWNet5hVXfzb1UF+nwW0+4R2D/BVh1AzXN2BPRAqRjcH5nWLUDGc129UHVBLG6iS+sMzeCbPVFUHp9fruksbaC315ZqFw6kCUDHYM1DJd+u6A1fSvvvvnqPdY3jrDw+gZrzyt74R7IDLJ6UOVRXgqoCq7mSx1Iy9V6S8qu5EMiSgWwCopU9npzKOVAf4SvoEVYj9h5rBM+mjUCO2hz2j3aP4LioGO2kDz7RtFaP2HXjGYA9UlcwbVwWwtsVXAZjJXGj3Ge0Bo6qlX13dyfjqeM9OGb7q4LL2cQWwY4SFlCt93cJXAdQRUAc0R12cN1Utc93NO3gvkmE3JzSHwPaY5L064JVvXIIrRnMIdEuAqgCqgnDBlfRj8HLvj/0XP4huKWMVZozNsXDN5+84kHlfB6xvEroZAAesrzuw9nVzQDIvAnDyjhrtEtgeOtx/9wyzqsXmmIB5gNM1WtUdtgfSLhkv4c4pAL7uUOtzQeeWr4JIG7OARd3Ce6nP5S0HchzXYlV1mFUtujmhW4g04qoAHLba/wFMsgljFnD2bAW/JbBHXKey9nQu6Np2VVpnqBjEAHVAsy99VNcdQECzL/OF6oDuIMBvWeeilMNzqadfdkAt/eF9wOk7ROplD7z+vlncV+AZr334TyEsZN00e6TrUub37IIRKkZYBIQ5gFkAe2Betbj3FRVOv9yjXcqe2C2kj0+frdEuaWQ3fTA9sgfFntsgMGHPbQFgZwdsjwjNUaZWAUT1tKO/aNbt/GZoh91lxYSmd6//aKVqqExVM78nm5PbjFdm8bqKrbsov0VAu1CRGwApFxUqlQD2dzS4XzyhVCfZY3opzACE8aLq8943VO1SX8pGYqVSl5VFchCOEXXA+TOZ6oDlwOPsM9vj3RPfr1TFM/aIExVK+T1RIUWVUa8ugPTroLisQm5Lsa/Yrmt/bq+N9A+gHPWwD/zWfuGyriSqFkAOGbtmYw/ouDeiLsrfZS918BupFhOwuBtiE5hkzfgtsLqRJnGudiqmR5D6g4BQE574pXvo5qJKkfoJwwTIYZC3W+opbaM2XavW9hyV72W0uU5gXXOUVajZy8onxG+DgOVt6ys5tJnKuVRQsbbSH6GWfm4XJAdu/1ml1U03nHdMcK5sDDv559fDdsqhrnPnIFsHVI6NX4vK0PbA6pJx43e2mJ2pSrYDmn1gfYtAbxIE9pE9KCaaaKKJJvri0CN7UBCAlj0OvLAf1Wr8pKzPOXJDBe04WDns5lDpCu6+f6+rs3IIYGPfzJAJ47RJ1Ar2aPZauwcxeO76bF5VBlynIjsSh0pqO3XtyPtjZMbs/qdIvkedcpAjlHO0OZ0/nbgrIqRZR8kIO1qVnAsEECrh4hZ3MqNgUcfeGCyulsaoK++HSlRrYshGUTH7lbqdU0fVYmIUBWf10f6sT/sVzrp6pNA4b1lUJPYwu/Q7CPAbMbTmksP8HgNeJYcum1ckUohfi5RXn8vl+lzrzMrhboC2J4WGWgy0zT5U8kxcsF8xXMN4/Ruuoz5HnNOu5bimoiRZF8WiWwDtPicJokPR/20uJeSk84iz+druERZ3s4c5/awus7aoSneXZqG/M7JKxyb5UAC6WsaYPeAaKuroN70K96XM+Jz8rM8Yy9ulSOFaiAGduFi/zKIyjH97UolOy7oA7r9nhmql5TRpH9ge7Wrw1fTIHhQTTTTRRBN9ceiRPSjWXKMJHgsSNmp1a/yk7OaUTtZWjnV3ld5/k7HLvdM/vjfCAnvVhTq91+eu3TbrauU4L2/JNa7Hlf7Nvrif7tSjhlLJ6rYZtx8IzAQ14RQcCV3FVFx1L0BcGvPqZl3RzXv9ovp+4y6jPUf/3ntFODp/ufuj68fSPa6Eo4v2KLXLPHRbbPzUbtHNSi4QbrfO2uocZryziygAvm9vyiXEHXYiUrfLfsFhLlw2NeLSml5gBHP7ZKA5ENuKX2tzmESH7zgaio2afbGztPtiv6hWjIunnEjklKRP6sq+qM+FM/Ubk2i0vAN5rjkQ99/mgLC6leyC22MSDy8SrlmrH8lvZH0WS6o/jbbl3yAGO4izQI+6uUiesQ+3XvuY0Byq/cgkM69c+NiwDKRVyPyopZ9zm5/bqjTnWN2eR6Rufbzr2TkpiG2sOSJsrpf32Ms9ZsK15zfFvfpcDOtgYHuo185SpRd3Qtzv2j1gcZdF0utJcw9Lj+xBcRlm2AQPr6tglzok36hsoTIPF6XckEWZ3n2w4ad4giQeA1DPHLvcjZc5v89g4mh47pMZM3eqZnoGUHZZP2gciR1YV26og4K1iP51Uz258rn8fkGmltjIs1ELoBv29kg2s9H2czK6Gvm1bHymYhkzjhafz52/804kqdvoJmFtyw9DEqcC0vuDz1EyGprqL7Vj0KTiXrw0NgXsPOyoYDyozYzkpnII2SZAHD3E2KvawcZU2xXUJRWsTI2pVoK0o92XDdHo+NMtiIH53VJdY3OB1Wlieyybdaf1DRWUaUntafeyjXzG2B5q3xDDkRxenO1M3Xyka65YmkcvZFxRW3asqQW3RwS/oqKND0PmeMK9nTNkdaRMvZweyCuR/c6yjkPVK5OSkZqIsXp8pvXPVMrKiLnoHCIFN/vAybsc1tekQL8VpshvuFC/vRF6ZA+KiSaaaKKJvjj0yB4UgQnrrkanx/BAPFWiLhm6c9Fs/GEG7+92j+XMgGjPG3Wd1iOPvrT31D8/XZAfG3OX3OFuWl1eXV8KZR3qi5ITYzOC5gZkJO5ylDLOb+wxdkgqnL6Wpelxb9GlFCKtWRkq9dz6zQtRH+2NfEm5Zc6kAtfI982QxyRS2S5dkM/nRJ/L26VCy9pfiACB5JFW28GiTiFzUiAW1Vt/LJVTBoZcMGXGaR5Rh1IrL4VFkPltBTiIPz1LJHlXWx9nU7ODGLjbUpq0SG2/lXvbY8LeyywqInUuqC5lHm0eS++tHvOi1pkBy9fKOU5BIrSPP7UBtWI0Nklwdh9ALRHsJvFQtsRcQ9j/PMc5AohqMe/62UnqK+tTChDUgF6nVmug2UtiHy27aHiPBmYnBuhdbtnWxzmZMTvMGNWlGJdt/jSH0tdQTQV7FgMzD8vzVSiuU5AmVBc9iYKB5R2OaumzZ0t326j+s3/QtQDg6LNtUdb+S0HGdfUGnFp69MgeFBNNNNFEE31x6JE+KNZdjUtVDprB2sh0eaFWYx+SAeoqjpr8DvYeiAbE3O0xMp9dyfH0uYOCS1UOx4xN1NOjGnUakLbTmN27vnw9JM6URbdp9Si4+x0U+8U44LFnSF0BR8hves8qBxlmKAMHtU63378v3HR1xYBk9e0WBL9NwWe79NRmrI9jEH1b9Xf9s3CpVvtLHqxVcPCZW6SVWcwjJrG1XLGi2r3hNbZvjbxXXehFx7EvAXHjjWPUJvfpZLMhzO8JRhT3yvZbeTfaKmpgfZMSt88iuc1OSicKs/dUK5WEdQ6LVCvGUvbimuo3jNmJSvGXgtOV99XiThrUdk+kGZF805otJOVLLiQum9fcpvVIJDYktwEunhTum0gkLyb5tz1KwZDUSufzGIhRNkesP4kg9oIgwX7NQervMZfxUKNc91ndczIpRySc8vmzZ/piTfo1urlSsuFsD+XaxZMVqnUqe3NMmJ8wNtd7ThFvgB7pg2KiiSaaaKK3nh7pg2LV1jhRhTX1dG+ceR9FzwwDfd3FoUP1njvIjcAsxHs9F9eCc99RZLdQneYOXalrkFBdR6jwpgKwOXZJgsh17kh65b63xrBQXCHCFEWm55X6LsGFNGOCDpfPs9shoWgd5ifphXZRSo7sgL3Xd9uUdlZcvZ76NJAIKHGAcQ5d1X/c87TqUd/DhtUOYy6VfYq2m07QY/Nx4UAwbyy/lrmdS1DdksA1Y3E3RE8XIhaXYEiAnNgj5F17hknGZX7CmJ1mlVGbjms52X5I3qMAXD5BWN2sQS3QLSlKYKGSuhKVsB6xT1ZUrFEg2aKMtkc9fT+JTZJGJNHrz2+LMYxaACZUF+l59ipNZDr+dLP/vWTbsO9LO1JZfUndoHMKMq/IQlIj9XzK6tKfc0yFfZWonGdxTRDgwJifBNSnHKXE7ZFIlvN7u+15D6JH+6BoapyoLFW4o+YjxMn4aSIa9UXL+CyBVqUM6bKyIk7LSGe73qwYTJJu+NIu8fRhqW8AdW0qiyuBqjZ1kImlJpKPkbkOSlTx2AdHjGHZgRRmvX7V7lrcSS6wlK3BdgGABMF0WBkpK4+P6eaC/RQXCQHnT/rxsUSmDhgzTjuJsRl/EYMxYa/usb5csLGumYts8c2MRg8R7fP+oQ8kY6tbuVJ9tCJRdWp79l5T4Lx86qpK6PIJh3aBCKEtkOAkbTcV3EVWHRb31csnnGwsSs2+9Pv6uivWmmuk/t0cuHibQ3Mo8RmGwbU9JoG8z9qfv88+i7S3aw5FewWxOPUPkThuGI5THu1856tmqM9YD2EGr3x0V43jrZu1qc0GY0V955O0dgCgOkeEGgfkwAkVR3QG6gSq3RDzpfH6w1IOINun1NAf5465hm8BapxEZjfDetrrc41EN5fks2c82j2KuF6hRlQ70Rvgq3J6pA+KiSaaaKKJ3np64EFBRM8S0T8not8hoo8T0X+p128Q0S8Q0Sf053W9TkT0Q0T0PBH9NhH98aysD+nznyCiD2XX/wQRfUzf+SGiK2OHI207j0bZKENK7HP27BHxUozj6uOtyHv2/G71kr1XcJL5vci5Dt8dM7x6ExlNsu09tD2mq9Fje80oApO0zca9PTRqpHJYVxr8wwjDTL2f9iuxJC3K26HPOA0K29zY/bFc1WR4NfHvrpSidrUFWo+CuIfHQ2owNfF/oDZI78UiRqo9qkbTekRjf7+v+hy0/VQulGsuXIi7ReJeDTXUEEjlBSqwgFyX6moGfAsQ6xZi4LZ5wqRq3FBy/kEjkkOtGFScrnMl4+BXgso6P+mh3TozUkvLmoOyjy6fLP+u1plkSqwBeOVYtQsalfzaPZEcogRi8PckbqzUG8fF7ZFBjOt8OGfYAfPTALjkvu7XMu6czZtBALDic5Er1T8UpK31eanWAolzivVdt0CUSphNksvUViidSa7/QQvqGE6lkcVdSVpkLrRvlB5GomgB/B1m/moAHwTwYSL6agDfD+AXmfk9AH5R/waAvwjgPfrvewD8MCAHC4C/C+BPAvgGAH/XDhd95q9n733Lm2rNRBNNNNFE/7/TAw8KZn6ZmX9Tfz8D8LsAngbwbQA+oo99BMC36+/fBuDHWehXAVwjoqcA/AUAv8DMd5n5HoBfAPAteu+ImX+VmRnAj2dl7a4XCF0gbFXx2S5K1sK4Ab9O+PbRmHaFXYAWu5V4wQzLPU7DEQ8wXPpGTx7JR+Ea1WlmXGjBxRDEmN1zDdz1DUuJKTelzIj1lOck6BkGy4oCAv+BITk1TmY2goI72uE22+2AD6nO5X1DeR1wcFQGHc7vcYEmC5RwEIPyL3pcZ086K+AMOAvyytBt7T2Dboi2BCrftWvR1Tf/FAMIO9xjVY/dl2SJGG4r5fKsJ8I5xHwUcKyYYChcd8FpPA4+nyytBqeyvB00cBBY3Uz9RCwSRrXmwoZDQdJt1hdcuHF2C7MhiAG8m6kbulUvMzqbfrybJc7ebYHF62V/Bp/9wSR4X72p4TeM0LqU8jir5+Z6es7Ns/WcSSlhJtLQ6omRtTeMjEzSAkuuCcoC7tj63gLuNCGTYZ3lGgjvU8AdM0VcqnZJohXJbH7rGy7Oi1BTsVu7VueMA1aPSxm2zuYnjIsnfVwbxALrsT3GIAfLw9IbslEQ0ZcDeD+AXwPwBDO/rLdeAfCE/v40gM9lr72o1666/uLI9SuJAbSdR6NYzN1yqLoBpGOsc0w0zzfB4h3dyHcpvjjQ6DekTC6MU4V2Kw5+WbAZ/HZ50oQKCWhs7Jv5mUbA7CIMNsP5iYi6BqR3VRxFTuVhwrH6V+kE6/NyQZPmHu4WIh7HbtD2Lu6N6bDySpSJiQ5f7DA/lchYIhTgdGN1j1HpY0RA3YOmJ87GwryKjEbGaKCCZIxD2pO8X616hyGjBCrMymKmYnwtShvI1FvEEQeKqZwPZqh1rcK8K9UXmr1txXBbgXEPdYJzt4NrfYOKubK8zfBrUXNVl6m+uTfY5hqBK80aF+SBg5dTpUw1yi6NUXMoaq98aTRHNrYjh7L+aWCDfZqdStQ0KzZXvpZNNWPXDA9r1OtpFyMZsmRg6iDiul6Ut0bMD2jMm1DnsWXNyyl4xHnXn+sC3EgCGqivmQrq4ikZJ+tvv9GMfEFiKt4MPfRBQUQHAH4awH/FzLnjHFQSeHPKrzdARPQ9RPQcET23vrd58AsTTTTRRBN9wfRQBwUR1ZBD4v9k5n+ql19VtRH052t6/fMAns1ef0avXXX9mZHrA2LmH2HmDzDzB+bXFghMCa113n9WrvsND7jone6xAFhhicckB4MSHzuT7Z5RESk+xrVQZnzcEZlsyWQeapQYaOcinhJxkWgHyJhewk6JKZVF5TNm3HsAO9AclX0QNNqW2r70owa6mUJhb3dXKI+Pafcc2kWWyCk3AubvmFrE3HVH8LcA4P67+vrBrOye8T3oGHEmAfSN2RYWYe+U6qnR5sVnKdBgXLo9lW47imooa5chAZhLMgVgeTf1vxiZWdLtZmNuLtntQjjOUIvEbQi05h7rGnW7Vdocy/Ocp1YlialgJy628/uSvEjGRR65eMLHuvZdq0nflwjpTH1k0tOOcbPIbJoNxWPqgMMXQnTH7gzenzNVkc5jJonkHnOPHZSr48leJIhultS67ULGL74X1PV7ZL10nRvMC2JgeScMnt1/JUTUhtL939B/xQ344POlas/G0+JdDGUWrI4Cb4IexuuJAPxDAL/LzP9zdutnAXxIf/8QgJ/Jrn+Xej99EMCJqqh+HsCfJ6LrasT+8wB+Xu+dEtEH9VvflZU10UQTTTTRl5gehlf99wD8NQDfRES/pf++FcAPAPhzRPQJAN+sfwPARwF8CsDzAP4+gL8BAMx8F8B/D+A39N9/p9egz/wDfeeTAH7uYSofAqFRZeDspLw30AWjZwvYpYO83JXYIpU5MLqOUF/CSTkEEA2Hfjs0YOY0SKf4AMoN+sahNQfyPdeIq9yuqiecp96NfjAZj6taAbWp9DlpANc+2ZPESMo9fHELkBqdd1COxbO+Jlzt8vUU+HhlakfjpKItIasDo8AXijkc9F5OpGijjjhKbLuojxBQtKVf1eh4AMBcWMdctzcO3TKbey5JzNTJP9eU6XetLbmtgYjlGQI2113ELarP5aclbmqXMn/vvcdC6xP+EjvlpPVT+y+F2JenX+7AJA4IzYHcDxWiLSGlR837i0qMLajzSdYNhdRo85EwcDW1ul7ecpLnhVgSkVHvuRxVuf96ZmfcRW6j9ixLZjW3sdFXo9PL8N081bKkOBWJr9mjMqkQAevrFF1i+0ZoSaMsz61uSpl7r8rDy9syToa35TfiBPLkr69jZP4bpSsAB7RhzL+M3d32Z0eeZwAf3lHWjwL40ZHrzwF434PqUrwDIASHoLv/9njHcz4lfWF35fjLM/u7V3qIxrXhRhFCeeYWA8vZt/WQkA1Xd64sp3G+CQ08FHqG6n57ugVJRCqQLU75mPmwjyXPke8OmoT+C1cbh3kQ52DPXjxRYnrbM7f/2BxAi+aQset4dj1TVHUpXidGY6qneOhFL6Cx+gpzETWETGXSoZ6KLh70Ycd9a9euFUWICWYiKTQ4AHAtSXvieU0JlC/MA3yWeZG6DE4mCFwGNwLuF5tTSflclX3UHFD03BL4FNlIDBabGBFCO25cLEbwzQ1g75WA9Y0UXby5JhtcfSZzzHVyeC9vM1ronKnMCI/ip/3eHI4sqaxvY0bD2Dd6WDFAmWHcyptnDBYtW/C6N7tM9fwQe+bgHOoQ2xvjQRhFnAd7HsbMKPkqoG1dph6V9bk9IlEVZc+HGUVm4ubHtjh/p7SDGSmBWKZ+bdVLrTkk7L3GkYnaHkuCpttft3jTIdZTZPZEE0000URX0iN8UBBCSMbsXWBs2yMkrk2fGYvMjmqlOoxKDACiUW6M+w6a8zjGb2yz5wiSgKQn1kaY8YZGo3xjNXrfG1V9EMQlcWxEKXPbpKERtqDc+Dt22+2+79eJw8oN6rvyB9v1qxLItHvp+XZPfOqjq283BCLMaVeSFuu/QVxDHj9RSEZPTIlKAAAgAElEQVSZQwSnNkbK3Th5x/gEmYtEvXnhECOH7VtG1aXOi5pLbVj+DWJ0c4tITuWGCqCOcPD5UEJcNSKpdHP5lNd4Ca9GTiZg/yXG0WcDnvqVhGIogICEdo/Q7qc+avZFioByt82BSBirmyQSkkeMIrf65Wu13Zf0nLla2G/K/miXGKyB+oJjPuyimyuN9Fb1pqukLM76NcHQ83iMzxWgmKFGdHW2Ovm14GDl6tvB3HMirpEzfKr0LGmCqUHsDZKkcv9ddZRmI8CiPtNPmRwUINISVgWfIuivAq28ih7hg2KiiSaaaKIvBj2yBwVDTuUACYLbxT3WF0gcbG4H2MXEjuJAKed/RW85TfdoZCe3fYtyuPCecZ0z3Xj+9ca46R11dZa4xZ7fH6m7cpBR30zG1T7YaJcTERc69QFZkJLqfnOpLaLkxsLkx96rymXlkekon4vcknL19QUn7rdCAVmd6qo/Aw0kpAQbzgkdNS8iZD/H+qgHNU29aPuxehjtSmxPPSh5m2/stQxDOY0vpP7NIa6jXjxK0IzLx11RPfYEQUdFNHj3g8NcywgeqC6SMYGduAhXK45Jf4DkBt7sEbgSA2p9JuMEoExR7FI9I1dfQd1uk7G+nxrWILijkEGCKTWWktfSqJq7cY7CUMRPajDog/xSuFe+38jaztPLgoYYX+1e2YaYLqCHF+fXHCXLfgAtmaQGxcfKxmljyZ5cZsPRz83vc0S3NQeWbvbmo7KBR/mgYIgB0uIlVsNnHGkEqnaQTeq+aiCPmRgYvvLnVGwcUy1ECHKlIt91vtlnG+jyrm14aZEURDt+ZkXFS9zLER3FfdkYrlLRUG8T2pUDwzal/sZm1M3LDZmzjWEsUtUy+PWzE6YPovCI6WayKIJ5boTxco3aRdpd8hozC2hcu5/FLlh9dxzMXJVQEaMH7K6od1XTjEbF60FArYxTPj+6hc63JnkfxU9lUcn1mRyiLjOg5mCJ+QYhIHQUfe2JBTCOsg314m0OZ1/mcO+rDgbVXd9w6gGlbeqEEeFKVBztguDalPfCdYiZ6FgZlAKmfEODvuxm5bXqsmw7kZTrRtTEdm7bJh3WPtPJyAPMQH0qD/adJWIhGtktFU/9GiqJGVk/RhGePa4LeyH0DshYDkkcRe9TQA9qXS/WF4mJClWpPgs14Dfpnh3+do+dRKkDMv6zM1X9PSRj2KdH9qCYaKKJJproi0OP9EHBmUSxS6xf30j+yf3YhjEaSyBT3KcdWFA9ldWAe7TEPdEoCmzUfY26YVRufLbH3UY1GITLzW8byKCVDySOJVavzy1HbukB3DKG3Fr/ZuTIjbSt1WUZv2F18RoVOzB2G7mSC6rWIlbnz+dw2n2JLKkqRsoOGEoAxlVTUoXEcu1PM+b3hT/l6K5qy9i9fpKe0QbYnMzGMiXJgUhGuWGfE0dLLTA7y12TU1kWg3HxthJXql0IV3rw4laqQOJiyToedZboSCRWdbPdKmT5jFIu6AyzyaS/BKkt80I48jRIg0yUPSmPiLG+lqld9Z4jFiN+MNUTF9JxhOaGSjruaok0lp8RO+X0DfNJ54I4JOiYaIKoEhPftAZleW4rj61uEZrD8l5zQGW7s7aEGmiXOg+1j80d1jUSyW2q6HYP2B6iUDe+UXqkD4qJJppoooneenqEDwqSoLsdCJNm48wTdUTskyvQIXnvioC7LKiugDYmhRnPrtWXPZbTZRyWcq0xYMewcCiTGEjhlgkxreODKFSi55aUpipprUQn3Td0yvfGlPG48lvsRmwU+r1+hC1pO2ZnPOpxuH7MOJ7MRpR/i0q7y+JOECNeblzcZd9Axj3lRmmL2HUpiU9f+pJ3szlCWZuvQN+9cohyCSaLLjbiEbyvCDO+6OKckRuAy6HnO+mrdk/nJRn8N4GYcflEEmXCDIDj6IJa5AI3zrwVrvTO1yQR3G3ku3uvciG5xsRgQSKC6wsu7DFuy+JyjnQtl0iiHSqj67/fFMGl9VnZV1JfSlHOveV89JkQpV63bGPfHb3QSrAaiaYBhOEO+IB15jqRrmZnmeljVs5v9uJcMwwiZPiq11g1TY2tz+ABi0TtB+PNThjVWiQOG0Obz+fPyBqxIGRqZdyuWisPokf2oLD+tMjs+X2ZhQ6l0XF7RGgXsik2I/kAjJJn07ihmwjgDAphjMiez9RKsb4jmfNizt4dFBOujzzD+l+h6cnyBFgVDXhwl2puGHrau1bojKROo27mpOB+lMRre7PahFGVXrdI5RdRzpQ2m3zMLp902hbdaJ353I+PR4zr2EH1ZflucdBRGueYSxy4UjXZh/rO4UEAMS4OoGWod4jm9WkotjNX9xWGUhKVI2XqJjAilIjbltDndiB0CvfitwLgZxsRscKht5B4CS3PtVJWfRESg6PjxF42c7sX6gSt0i0ptsmcFnIVcLfUiP7M8+/+u0VXHKHIexnxiFg83mI+iuxeAE7f7vQ5iKei3r//rkqedRz7YQC5soPxtH4IXubt8vWQ2qFrlEPZLwn1YHjQGUUYfZs72XP7r4S4bzT75XvtnmaNJOBt/+IE4JSbRTzJEiKF38rB77qHU7+P0SN7UEw00UQTTfTFoUf7oGCC5ukaZLiLj3hEf/n5Pbl2FagbB1KVyYgqIPP17pOvS5Gy62fc6zJuQ6m6VGNUDrGcu+oayN6O6ro+PHfOrGpd65WIQd7UBVcz2UI73F9zlcJYHwyy+pm7nqdxiUo5qNE80/q9Qk0RhHsO5j6ZcVGDV4nF2GfSyQhXl2NGAeqCOBrZLnmXKf4c1tPakzIMDp/Z3KD88aT6cFyotKxvDQgQlj0tr2cWR9EciKohYkmZROfVbTZzj40qDP2eSQDGtVvMDYVSOmr3RGI9e9ZHt2YAqC5YocmB++/22BxTEf3bzRKn3VeRxLahdP08/nRbSqa9aGIiTR/gh3pA45xj8VlGwmufshSXiO7ABRAfMJACy3uKg9UKfllMhNQR/IZSfJLmsh5ba6Fz5Tol+ecaHuSzvnzcRYyxal3ckgRUur7ufu1RlOwAYHZfBdFGNCz1OYszAu1w230IerQPiokmmmiiid5yerQPil4AymiyoTXQqL7UdHZE4wZiIoDOx8FQmBFxWuTvvt4047Izzju9gHjPvru8K6lArS59GPOUIGbYXsLQADo7HXLNm6OUuOWBdEUgYv85HtHldnN+uO+ovr0+l/oefDYVkle/bwtxjQQpDnCBRtwQgeSaSVZfLm0hA31tLg0oR0jE2te9Ctq9XBfNKMfZLqrzhO+nQjX3Z7fD9mESrCXfySQjs5eBgeufaHUepWsGob7tpb7sZgCCSBGsdTCDdLSZOAkAG9i1gujK5/cQ+9lycG+PBc7cXJ4N8to1ANpUf0CiuAvKusQR4/67yzVYDK/2gd9AcZy4wC7zW8bytRD7ii8NIoFx++uqOB4WBFokTMo/SuPzP9TinOG6xMGzZ8n7bvMsjKx/ez/QYI2S2oz6OExhhihx+Z5Esb5B8d7FU6ZVkb+310TqySV6C6582FTIfXq0D4qJJppooonecnq0D4os4K5POVduCTwKKANVDva5+Nz7oiwPkbWJWELZ/aCh+ZGpy3uWR36nFCBHHWVlZzaMi6FdofhmXbZVoA+4+I5xEM0hJdypXZLCFaiZsZ+68u/yoVKisWfbBZWcjD5j+Fxn7xiHRqFQosOGWjBuDl/sUtv61eDxzurbKNjxsE7GcREKHTmR4BsJGuq47jq2PUtsRFYfEhvEAKnU5khLAhGS1z+XjDyLFKaX3JZAPo3H6oYv+8GmAQuXmtsEZmdSltnt/IZx9JkuIbaq5NXuATd+dxPLkz5DfMekpM11CcQjzWFBnfxc3RKPJKdpTSNWGFAEHs5OCOZ+HG0SKg2ZK+vsTMYm5/DbpY1NKSWGKtmtiBiYZTAfER2YY9rX2f3dcz7vT6mYzo8ALLK0szFwL5M267PxNeZ9CTviGnn34POh9O4iLrygmv3SjpNrG8wmY7dnJ0B7gGSHOpS6Pwjy5ip6mFSoP0pErxHRv82u/WSW7e4zRPRbev3LiWiV3fvfs3f+BBF9jIieJ6If0rSnIKIbRPQLRPQJ/Xn9zTSE/fiAb4+A7aGKZupqmSB+Rwysi92hiyE4AdnK1EQ2eUNHRXkxCxsgg+0Ro1yNTr5cZE2KcRRlfUYhkJFtRL2NLoxguVjb4wTJsqOVhWa/Ox4/CBgJ52eE+kZpE+vbBY1mF4wYNVck++knQmr2CZdqhGZXbgp9I7NfU3l4ZYc0BcL8bm5VvOKcJI5GRYmiH1exhYrHo9b1m1LP3oFIkENg5NtOsXxQl1HvXHFy2w6EbiZG6hxfzG2yeZUbdy0r2wyAk/E8e8ZnoJGiVmkOCOubPUsvyXeaI4rttzgXv5XNO8zS5ieVRYyjsAPCHD2IgO21YUS//Z2S+5T3BUeMBNpf6xzb3ZbuwH7eqUusZsHUA44rUxn1mkjpmbzdsW4k9T9/m8PytrjSDBwYSBgzjDBHviqzexlg5uoxKsvQdwxjjIIyt0rVZWp2dY50sEBBFk3bp9ddAxDzwCj+sPQw58uPAfiW/AIz/xVm/npm/noAPw3gn2a3P2n3mPl7s+s/DOCvA3iP/rMyvx/ALzLzewD8ov490UQTTTTRHxJ64EHBzP8SwN2xeyoVfAeAn7iqDCJ6CsARM/+qpkr9cQDfrre/DcBH9PePZNevrpce0aZ6ojDOyc3vJZyhwxdMxbGjTDXmPUxO7JwccUpNCYjo2Qvm4hFIZHOHy3FictTsbt63evX+3GUwB5IqS9u0vN1TSY31wQPazW4H163Xqgsa1oF42A677VXdsMPAFl01TQKZpYQ7xtWPwsubGrEf7UzpPSbG+lapQyTOuMOCg83+3pFelQiFClGuMVKk/FACHCsnvgckN+WeBJO7x4aZGHabA0RUXSJBC2bHqFY9bZxxnQtBkOVK1IJcGUdLoDaLFC4qJv1tTgggSywlGEv1OWI6XOvHHIvLaKD+YFkDJun30WLtmawa8t1MdWzULqiQWHJ319lJWmeR486SAaUP9OYNl7dcI66pbTavi8A94p1pg0PP9VzqJH0X3eEBnfzp7/48bw51XFkjsNVAH8depShA9pnNjZS29s3QF2qj+DMAXmXmT2TX3kFE/y8R/T9E9Gf02tMAXsyeeVGvAcATzPyy/v4KgCd2fYyIvoeIniOi57b3v4B49IkmmmiiiR6avtCD4jtRShMvA3g7M78fwN8G8I+I6OhhC1NpYydby8w/wswfYOYPzI6FVTGJoh/mb9TuJ/3/2bOuCKbLuQinnB/n6RUp3QNwZT4KX3VFeWfPlFChpuNOjVHdK7AzH0V0l8vcbnM7Rt8mYElQYjIdSuirBqlwpTHbvrVLzc6q795xvzlIunbK6r3MDH9535suubocHztizWXBiFy5azSAz3TN0fA51FenRFX6jMvsGIQSMsGEgdwZIHN0CLVKmj0E2FF7ww5KqUpHbGNm+8juhWVQ9tkNdOYhM/6KQVkTCmlfWGKfUGUJrUwyYkUtzTjOVDZj73bA7IRx8WTaHsw9s11KmlN7dvkqgwIluwQj6sQB0Z+zOnq4VsZCsJuyeRwdJKQ/XVPej6lX7Xk1kufJwhyJ3aabIzo7AJB0qboWthmsztFnunIN9mwDA81CZuuan4p0ss0QbAvbXc/+lbvNh67EhGsOCdQSzp8ZcvvtPqKdKRrHMycdK8ZclM0G5Fdyrz6TvzfXCfWpQKi8ZcbsXUREFYD/CMBP2jVm3jDzHf39XwP4JID3Avg8gGey15/RawDwqqqmTEX12sN8n4Giw83nu29kZo8hnkssoHyHGaBLmViG2VSA/xm081hxKgbbdwdGshwqeqBC6qkrlFy2kY19M08UBJS4OpbD2BZ4XBAjUNcl/tAOvZzWvY9HU9yuyslsz7ULSgcYkvdGcyjP7orMZkqbCyAqj2rFmfcKrvTCyg20Vv9YLwYe+3hTOiZ0SFnxsmaaMRRAOmwKFZv8cFuU8RCZ2kNwqYb15B2G7HgPkJzqCm9OJOqSHJPMoMr9NtuA9HCYnTKIU/st1qa65Igl1uynNlBHWN1w2NwgbDPY60a9aNglLyTAkuSouiN3StD+CjMAFl2s3le2YZuRtpuX/dkclLD7x8+HtA4y1dHYmB+9EHD2tI/P8trHAzI39m+OnRz6AxWirftB0dKeCri85cCeolei2b7jXGJR81yVX95I8oEzDj7PYmzPquS2ALrUJ0wc12e7l+Ya6Z4y1+RHfiN7XqcYd91cVZPVSCT6Q9IXIlF8M4DfY+aoUiKiW0Tk9fd3QozWn1LV0ikRfVDtGt8F4Gf0tZ8F8CH9/UPZ9Ykmmmiiif4Q0MO4x/4EgH8F4CuI6EUi+m699VcxNGL/+wB+W91l/y8A38vMZgj/GwD+AYDnIZLGz+n1HwDw54joE5DD5wcetvKEZNTbHgmuiV2P9ylx0XkkrnByXJRFBPD+FTDjndsZrTxIcZiJ00DObacPRnVZm9RjOUXo5xG1it0v1BW9dIwgYH4SRLLYjBYxTiPcFOn3dibmQVbP+Le8GCoM3P4AVU8QsL2+O1xUDLfye7skdHOCXye//CJZU68Oru/p3KvexRMZC2xMNw2fiy6GuZSZP6PjYEbEFH9RltMtjOsctjOPz3BahrlDssUCZAmAohq0VSmhF1OyuCvPd4sM34cQU5S2e2LErs8ZR59rxUDNMk9dx5JsKhuW2Sli4ptGVUFEpeTi18Kx7r8a4NciXbstgDrVFSjjmdyWVGWWrokaJzXm/GnBR0pIzpokasSYvTkmXH++ic+RpQ2gMuGVrb0Q1b69ARlbKCxzqlrJWMeUvARU57kkqf0PlGuXgaqHCTc7ledXt1Jktn358MUQd2i/LjUPEV6c0viaEb/dE0nc1vzB51RVl2ORvUHa5cGe6sP8nTuu/2cj134a4i479vxzAN43cv0OgD/7oHpMNNFEE030paFHOzI7o777WK7LjIFKOTc8xtUxQLOw8xmTXvqcv1Nur8ARmhWPJI4x029busi8uLzsaA/YYSDtu8cWf5ukpQF3fpvsJ2MBd2P6XsM5in+zGqBzt82Mck4RQApS6+fd0N+PPx3yqo5SN0vc3tELnXCqWVRqu9z9suWjiE9kdhJQcnQoHsrui81J34mpbMvvFWi/JO6qeTlxTjCGTgBmryJ9vt+flwa3yumZ+F0twmlOA5d0+0QsdoCQJAijZp+ilMf6zvmTlXDYJGPGTgyfedIoC1ad3+eYVwIQXCErd+/VAK6As2dcDIRs9xCjyDfXVSLK1mGYcXRIANSpJEbHax/25g8Roz5jhMYN5ig74PbX1fFdXwV5xnFym3Uc94vqciiV9O0hfVdm12SSFSBG8UXmUOEZ65s0Ol4RXVavba4huhOzz9YcMc6fdnHfyBEKQIzl66lssztY/hDqpN/ZSX9ePkViJtvscCd/CHrkD4owtuNnVK3Tpj07lZ9iRCs3ffN6QhjPX/2g+Arxekqbset658yI6iUunDqpzPJvHLwUegukFL8HMOOU1TMajqlQc/GOqOvi8NjRTFPXcTXc1ADAb8r62IZggHF9On27iwbNXZT781887iUhi0GXhHLTKRwPAHQzjhtnjGXIF3++AdkBbuqdrA8p69cUD1O2n2i41wsYoXWGfh9Wn6S+yo2UOYVZNla9A8ogY7jimHCpzRNzMQDNtGbw5gBSMixI+0Ml42PqQZ5JzuvNNSoPfk5tXtxJMBSUwUKsbjp0OjamRqnWiMZha0p9kfo15n3OVG/L10qATHYoYm2cjWUPZly80yh5USGb15RgPwDArxjcU0e5fJ649P2cgof2japzSKDnbZOXh6jMZpi/H6jYS6KfhQPmd7lYh66X1S5Xl0fPMyCOvzn01OdJDQikg2h7nIAD3yg98gfFRBNNNNFEby39kTko+qoeo3Yp4pYDizsmSlVEn3izu0ucD4NUq/FeTz1U5Ql3VIIhYuVUhYskBuA0GQ6GKi0z4o2ryWic87dnLTJ2Idcid/gAEMVRI15Un1AZD8JUPN8c9N7VPmlHonOhxl9x63ODPjWpKHfn8xt5p1N3W3YjonTGqQ+T0ljZ+jOP5mflgvNc1KZqcCHB2EcHgpE25eqlPjhhIHCdxetkfUeBCrfaqDadG6qbKzhu+5R9h71w9jmOj7nMJpdg+aVaq0pmK23plmIo7ZZaz5bQLYVLrS7TXPdZmtWzt7tYZn0qRbdL6W+/MZdZrfo+wAoz7hpp2/JOkgSqlUqbWfvXjxGiJwp0HHvLcnOD4LIkUrGeK8bRp0WkcMToVuIeSy6DTWdVO5ra7wrqrzNi6evlnXzuULlO2eKNRqRES+LUmx/VJRJSgD07Q5wX/TU0O8v+0HbYHrh6nNDNgcXr6lDQiCTk2mECpIelPzIHxUQTTTTRRG8NPdIHxSA4DaXNARDOxoLfci6fexxs1P1rkph+OcOPp+87sEbKJg5skBRnRA+/fFX0szmXntsgxiQGM7ACWarMMTIBQfulz11fHZ09vORMAsrKHlCf61Xuu1vwICkLkBiu5jDZaHbVg5Sb95tMz0ojTNtYEqMRoyIgkkkRnZ9JJ0UQJDJBpWfLyj9PQcYyx3iKRuc6CMonMhuFShXss6jxXRxuxjmHAj02a3c2xyzpDXvg6LPpRleTSBKKU1Sfiwt1fZ76iUlRl7NI5vpMbAVhRmLMzrDEYorTyyQlWvBdN0e0rxjHe/5Ubs0uo5oJ4n6a4zS5FtG+lCcusn7M5/L2mHDyrqx8pjgOYp+RQTMUg0E3Zzas6MgQ7ViyJusLxvoaFUZ9sVEkSaGMzE5t8b10ymYbCjMIVHs+VxXS3D6do8duD4Ew75Wha3x2Is9fakKjbiH16xYlsu4boUf6oABxhPDIN2ZnngNAikWAgmfFd3uDooZHPmgHm6jFZ4TOZYu8rErX+mLTKaJUCRH6gTLjmhmYSY3Seb0BDGMW+pu7SxsSgBRfACQvnSvOg1HShTTq629RxGObGSFNaqSYAwDwKyryL1tMgCx2oFvuSgdWfqjZoxJsjaWfB4Bu9l01rvehvXmsT7LNzcrIo/zJosetTq7MrOZcQKh2aO50s2kPMNjY7Nujnm1mbJ+FQrVBLGpQ6wPXCkNQn6cy9l5hIBDqC8bZM2mZ1xfStvk9BoLOGf1p7apWUua1T6aTszlUz5ltZgAm+RskB3h9oSqri5TNb3EHoFmXvo0ygtx1QxVQnleFVMWY33fE6GYC+9/vy/k9ZUqUSfEaR0GkUf26XmLmv7Gplx/whZMHxf2EvUa9EwOOU5ySjvX6Jg3nAmk+ioz8FlF1aOphe217pM4KhJg/xNbn/AQgfd72PjuwBTBRmAAHjmCD9emXJjJ7ookmmmiifwfoj8xB4bY71ClZC+f39ZIZl136GwDIib/1ThhyK7KnEiFiOF+6x/YjIM0fOld5VZeiTonusdn7ADAzsLZcxZZLQT2gwdzt0DhUU01EPJrcMJeruYBMx7JbDGGffaNHbocjwOELpZtvGZk9/FZuWK/W6ZnmIBlMTU0TxtxjM4ljrOwrIaXtnkttdC7EZEFRtaTzxGVqJhAX0pFzmRtpRwh+BGguc/0sJBji1J80TIjEueqHlPMMiaP1jfwMdZlvOcZRqLpne0yYnYXEYbOomfZfCjF3tbmoMklEdx45HWqKhu/tIUlCnSyJW6gQXU0NfNBiX4gYzb5Gb2d9E+pyuphKsHANb5Dyhmf91hymduTSG1EGd0+sYJlXu2YPHDx0abR74jp89mWploX077S/8jHbsadYVsBmT+IgmElVnDpu+p4BP1pdtkcptqLOVOririvOCY26S/uVfKdb4E3v+H9kDoqJJppoooneGnpkDwqGGKkCExyxpAEdIeoEZZWIBQETSG6qGVl0dYRERuJSAFUju93sR6URoPG7IeNoLADHOEjjChSmeFeeboskTYWWf/YD3EJNw2cUsTMyRX37Q86FWzW6xPGVbSIx8lL/3cxmk7+jXP/q5sg0s74AhoGDGTVZEJnpgfdeS/r5AiLbijbOdJb+Ltwo7V/+KlvUuf6ZBVw5bYcFVxFxr4+07FD2f55WkxqC3xIcqSt1LvUQBvYYAAiLnjiYjSGr80SYWZIikQ4i9tk+AVVAN6NoEyCzw7Cm6lTbwsk7qhTYSIJCvLnuioC7UAnX7BrhUK3t7b7Up74EXMf6PlKCpCXimtp7VXxsc1sKe47jxLqWq1WpHei7vjti+Ya6lefzeXsoUeUmUVuAG1QqimPTWVvL+dOXsgsJ0HFEygWnfpB2ZIUEEmmgn8QKJSYcc0rE5bc9Bxg2RwAMidVRxLyn91HMH3Gq0PGigOaI0e6JFEV9/LOHpEf2oJhoookmmuiLQ39kDopQlxJAygvBkfNu9zIuoYcVHyWHs+SuVHjKQFzbTH/c59yp992Bl0+fYcw5EjbOtbRRmKth4Yqb61xnGbdDjPWN0t0z9+7oc2Wj9hzq/ew9z453u6M65YD7gWYQjKax77QLldRyr6+Cgytf6xZAV2sgonL32yPSFLbDOvcRgvvkt5mXGSFhCjGlREIAvAsJ+qTSd3r5EMwTzp7r23Ai1Eb2bDIcqbSWSz2AYDwBwNYV86BoUlBspguK6LQAUKsk6VqWtLxKiztJGkMAlq8HNAfyM16HeM48/hui/GamYiwKrCYvf69uEbbHiuzbis3QkXgDsWIy3XnfQqSQJcW2RGmSU90tT4lRjmtEJP2/fJXhXCjdySESk9XPERDOatUGlBJkCiAsuf58DHa6xrNoAwy2I8bkRcOM/jomlQDZNxR2IxDafeD4k5zyjNgzbVq/0WVb52pMPHWPAZeCU7uF/E6MZFfrxJ222d+9Hq6iR/qgEJdW6bz5nXLA4yAz0O7L3/Vp9kqM7yIAACAASURBVIypDvRvUzXxohvdRAkixhabebZ5t62XCWkWr5wchhnuSI3PId3rb5SHnys32L443M+MV4iu+jkzZF5ltBvQrixtJPEqxWGxY2PP27G66cokLnpwWp26vd0L0sokko22wHZqSfzP+5uyqjD6kdhw5cFQti1hJtn9/KCgQKhcABxHA7bNPVMDxTgKiFrBx4yIAM8DmgOGdwGeWBwpGNHFmf1IH9jGVZWDx07A7gBEd9QwLw37m2NS99gEDAnI79HI6sQV1XUZeCDJPPJr4OQ9e+Xmp0mG8oxztuHO7jP8SiKe/QYx6t1tMZhPrk1/V5dUbOBOx8Flqr/zZ+SZfOM2o3V/rfqNZNWzfNq07OIY5GSb6yjt0oSaA0EnBn+LDSJWF+X8fbY6lGVWVbmmmwMpINSMk3dlfRFIHDmSP0NSl+ueZs4nl29Lz0j9xDU3VMnZQpwa6N9dUMCJJppoooneWnqYxEU/SkSvEdG/za79t0T0eSL6Lf33rdm9/4aIniei3yeiv5Bd/xa99jwRfX92/R1E9Gt6/SeJaAdq01jd0u+b66WomEc+Gue6vZZxEJyM00mdxCCVKExacWA4LWA0UEvfZ5U2jGKAjH4rwYyn65vrJG6BJlHAVFty/+xpH7Gh5N0k+djfCcbaOMKU1AdIWE+Ru+jTGPbTLo4qUORaB+o3hqRtpCRRmeG82esZ9Yy7ulSpsNrRsdCELfYuA4s7KeqVqwxy3IrN6uQ2ievsq+4Ai8w2Lo0k0tU0ITmOEISLdPoR5wLQODgX4DOVBgXg+Pe82Kdp2N+D9J32LlN0Dy2k4VZUbFT38eQz6ZJFmgAD+y+lsplEoljdJASfOqXRaGuL5l1fp/QzqjuA63/QYJvloZ/fF6lncZclilvr4Vqpw/omod0TTlu4ZOtjwGnAnaUizd11jTOmTKLae7VU3e29XM41cwHl4AZjOzvR1K/aj9VcAmidCzFY0xFjpbhKA6j+TOotVIvZM1xp1LpdDJTltwfgeRTfzMZ2kJ+bCX4tUgAzyXTSMmxtROwufac+JVm6+i4CxdTI7Fl+1++JI4IYtMcQEh6GHkai+DEA3zJy/QeZ+ev130cBgIi+GpL57mv0nf+NiLymR/1fAfxFAF8N4Dv1WQD4H7SsdwO4B+C7+x+aaKKJJproS0cPPCiY+V8CuPug55S+DcA/ZuYNM38akvb0G/Tf88z8KWbeAvjHAL5N82d/EyRtKgB8BMC3P2zlC2OznpSuzz26hI2fAncw4GKjTnsXN509N2bDqGdt4m6YRFqI3Al6+nu5Ft0CZ0kfm3OhuRuhPFi22fXcY6uM++7rkKP7Y18vG+0e2XthmMzFgszG9LoxMG1LPWO2PNvujdhIGFjcVatfwLBPtY+6eWY26ARFs90n5fJJHALG6oo03oO26H/RbhLtOcolulQnR4zadyKZEgNBXFxp0SVXR8fwJFzc/fe10UZBxCAfhINsRWJxxKirTq7lXKJ1S5bUhrqsP6nse0MhDTOO9oP1raQTbw8g7rHzMukNdQCx4TVJsfVZieNFrGli8zkbAApUQOKk5EnCqbpWbAcGSUFATHcLpEA69un9UGvQW2aTOHvW8LLkb8vbYsjNTudMnBeUgmC3x7b28gHv4WhRgtwYTQ3K4xKhvCv7id9mkpHjchwJmJ+U2o0cB6qwXbDsRe2+2CnyPSBUHPHTONrqoMb0JLm3y6RBkPfEdT7CdVgKYx7uew9LX4iN4m8S0W+rauq6XnsawOeyZ17Ua7uuPwbgPjO3vesPJm1viAupHNgYIe1lAAwfxhEXRsbcS4o7AjcJFJCyJD8M9XoaCfd1xPA+pEEmjnlsk4cLBpPVBp99EhPz8tt9EmwoU4v1Rss8RvI82f3YByYxgi1v9zfT8d/zvnVqLCso9/fvvVcYrIGUHKpJZcb3SOM+ANSnvXzjWbl+kz7TLmXT2ypcPHtOCzJbeEY57Hm+8cSy1+lb5EQ0ZyeHAWWH5cx1gGfMfJcWJEvsDAD4WUDlA7r9ACy7OHdmVQdyktTKbRzCQgzZgGL+WGwNMdAlUMnYlHmHGHrtIBtM2eVgTU7UzSXrm/UfK3MyO5FNwt7rNAbA4jf8mnHrN88F60mv1Wfic+8yTKbV46QqDSrUKrYZVWtgeVuMpuyTAb1bANyKisiy3uV4Q8SSYCrNOcbsdJwJzMeyvpA157PD00E8kOozxLFuG8Fgcy4UPIypZKOzB3GxdvppAxiIqkLDxiJWplOj62OdO1H5FSgHWnZgSswDJI6DnXqJNYIWETNpdhTnRZglFTU5MfhTR0DQ54CY0Y5d8vCsKCBUKblSvy8flt7sQfHDAN4F4OsBvAzgf3qT5bwhIqLvIaLniOi55uTywS9MNNFEE030BdObOiiY+VVm7pg5APj7ENUSAHwewLPZo8/otV3X7wC4RkRV7/qu7/4IM3+AmT9QH0vIbhTTcmRhi9bmHtpoHm27dgXXYEbk6k495LBRSis++z0azYOTqFv9uw8znvtAR3WPcachfSNJO+KPzpQMexxQuOe2PZ/oIhVmlFbk5ypLijIaQxFvYqBeitHJyk1FUd6kJCWel2qsKOz1UpYaWT7sfj7g4pl5Vq1Gyom5hTsqXD/76kOLiyilp8Th9cmvaAAvDqQ4ioo6+NNK/l5V2G4qzKoWzgW0nQMqhp93aENaVt3GIwQH3NwA84Dad1hULZp1pRH7JOqFrC9jbIDGbDAjSR/W1ojlRXHcm4PexGVgcwOZoVWjuCvG+qY00G+A199/UERmXz5JaPcpYiNZrAAcsL6ZUgqDMhfRNhvvThMhQXM3K2aVSRKrx7N6WjR7xu7nLs8x1gBp7CQPtPRBXxVMrNICaz+eyUc99dKeqtvuQFrR/3LJLl63mJVLSblaXWRqoVyaZsVf6rUraj049St1ACrRdrTL0tDd7jFoS0krEWQucOcQZqp2rEQShk/ts5/iwBIEd6o2qeKLqHoioqeyP/9DAOYR9bMA/ioRzYnoHQDeA+DXAfwGgPeoh9MMYvD+WWZmAP8cwH+i738IwM+8mTpNNNFEE0301tDDuMf+BIB/BeAriOhFIvpuAP8jEX2MiH4bwH8A4PsAgJk/DuCfAPgdAP8MwIdV8mgB/E0APw/gdwH8E30WAP5rAH+biJ6H2Cz+4cNWnojRqoucnZRm8PLm0uo4In+GKtk0Io5O7AgxPLZHXXSb5a4MsJOAu2HkmgOjbUts/C5PYt4zrMVfW7nntk44JwqF5DKI/va9aNFqLLeBGW+g7ddHL6+INM2Jh98tbpuk0i9KbSHxz4xzX9zhMQY+psbs9kP5TlZmHuE+v8+KVJqutfsYdfHN3XBjxK1KRnZve5Q4cw6EbiG2Avg0Z4gYe9UWbuNQuYDwxAaLqsXy5iUOD1Yyn4hR+QC3aFHXHWZVi2rWSYCecqbzZYN6bxvrtzzcyPhVGs0+kG4z6bdK6LuigzabGERH3SgWU+Z+Sx2AQNh/iYsEO26LxPFCOP52oVKJSonVGnCbEX02I7nGWnlqXVy+Lu6nlnKTOqlrdQnJpwFBIojXtG3VpaaBpYTGyx4Frlounds6md8rJeQo2asGwXCg3LVtvB+lH5J5syvXRY6UUBBxzBvBTiSj5F6dSa6Ewg2VbNwCofIduKNo3O7mijvnpEw2RABDFDanhTmD5wHOyZxhEpsGPEfJ2WyxZpdlL04WPGORnjx24so9iB5o2mDm7xy5vHMzZ+a/B+DvjVz/KICPjlz/FJLq6uGJyiQgKWw/RBWQ006yKGyuU9wE6hCjJB0YlevEiDTLYityLxMmOE4wG3n2MkdBDWtpow91PnEyMLlsMtki46wcl83auECo3EQGXWHfNBA8IBoHTaWw/2qCaGAmECWDvn1DJi+i6D0ghxJmvH+QBSpt1vrHxduoBGE0w+FDRIvnaqmNgijGfot+5b26mmF0Q6KxIY2izttFYujd2MZqQH3mFZI5MhzWG1AADqsNrl27wKJqsJg1CMGBOWCxaPDY3gU2rcferMHMd+B9ws3lBTa3RD3VBYfAhMCEa4sVLrY1Vm4BDhQP59zgTsTiWDEHnGcEl1QWfZ2IbUrxoCAWjzliXD5JmJ1kXaNJbDqNvWCn/vsulV1diLHYdYCdMa4Vpos6YPW41heay9mp8ZoQAelsXgUPuFoOtXYP6OfNCTOB8aCM0ZvfZXT5QakG5xyuo9kXxs27kKmpZMM1RxJHDK9r3LvErDjHEeI+9DZO8+4b9XpSVXaohRG0w9agwiPz5Diqv5DPL9Z6VGLM9j7EORwMZcGrwbsOoiqqEgIAvGTS5NbJ7x4SPzFj0NoBTvap3LOpogCeBaAO4K0bRPk/LE2R2RNNNNFEE11Jb9JZ6g8BsRioai8cA88CKmVRjbPvVKRnc2t1itsDAC0lozcEx4e3TgxWZmzKVD2OGFUVBsB9dm9et/KM6krqc2CLjGM3yjhxSx7Dc6l35ULhDy1cIZAbZKP7LDGqMwfcQvzbNZn3qkpYhstz/pSHZYLN1Rq5Csm47uQnP1QlZbY49C+4NaHbT8+y48SJFGWl9hMhpRnNi1VGe/8lxulXJimguii/H42wVsesf6O/fq8tVh/flFKO2xDapeA50aWHV2Pp0jfo9gKemJ/ivY/N0AaHa4+tsO+3qFyHk2aJigKOZmvsV1vc2+zhyf1TXLYzfNVjryCwiyrLuevQssPieoO7Lx8L59giuVeaJkOjtU11BYfkrs0pjoIrgdh3nXD90T+ilver1YgjQYbdyA4RktqIvRjGKc8hbrDhc0kAtlHXlPoM2NxSV26N56hWjMar2rZJ452A+JLU1B4EzO/4Qnq/fJKwMKmTOKpxY0In4ig92dgmd/jk1BEREypxEhEjuUrfmlApl2odAQEyn6M6qy8JB4kVcRsBL0yqHoLvz8tsojrHcHUQad6L6jAEJ9w/JZWQdwznA7rTGcIsoRaEGYM2HjgA3KxDmFXiLrt14FqksrDQvtEywUDtOqCSb4eaQbNJophoookmmugtoEdWomAId7BqaizrRnR2IFTEMZkRACDHyZlJUFzlAqhxmFXCMnkKYsyeBdDdmTxDQfTHMF2n2DQqCinIT8k4HZ9LG7tsRpmOPE8MY+VULiVAunySSkObC3AUMo5di9K/l68xzo3jUm6oOrfP7oJH70kY/ermzw9ulhfCPLelIH7LRXjtsrxuJpybX5Xw6PFzxDh7u5WnCW0Y0UUXQIY9NaxjtyyTSUX3RLU/rR8jMQ46Rth6tNc60MZJ3xUBdy1QB3zl8iV85fIlicJmwsI18GCchQUO3RoXYYaFa3CpWbQcAha9Qb4Mc9TUoWGP51bvgdtvEeoQAz3JyxwAAD/vQAR0aseI0l8uIRBADdDti73AOL8orXWlZFVdAHCSaKg5EjdWi6o2LnR7LAiwEa+M0v3ZCWNtOEnEmN9nnLPYNbgiNGqHME796IWA869xwNJsFz2bQEsacJfKpIAikE7qXEr3cKLj7yMxhDrBbRMxmosa1bV1dDu36xH3qemvZcSyEko0ip9M0r/JTRjR7iadT0XwqSPBmgJXYlRfezS+QlV3YmgOSaIIHYHZwx00COc1oFoMrhnu0sF7Rrv2hdTAFSMctqIRAYA6SaYVdfCLFlXVYVN5VLM3Bx/76B4UTOiCQ+Ua2VxnQRY0gLZz0kHE8DNT63RwdYe286Kaui5ycGBRNc19i6ru0N7YCmQDCOG8jgfD/8fem8fclqVnfb93rbWHM33j/e5Q99bQVV09VA9uesAOo63GprGNbQhxhBRsBhkchwgBCTYEBMIRcZQof0AUEgcImAQPCRG2iQfajo1RhG3auGfTLnd3Vd+x7vhNZ9jDWit/vGvvs8+9t6qrjREu6XulqnO/ffZ09rDWOzzv83gv5Bk9pcPQjMTUR7F+uIoHkWb4UsT1QNkNyIp6ir0Oc25a2kFDSNfR3D2AvrH9IAI6ELrBQ2zr9YDZoSU6NMtaL/gxaRhYQ74fU6TufmNH7wEPoa1Eq7GPQ1SIRLLjR9M+ulP9aCeBnM0JqzO3FLqhNlgojmNCmwz2MyxmDg8zmOhjOm5X/JSkrdGlJ5CInRsdQFpDnGoqUQCLoo5y8WS9qARMTIVPB+/+vWXWjHeWSGnqjXMK0VCaBh8Ncdbil1YdlJSWCGnCsDb0OuySjtelnqJRlFUTBakVrdUN5H1aL1ckl2kirVvf0Dx1b+dHkcUFnSQ2iOJSQdrnSubY9ct0TokfSVKH0/3UMwGjOtLRaMrVF9pjIBI5uWKgTsjEdBy36g+l1NeN9CmzDvVkTej1o4f9QZ0TF1zEDSaPIfrI1Ho/H+598nnsnT+ly+ARkrzhpPPIRIFeB9NoR3e1CyUMOvk3r2OiRdD9mYhfOPJ97fIvyvRUu6Dkj8mhDZUln9XUD0qdJAqvk5wLxD1PXTls7mm9EK0guVeCyizgg2jq260L/IVpKcuGzHrqLKMsH/JOX6edpZ7O7MzO7MzO7DXtDRtRdLwp50Zz5m2uBZ4ovcftTGDVOlymUUaIgs08dePIjMc6jzUaHXReCkBWtBjRkC3fXWEk4EygOc11Zja+Tz11HcsGPRdr1gX1js5ZVxye+LoY3RXpOg6XTIJCUDtBnIcw3uW43vCS1sJFQITFhfV5daHn+JXI6ZvXFM+PFKofinqGyx5PivZo+mrj64fSS6Be6CPKd0JfwB1GIg9vqyp/60JlvaNpkRYgCsVRZL5xAuuoTdp1irIjYpPBet1vFKO9Cn5H1WfcnQw/1Ug1Ak20EOFWu83CFwSEK/l9PrO6RBMtbypu00SLx3C7nfGF+hwLn/NceZudtP0qZrxcnWNsK2Zmxf12ii08xnqa4wIzasmsxxUtVpI33UVKJiADKLi0isdvWotdGYUlx/U9V09d/92O19xMkbVAUcjQ9M0K3EOCUONbkcUFWfcCpRQWqCphR2+NqHZ1lMQNlTqyR7dj3yXulkrdD+t9VLvrY5kmPceDQrUvEkNBTPcnAF69ZUGzA12E0wlBdRFAyNcQbiORbKp9FD3jgYkYE2kSyWN0m6p2NvW+GBP6XqzuO6Jeewka5eQn9HDaKF0BHAVDtPRgBNDxyE0aCtdSTGpWy1zBNIUn2NQrQxp/TCTbrvCtQWzs1zMpElktdbyLUTQLIhCDpipDNLjC9+1QY1uzM16SWc98UbAzGnC8fwl2FlGc2Zmd2Zmd2WvaGzaiKG3LtKzIbUsbDUXRMHYNRgLToqa0DYsqZ1RoTm7sGsqy6RuinPNMi6rvhi5MS9tYRpOKVeNwJlCkbUMUZufmtK3tI4ahOeMZ5c1mF3e29mw3+JMGHnN+kvKkueYUC9tigu3z0l0ut6srLI5L3KWBTnA9mOdlszO3s/nlFGWEdREwDr37DSigDJZt/sbud6wpoh9TGG8kJW07T4veo9ooaXT57e11NPSIpf3bVdJD6nLXc5A2UqeidLX76r6OqaXftjvVdU5bm6byFG3EKNolLdDuN0rFnYAFVXAg8JGjZ3jpeI9R1vCfPfUz7IwWlLLO+R6HklIi7xxdA8BHQ2lqfCgYS8U7R9doosVI4B9d/a3re5Wa/ayJtLUjt77v9Ffm03TtW+UTw2jRNUaVNfUlfeOYG0RfYtZF267psIsuVnsCQb/f/1TN3XevOxubiRavN3TWUxQ4uhvXzKikZy4I+YluFzKtW7RjvdbVjqSGu6gF7xTpdcCCdqJghu6+OAkq2ylr9mbTqiffr2NCX7B+uJgdrXr3SAKppOY5Z0IvTGVM2HCRhxDxjscts+HRiDo1s0kQTKOd/UN9ouG7145Yd1dLxJpIOapxou/6dLLC2cDxvIR8Lb+c5y2LeYnLWkyKIufLnKxYF6HzotHGu6hgDGMDTe3Ii4bctuRFQ9c8W0jLU7MHOOO5ezrhqdkD/j++dHvDThRbbsluueQPHvxrfuDWb2U2qlLnq2WrWDGyDZe2j2m8jmynTcFWWTHKGsauZmey5O7phDJr2RstGNma3d1TYhSsidTeYSUydjoQTIqa2ydbFKZlllcbI18mgdK1ZMZTpIL69Grg8ANphTQIrwdkwCRUE/Sc87lp+z6MyKOFtr1zJ4qLTlbcM8jl9YtS3o8sh8cAZi8H5s+AWw3TOwPCs8ellwb2uAmhH9i7+DbqfsQLIW6+MP0mj9GxcEudBMzKPHYbhE2lsJiIBAeAdTfIO5mHztOXaWCQNdqpx+KbgERw6WWMraGYVrSNw85qYur6PakK6uAoZvp83TuZ8PYLt7jVbHMSSsamZscusCgibR5yXmm3qULGpeyQHbSAvYoZrzTbbNsFHkMTDCZR00/2ltS15WRRMJ7qcXamS05XReqX0G5ckwaUjmFAJBKKiJsL+ZFRrL10BW8QG3Bzpc5oUmG4G2CzU6j2FX9//4W872bugA92GZnciNx7ry7Wnh/t9N7Qg456b9ux3s/GaApqdDeBOg4jVXJM2rGQPeRsdJ3ZpInMJCELa4JStJtIndFTqnTp3f5vUapxfaWSpkOr3exGIsFrN7KVkFTxpNcOcdIBSdY+Uo84M2EDOKIPWFxTyqS0nXno/egmHbdkA51WuFaJI1Hd7Mx5qsYxHW+mglpvOdg7pmpcP7k7q4XqEAw+CqPcEzqAVVClxSzRybTBMButm4u+bPwyV/J7WIl89ugcX7P3Sb6fL93OUk9ndmZndmZn9pr2ho0oRtJwYXTCu4ob/GShLGPnyxPu12P2ijlbbsVusehTRefLE3LbahrJVVyaHPOWnTsc1SVj1zC2NZdmJzTeMstX7Bdzlm3GYT3S/eUV2flDttyS68dPr4ujojxR1gRK2+CMYt9PnxzGttK3TA/FhybXIqvn6NM/U1tpmoOH6t/J49kqqx4CDFCd84wGofdqX89JxVTUy1rtq6rK8pxhAo+meYYKag/Z0MvvUzahS3HxSKQRijUsb3juQy6jNZ+R7mvI+fRwRNCd1rCzt+Mq6o5fbz9uAwUZxGLduavfpa59Ewle0zXOJhLIMrI1WaWIUk9ov5wzyyruVRPObc1po2F/Nie3nv/zxvv4U0/98/6wE1P1n/upecWnimsmLWMqSmn46cMX+MS9S/hgOLd9SmYCbTC0pek92L1iTuXVozxZljSNQVwgVB2PdCri2tDrI/tiLWwTB/T60WqHf+eddpeiowE3Xh/NQaDK9LpntWtY7a57SZop6lZ2UNku3TPQLI9WF1e7miraFe1V8bVBJpAfJ1j4wFEX38Ft9W9nAn4cVCyKwfNR+j4aLExLzGLv9XdMDCZFGtFFsvRde6+kuHxCbr2meIPo/XapfybffO4z6yEKmQkb71pn0axRr9017IERKc2FF+XSCuvvdsolo6xBJHJ5+6hPU7cJVt8BZLq0sC2X/bKxq1m0ed9nVftHOfvHrqaNlv1iQRjI9j3pDnnSHQJwYXzCe8prj2z7euwsojizMzuzMzuz17Q3bEQREF6Y3gDg+fFtmpFlZle8bXSTRSgoTMPl4kE/u65CxqX8iCZaMvH4kaGKjmLccuoL3lTcodlWiGNpGhY+5317X1AvPzqulIc00XIpP+L3Pfkr/MCn39efS2FanARyu65RdBrLj+NLAi00NjPNzUoSdrmQHfecQEYibec4pO3etau/V71keq3tzkxDz9LaNZtpE13ELWOfT91gxhzWKwbn9tiaQdrfI/WGvlK8CXPsrGfS7K+DHjemKMOPH4IhDo83EJvyeYIk+tg34Q0hva92zg8XPPsGxlI9z7axGBd4294rwLqgufQZu8UCQ+TK+JD79Zi3777CxFXMXMUqZARM6rT2GAIBQ52S8JY13b1PdYott+TLzl3v+Z+G3l9mPE2wLH3GfjnnyuSQX1xoa3pWtHibmkXn+hmCQJ66ujuZzu5yBL022UmknazvsKkH1z6IXsttobwf0/LI6RW3Qe++sV2CbHfRtMKXQbzWMZqp1kyyU60Z2AptCJNUx5CotaN0T7NjjX6s1Uivqz9k1hNaSaJRYFxIwJMEj821NuEkbHRd4/Q6GBsUTrut8Fjtro8KPzaRmKfIMqzrCl3No2vMLO2jEYV4US6rqf7Gzch/HbmW9yLLJOoco/CO7ZsAfOroEu/Yvtk3bj7M8vA4654LAI/RBtCHrDAticWOK+WDfvkqPYs5gffvfIHmsSLhX9zOIoozO7MzO7Mze017w0YUEfja6SfxCF87+zgeoRSvTWuPMR+FgPSUC7CezWsMJ6Hk+fwWHkOOzvYewRL7bTyGUhqaaPkB1hHF1FbYlNOc2orohWpPaSliFIUpdjoXiZogtsLpk1H559N323bOjl30kUgzjQzlW7925+P8zMnb9fc/xnn2eUKkDpAYnQNRb72K5zLwaIbaFA8v69dKeepX3ddgf7GDNzZs8hM9fJiHOKuGqKzHOVz5SWQl6jm6h/uHBuurjOQ6spPkMYYkVRqcolFGkwr/yW1+7/tUS2vosXV0G5m0BExfdwB9PkI0a1qPZF2UYB9aXkrDl88+i33VC6iQzlXI+mjjF68/hXOetrUYq01Wca9BgKrKcOOWtjbYuSWUIaGFAsWDyILN+y4SyY8TEqzVxjS7SlDSwXX0haLJ+ibNzgy9SE5nnShSyPU7u0wIp8QiHA2YkXrm1Y70cOSulhZyfZzyBEd1xiOl1wjgMMdcSAy0Rj1rawJTWyGFIsBy25INmmyl9BpRGM3n52WLALnxSOH7aMEk/qPGD557uoiTHjLf0b2IieBFr1klLA+g3gtspygsjAfiWy5w/KxVDZq07Ou2PwrArxxf5Ou2P7oxxnwxG45Br2bdM/jws9U9o0jg67c+1kcYX6p90YlCRP4e8PXA7RjjO9Oy/w74/SiT9meBPxZjPBSRZ1AFu8+kzX8+xvjtaZv3AX8fhR7/GPBnYoxRRPaAHwSeR4r3oAAAIABJREFUAV4CvjnGuI6dXsUskbF4VtH0D24pASs67gQ2w6UgER+hGVzw7uIbIivxlNLiEXL0oW2ieeQmZRL6m9ENbGNbkxudpLbdknxa02Shf1hjZXCzhhiF5jRHCk8+q2mc4quZNbStwUokFx0UtsYrDp+oIUJoDMEJY1Ol9FQ6frPZbWw867RPel6aLejI3AzDCWCdetK/B5NPx08z+K4nGhwO6g8XrlMx9eGCts4fw9zTGus/PNfHbWtaFT0yosVsX8D8ie4kNOUxTCsRZF3ATrBdk7YXo4OJMUG7rSWynS/57OkBk3cfUkqz0Y1rCJTSEMRg0uQRZHOi6J6P9WcgG6Qs+oK2aRmKHsKjL3V/XLM+VgffrVY5oRUtiFrtGN+aLqlbR5tl+N1GOarSvZtfVjrr4lDvUydAVO0qsCI7TYJeorThPUAgCnapDsaQXaCD1UYH+QPo5pV6W7eNot+1U518oqHvlDZJtGt0O933QeqynQSyo/U1LYx2p5e2Jb80JzMBW+k1yU3LKGvYzRaUE+Vkm7gaa0LPmND1G2i6yffvw8g25GVDvcixO5GsaMldS1gKHdt81TjMWP+wEnBdhT+db75dEe5PFLItwKUV46xGJi3GRerakeUtYgK+8DoOtfrbun4bJ55SGso0sL+eVNDrmSjKgVMyfM8D6wFiOHZ9qfZ6Uk9/H/jQQ8s+DLwzxvhu4FeBvzj47rMxxvek/759sPxvA9+G6mg/P9jndwE/HWN8Hvjp9PeZndmZndmZ/Sax1yOF+nMpUhgu+2eDP38e+EOvtQ8RuQRsxRh/Pv39fcA3AT8OfCPwlWnVfwD8LKqj/Zq2ihmfbs6xGmhllqYmSyHdsIgI0KTcRxNdX3Tsv4uW0jS85EtCSi8B1NH2hc1uvR274Nhv+obvH3+ejx5dwRnPO0dX+W/fe3PtgWLghUfP3z/Gk/hcfcCBPeZv/JZ/oh7Ec+vvLJFFKHg6vwuo9ze5auHKoBvcDm5ol3JJzm077orbQ8grkCjZe54aUTGjYWE4xnVjkYSBrGkXlEgkImu5V9YevSSIZldcT6eWziVFQMtXabhDJSK79X2hetnDDnTTPLTd8Lzz2NNKSYLNOgnkzvMdb/85QEP2bzjQtEATLbfabUI0HLhjStNwEkbcaWechJJMPBfdEWNTsYoZN5pdqpBxJb+PTZTiq6DLm2i5kt/vn6WToA13ABeyIyamYh4tIRpuNEp+9ET2gLGpWISCQz+miY4//7YPbzyDADwF/9PnfzfToqbJWhZ5QfQGig5SSs+TFHIGzXSR8a3I6ZtjD0pYXDDkR8oTFvUS9fDVZsDaaqt0bSOsznWghfQMmIgfqfBTJ4WapRDGLjsBr0i1L2SDSLTr3g8ZNI3F2sDI1kwnK2bZip3pktI13JlpJ3NhWv700z/D1WaPv/buH+V/vfq7+Pq9j/E/z38333blX/DD997DdLzCCNSt1SJw7SjzhpFtmI0rGFcYiczGFZO85nS65nr6qy/8U/7ejd9BjPAdT/4MVgI/+/nn+Vu/7R8BGhX8qavfhh9pFuN/+fJ/SBMdPLWOLvux5aEI4BOrJ5mYim9/4meVhj7d55eac4xNxUV3hEU9/nnMeak+YMcu9DkUpa6vo+Wl5oDz7pg9e0qOZx5zrjb7AIwTRHsYNQzPIxefgBbX+VLtN6KY/cfRAb+zN4nIL4vIPxeR35mWXQaGAN5raRnAhRjjzfTvW8CF34BzOrMzO7MzO7PfIPu3KmaLyH+FEnn+H2nRTeCpGOO9VJP4JyLyjte7v1SzeNUkmoj8SeBPAkwuTviR+7+Fpc/Yyxfcr8c8N77LF5Z7jGzDlltyr5n02+5nc+7UM0ChZHOfM3Mr7lZTJq7mLZNb/KvDZ2iDNj4t2pzSNoQoXBydcLea0AbDmyb3OGzGG9xBO2bRN0vNzIoc38NcgQ0I5GvZgTsmx7NlVo94JMM8ZRdBzJ/yTFjXCzo+pw3OmUny4GTtwW3Adgd1iA0heNae+LBuIC1QdvsaRhBsUEt0O+g4mvrtZd381TVrdTDfviYy2Ed060Y8u0rF+RSpYFSWcmMbGWybqFFcamojCrlttekp0zJYJm0fhXb3oLMmOowEZvmyj1CbJKqQi2enUM8sJH/LI5S2Yccu+n1096ykZt+ebizvoo29wXKA0jZcdEePzUt33uKF8Ql1cDgJ3CsmhGCULbSomS/zvimunslGg1u1qzlrX4o27lVgWi3Qdheyk+jN5tqMJwLNlhah23FqgOu1VNGax7GoCFIGJoNqrJFutaeiUENBoA2epkowLTy9/6Bvpnti65iRbbg4OWGaVVz38NT2oS5zh9xodrnsHrBfzrnsHmAlcNk94LQpuLx1jCFSB8vMrfB3SpguOchPuDw7wkjg/mrCk1sPcCZwPbvUP/cX7VF/nS66I0LUSPei1WeiFK8Ngi3kR/CEPaHBqF5NF1FI7P8e3rPLVu9nJoEmGqX9sQv27BcegciW0nIweqlfbiSSm2U6r5ON9UtpOSjnZAS++/rXMXE11UDTJpPA3Oc40TpO5R3wS488V1/Mft0ThYj8UbTI/cEYtQwaY6yAKv37l0Tks8Bb0FjnymDzK6zjn1dE5FKM8WZKUd1+tWPGGL8X+F6A2Vsvxl87PuDO6YQPXLzKS8f77GRLPv3gAhfGpxyUjnmbc2+lk8VNt828ycmMZytfcWc5ZV7nPLN9n1dWM66UD7hxus3JqmBaVlyeHnH1ZId5lXPwxCkv3jtge7RiN1/yoB6t6auBwzDuC0gnoXxsWgl0QOlC08dZHa0WTx9C14Cm0nw02KHC3UP6t11KpisQxyhkc6GOayW4Lirtu6Djuvu2Vxl7DC9Tl0rqBurh+r2Z9TIja8SWcgNtFqpFIvUOjCRu/I4NP0HW3DodZr+4H3WwS/vNTtapjGHvhpHE48N6cjKpe36xyvlcdZ5VyHgif8CePaWJDo9wp90iRMOF7DAh3ArutDNWMcMSOXDHferpTrtFFTIuZEd96ukk6PImWi5kR/1koOvPaKLliexwI/V0q93e2HcTXX/MUhoupv2sYsbttO+v2v/V9DsDLx/u9oOH7xBdmdJp23pdiO5vmSQ9dhORKPhS+g74mCbb4AYF7EivBCdxff9FIs04QoBqL/b794XyNzkJ2Fpo2vUzJt3/0t92JQQHX3/xEwDM7JKnivvM7JK3jW5iJPJLoxf40MEnmdkVt9odPMJhGPOVu5/hXtD3++PVk3zo4FM00WIJeAwTU/HPLr0Nkci57IQPHXwSgB+49gE+dKAIt18ObyEmNcNbXlODYiJ3/Cz9duGW3wJgIjWmheIocvK08IqfUkfbp5peLfWU4fvUd/fvUhRN9/BY8LjxIZO2d1Bebd1SGr5wssuizpgWa7Gs9+xf498cnidLBJfNY7q6X4/9ulJPIvIh4C8A3xBjXAyWH4iITf9+Fi1afy6llo5F5CtERIBvAX44bfYjwLemf3/rYPmZndmZndmZ/Saw1wOP/X602HxORK4BfxVFORXAh3Xc72Gwvwv46yLSoAjVb48x3k+7+g7W8NgfZ13X+B7gh0TkTwAvA9/8ek48BOHl23u86cI9quA4XGqBuXQtd5cTplnFyDbcX2pF7p3nbnLtaFs9ri24ezrh6d0HHNclpW1ZhJwH8xFVldF6w8FozqrOuDQ7oU3U35W3VME9kkr6hblWnUM0fHL5JH/nE7+domwY5Q2rxtGmFuvVScHBhSNWjWN+UlKOa6oqI89bMuf5qidfpA6Oj9x+ku1yxfUH24QgFHlLkbXEKHzLm35hfeA4SCNJwpvLZqd1NPQ01o+1QZ/GRv8Em93bXTG70+qVtHzzpgCpoC3QRysdP1O/b6OSlNKuI5vu60c7s9dRUnfZtz8fOP4KPY96+2Es7povp7s+PSOoC4xsw8502YMCSlNjUVgywE6+Tht1wIZJXm14it36k7ziYctsy8wu+7+HfE87xYbEUh9tDFNV0KW15htRpeq6B57LX1kvS679uem814lfNhoGhEypsqWNiJENSDJAO9LrH1MKr+vgR5SxNztV6LFH71c70ucjZCmVaAb3uQggdv18NEIolHupHUVMqf0PPusK7Ov+gnYrYE8NL5TXsERWMeOZ7C51tEle1uAW8K7yKquY8Zd/9Zv4usufYmZWvFBeT7TtkbcVN/pIovsEpe02ohxcz+e3APhBeT/vKLRkWt4Vlk9pKvR/+NxXs1Uo8PdvfeGDPD29j0jkr3z6G3sN747ROTj4c5/6j3jb/m0+cfsSMQrzu2POPXGED8ri2vXrPLX7gOOqJAL7owW/cv0i08lKIb9Oe2MWdYb3hmqVM5suKZLg2rLW+9npbo+ylmXjqFvH4rRga2tJmSQOjpcll7ePuHG81T8j87bgcD4idz6xa782zPbV7PWgnv7wYxb/3VdZ9x8D//hVvvsI8M7HLL8HfPCLnceZndmZndmZ/fuxN2xnNiRhlNYRorBa5rTRMnINtbeEKDTRMF8pfLbyjsUqx7lAEyxNY6m8wxBTF6xQv7iFeXrB8rQgv9ByOi85N52rPGMw+GCog9WCKPRdv6e+AKCNhvut5kznhyPYgVHecLTK8DdH7Dx3yMmipGksWdGyOByRT2tWNyfYKycsfUYbLEenSku5PCrJb2Ysnl0SRuqd322na02FpUVQzn4SY2invdBBVbtCZi9cJOsoJEbZyDd3vykOoKzGDArNHdZ0aBvhi3ahP7xKfOx2MYk7RfDSn8Pw+0d3pB/LvXXEMNTs6PLfkvKxXZHcisplxghPl/exB5F5yAmYxO2j3puPhibqvcxEJUk9dgOC3a3fRPcIp9OQ66nr2B7CtBepUJSJJ5MWDxvcUF3DX1cvWYUcK4Esabo22J5fqpQGj+osvGf3Wh9RZOL5x0fvIYxC36zXXx+hr/kUh5HTZ5IIT50kZ9P1s5WKENm6q01J0reIymE22G0nmBTyVMNykVAAQc8nOq2VmARqUO4mfUasJG0NMTTR0aBF/lVUL7r7rLc10vDRsKozHjRjVqmA0uXoO7nZ7h4No7GeXTmuizVdzn91sI6oexbXTj8j3a8HN7aRcYtxAVtrh7lp4eh4TNgXlsscv3JMD+acLgua2hFabXjM8hYjkZNVwXKVMcsrIrCqM0Qi86U2zdaVI3rB5R4fhXmV0zSW4A3lqOZkXuKc5+h4wmhcMT8p4SjjKAirccP+bM5qmdPMLKvlQIQqapTSuqRzE/4dRRS/aU00lbBqHQGhrfWmhiiqEBYNJkbqKgNRaoCmdszGcx30W51MCqeDRBMt8aklRGGytcJJoF06itRlu6oyRnnDos0Zu3rjVA4T4LzyjpNWQ0xZWOyeCo4AhG1F2+SZfta1Q5aWOAFTCZn1tEFTW3l6uGRlqc95Rvm607d7QWKUnvoDSFj2QTE7pRI6BEtf0OyL2REfZTBxpJSNxL6Y3aeeomixXmKfK9ogYkOPNUz7dMVsYyKBNQJJ0MnHe8EtUtG5Hr7UD93nh+g9Qi59Sgng/C81XHv7+jcxLMS70KfNXCLReyJ/wLPF7Z7yoOt3eTUAwqstfy17LZTbBhruoRJhEx1Wanw0/PiD38LX7HzqVdcd2ldvaZG2m5T+iX03dUr3xIe42zUNGGmmqY/FQzaP1HY9QDYz7YnohKVAKeStC3inVOFEJfILecQcu37CjllUssJE8x2c3sKuF8SkCVxIj6LR9OJPHL0LS+DJ8j5XV3s8P3qFz67O9/fpJ47ezVPFfXwUjtsRHz5+J0YiF7JjQhR+7vRtnLZFf4wQhfP5CXXtGOcN81DwE0fv1nOMwo8f679DpgX9jl7eB0OMet+XPtPlswaXtdR3xliUKqedRMJSf7Sf68uVWc/8pCQudLk5NVR7lnAgNK2lWeTqnErEOY8zgePjkdKy1AaC0ArMfUlYuJ6OhBH4lcPjmO3NmZ+WxMpiWgEbqVcOPxV8rb0j3VgI+iz6lSUWaZJ4VUzpa9sZKeCZndmZndmZvaa9cSMKFLaX2xRSpVk0tx4fDW0wTFytoinJqQq17T3Rdp71okadByJo2sIlIZRs3JAblTg1RsnEGm8x2ZpkDpSOGqAONuGUwc51DpYunPXSQxdjFBWdaYUYTE+z3URDGw3eGxpvoBUofX+ONvUD9J5+sZZtVDz7er3Oc7Cp3mrqTfhof/5B1gVlUfyrmE2acAbr4oFs3W+xwRGVhT7loCuk654PCub9sYV6OzKVSBz7XshF+k/d3tTr7XwJ2c1IsFo3jyZy5z0Z0A5gwQMPOgks5cZzGoWybMjEU5pmQ+sa1gR+w+WamvLk4h8pZiOtpqce4uGxKAS3J5JMkGaD6mcPLcdv9FN0+86k5aQpmZnlRhrFoCSF62PpdcnM5m8p8wbZVR6x1WQtLiQd3Fi0w12CXtPTLcEmGnE6KKzQpwZFogoFOU+b7rEIeG+IWSROPCSqfFxYy4FKIBaB0BqlRc+0M17XUUlSFfeJ/OrxeZpg8TuGTx1eYuoqPnH4BDvFkuDg4w8uE3b0Ha2C5aMPrjDLVlQTR4zCxw6v8Mz0Hh+9d4XCthxVJe89uEbb6jt/1I756IMrSgoZhY/ev6IiRR1YIkXIbdTxIkRhlcSj/MpindeoWEga3iCVwRCRlV4HkahRl09a5jstttBnOwQhn9SsWodv9R333mhU4tepVOMCed7S2qC8cAuLbC+hNkgjrMaZjh21QVrR176y1K0lpnsQK9u/e200UBvVTXs8X+rrsrOI4szO7MzO7Mxe097QEUUIaUaNot43ys5oGEBYG0OUlCOtTQ9d69bf2J8X8kwjgCwxR/bQSquyIHWw6ikl6KcR7QLVT8cfPPcRfv/+R/muF7+l96y7ApLtml5aizGaHxYTekhpiNrlaa0KtMgAbhrRSMSTvBiJiBuIthjwo4FH3mrOuROW8cWgIE2qUQBi1/Tnkgq+XQRhE9NqxwelJyFg4rqAHtf1DRHdX+/de+kb9bCPRjN2mfY7+G7DRJvsXCrQZ6ew2hN8uX5wszmsBgX5rrHPSFw/E8YzzSu+9al/2Tc6fbY5TxNtz9306g13jlvtdmrkij0V/Ks13NXR8nJ9DkvsG+6auG64031vcj3dabfwCAfuhDvtjEUCR3xy9WR/KTLxHLhjrjZ7jE3NRXfUc5s1MedWswPAxeyQv/b2H+23+ys/9UcZKnp2NatqR+tRdqXPoVJ5a9ToixT5ec3dhyBQBJwL1LlGDGKiFssLT1a2NGhULS70MObMeMjXFOAhS+9AHnBZqx59ps/kosm5+WCLZ2d3uTcf0+xZDlcjcuuJLnLrZMZT01H/nt09nWBngZOmJKAd9wC3j6eMihojcFiPGI8rbAKc3D6Z4qxnlLXcmU8Y5w3uRGjPSQ9lbbzVel8wrHymz1LHoVV6TOsURJHT82nFaYscZ9gEGY42NXsuHbFcRxSgDLXRGx1PUn3Ozg1+tH7P2tbQnOb6/HbvcyPEidd7UGXQapOkbww0CsWV1mw89wBtMEhtNBoK8uuOKt7QE0UMZo0Ljo+h1wWkMcSkhCWtPvg+akrHGlXNcka5/2NUPd1ueQiG3HicrCeN2luMdIOqHqP2jty2tMFwYE+09X+gAx29IIXvsdhdMRdQFFaiG29TyiwE6YvgSOzpyrvt++JzEKyJOglGnVisKJ24pE7akMV1R3W6TkMQUvRrQr4Q1mm67rd1E6IzgY7WO3ahcsfTn4rgMYhOgF2qSrRoGZJ+8JDuA1RhTtI5kc7pkT6KrtgO1FtKYZ2dpiJ4FKqdRwvgMf1G98DBdkVpW66fbnPgjhVFhO9pOTr0S5f+2S8GNBtR0UU7xbxPMZ2EEXlKR3U9FxsUHtLw1uJm35fhEd2PUQqPYQqrlAZD6Ck8DsOYXzx8E854nPH8s9tv58nJIf/69mXefXCTP7D/S7xQXmcidXq29CGbULFTLPpzHOpj2FVUuo5k3XOZLfS5aMdsgh1ISLKEfgom6qBWquqcK1R3vksnuU7jodSB2tqAd6mHwbS6PDleMVPq76xoaRtH4y3ZqKE9STrxaRJo06B9uirYLlZECyfHI6oLqR+pzWi8pnkVKWgobcP57IRnz93jC4c7vGX/DqdtQeF8kgywLJc5zTzj4uUHioC0gWZb0WE26WH49Ly3CeUYghAag+QtYgPNNGCXOqYQkkNZWexSASkxioIovCXMPGYwLvnG4mxArAIrjAHTUbI3WmgOUchcIIxbwt2CONL+B/EDMk5RypUoaEqqmxja9ZjX9c2EKNhKaDPpaeV/PXaWejqzMzuzMzuz17Q3dEQBa9ideMGk6MAaLVj1nrVV70uFfjSsxEsqoHYF7QST9AZXKoFWDBo+m5SSGWc1d+ZTspR6cmadjgLl2bnRKmW0L2KfzjEu9jO8sx4RR5a11N3s3hV9o6pR2ZQOilkktusCuAyK7zEClSVEem+/HcW+mB2LiLFBPRV1axLElX4fACbrlMWCKqglwrcufdTBSg1R9YhFv+9TXimaULdUCF76Xg7ysAGx7Y4bUkTU5uncm3VU00UV/d+DUFmiiuw0s4TBN6lPpLu2JiA29r0f7W5LaZRo7g8++dEUPbSsYs6NZpdVdBy4k8T1VOARXmmUS+iJ7EGfehrSjO/ZU7wx/bqgyoR5KpKffBGacd33musJ4FqtNNF77pTfuvN5qpDxa4vz3Dze4mvO/wpvevouVgKLUHCrVT6iZ/K7vbBSg+V6swfARXfYRziGgC8FX6QeCtGua1BywE5A6MpPHXPtg1vEoMuiS95opmmnEIXRqKbIWsJI072nxyNWdcZoXPVRZ/c++nSvC9MyHlcs5iVjVxOySOkaxmWNs4GRaxiNak5sSekaRkXDSVNoSgpYnBa0W4ZQBFhZ6uAwJtBGQ5E1KbrXyL4wnnPZCV9//uP83dPfzu/Z/xV+4NoH1tFyFNrKUWzp+baNo2ktMY99es2gXEgxps5qRHtAMn0HYhQkKmw4WsAmLW5RmvVOaU871APmxCKTZi2AJCn1ZtdEm9mpodrz2JVR3XE0Ig5eyRy7+NqshDDSCEdIkX2m73U3rpkmdXC3EI3o/qLuV9oUUZzBY8/szM7szM7s34W9oSMK67SLsetEBnqYZdepqulaheJpdzKa/2/MGh7bTbMRfKteysjUGKsSipkoPHYnX3LtaFv3m6IWgCZFFAHh/7rzfj5y7cmNXKDLWnyC6Q3PL1otyNNKHwUFhLa12Cx1raZmtK7L1iaZ1hAEezLk79ZGJqUk9v31aJO0o0/cO5j1OQD4h5rdtPFoXU8JUbBOc+aY1O2cinsE0eKlXmIkC8RmU4TIJFhkVzPpr0GKgoZQ3uF50e0zDJoIUS3mbj/dOlpgD3ofzVrz2IwVNjvLVry1uNl796U0PF8obriOtq85AOwUN/rDP8z11C2bh4Its2JSvKJF8LiGvma25VnTaDc1a3hsSc2OfZTrySO8UCqR8jwUXHRH1NHyueU5xkXNs8Xt/tilNBs06B08tpSm5zpaxYz/9Bf/E5plxu65E7o+yc7yY5VFLe5H5pe1DnHt92wphXsqWodWEkw2gR2icH52ipHIrKh6JoQ3H9xl2WYYtL4GColtoxZVt9yKC7NTPndSsp2tiLm+T+enp9TBslsuaKPhOJuyUyy5fTqltC3nxgvGtkZMgpbbCFlg1WohJTe6zrLttMWFiasopeaZ4i774zkvlNep/FfQtJZJXuMxxMpgZ7p+DCpuhIkaBadCtA9CbLU+0dVKQmPI8pbYmKSNbdWblyQvOm3xUWsUHf0+GYTdBhNE38dgcJnvIfLdM1ztBrAJ2BLWw4akOkQYp3oc+pxbG2hbi6uUdVeygCRIvnQMB4k1GdExSQKJHl02H4Yvwc4iijM7szM7szN7TXtDRxRZpl5g53WYhPhxElgFFZ0xlTJZuiQ6st54LZ7eebKuaIlpxncmkOUtuWkpEr7whdlNfvnGFQqj63XbNd5iUO+nDpbqtEDGimQyoqiRpnZk1vcNgpOiZm4ScspGikThEaLgEi+LFOqhl4n2I7d+3QyYeRa7DbnzlK5RqGoWyGwSTcoCwatko3RQW9hknAVckdBfVmgqR2wNpmzwQXpKiLZyfS0hZqGvUXS5247ywzptprLpHM1RRtwXzXl3QdugIS5kCfo38oNGuwEySlRHQ9I9Ck7/7sWMZM01pNtoTaeDIrpMUSjnsxMWodBmzIRCGvL+dE1tQx2QjuupjlmvReERcvE9H9EqZMxDQWkabFxzPR36MaU0PddTiKY/piX0yxs04uia81YhozQ1q5hRB8eXn3+ZY19SmoZcVMdgEQZcVOmimrgu5KxihrGB7FaG3zO4ZSS00suRNlOFtvpCEB9pJhpl1Ftgc40mojNgItW+wbSWvGh4797VjXfv6p1dnp/e3oiQu3ep+/e57IT37l3lpVf2edP4LlJ6nATes6fMrVVwPDl6wOevHfDs+C6fvnOBp0b3uTw6pDANo3HdvwdiAwEhs4HnZ3ewBJpoaaLlxXDA2NQc+QlNfMB7d6+yChlfdfFF/u8Xv4zz04RkC0K1ypmUNWITvY+NFKOml/sNwSBWqXc61JMtEix1rjUNN1/XcUa2xi8t5KGH1JssaNPe/Rx2awrb9s/9osqV8qNslLpj2ipyaQ1U65/9oe8vnr5R0Yg2KvZBtacXAuuyKNFoY2CIgl2KIgw9G5LEX4q9oScKZwJZgrKSKSGaM2t1uUyCXuCQIIPpwoagA2jXI2FEX96iaFktc0ZZw8wq3fDUVpSmQSTyVdNP879V/4Eew65J15pgyGyCo0bBli1hqUWx3LX60HT8LxJx1iueOosURdOHvUYCIeh2O5MFy0px3B0HTRsMpWkw6ORjSk+RJh5beIKT/rpg1t3moLjvrnO5K8QbibSZ5TkqAAAgAElEQVQLB1oHZTSpWDwYpS50vVhF1tJOK5wEzMIQdlrsfYe9HPGVJRvXOrnGbmBODy2RuKtFSy26xf53uo5TJ1MyPUl9I6AEh2GYfRqo9klMD/9Dz0E3uXS9Gy5BIjus+syuNiGjErAx9v/uP1NN/uHlNsb0vUkF5O758uzYRb9uZ7PHKBTq+m2/z06kykhIBExruvFcPP/xuV/sRXGGHeBdGmoVcv7FyVv6FGtnt1ZbWBsoXhHC24XgZIM4US9YIvdL4IB6Wz9DpmSHsfSYLFBHYbeoeXBnxge3Pr2xix/5ta/gqz/wqU1teNbcWQBXm31emH2KHxu9wPvHn+d/H38AI4EPzjY5rH50/E5+1+wz/Gh8J185+xUAPl1dZpTos13Z4FtLGxSS+zVbn+gndCuBn7v+HJnxPF8ojfgHtz7Vf/5g/b51mtJqHs6aQFE0LO6PsZOG5UnBdGfZX0eb6YDcBEOWeerTnEVrYLuB1hCdVQgsMLY1490ldZWtxxMTKcqG5rw6QCPb4FcW32TYcwvcpOmdtXxaU98rN1KEMaKpP0/fR2Wq9fMUYyp0J7p+t0xQ9nSfTUcfLzoeRafpKNOu1/lS7Sz1dGZndmZndmavaW/ciCLNvk0HY8t97xF0M7szHltr2DXsSg5Ri9m5aWmDJRP1rnfHS1Z5w8HolPPZMbvTBReyYzJRWvFMPLFV+ujgDVUqlK1aR5OOGaLglw7yQO60yLVaZRQ7GqFMspqqdZwbaWFzVlaYceT+fMx2vsKZwOn9MU/vPuDcllKc35+POZid4kzgnDvFGU9VZZSjmiYYtqx68nnZUNiWidNCYJ63VIlnKbh0DdzaUw5RyGca3ufWsxDIpulv15Jbz3yVs7w5pbjcEna1GBwvaCHYlW2v1YxAlrUsF4XCVCVSjNUjJAtItvY0Yyr8xWwtKgTrlJhB4X5ilJq6p4DOoJmqdnbXhe3XjMqaBhm1PROotYNUHJ23q1GBNY+KDinfk9/wkrt1DYEga64nj2ClfnQfBLJBMNHzNEkgYx2pdEVuPW6dtu2inKaPXF6N62ke4BMPntiIKEIU9su5MvYWCvU2OUxuBqp0bWOSq3VL/Xe1oyJFXeOitUGBG1sL2pmhbh1PP3m3j4Y623v/7Y30lyds/AbSb83FsztekknLua05dXA9cKDb7tzWnExatkar/rsmWrbKFZOs5mDnlJNVwf3lmJ1ymWjaB7maZDOzfES4aG9nzo3jLd61c4OdCydsj1YaUcw87WTJ4WJENtF304lmCTqaetBrmE9rLuyc8MrhjLa22FWG5BqBXs4fcH7rlNrbvjFXTOBgpsvq1pGbFrGR0c6cMm/IkogQwKXdY75wd4RpBFsloSgBScwN3Zil6Vvp35HsFJotzU91nfTuNLUEeFHQSWrgcwtlZiDCYy7b67LXFVGIyN8Tkdsi8snBsj0R+bCIvJg+d9NyEZG/KSK/JiIfF5H3Drb51rT+iyLyrYPl7xORT6Rt/maSSz2zMzuzMzuz3wT2eiOKvw/8j8D3DZZ9F/DTMcbvEZHvSn9/J/D7UK3s54EvB/428OUisofKqL4fjQd+SUR+JMb4IK3zbcAvAD8GfIi1VOpjLaK8LGOpyU2Ly3zyNAIhFZUsAbsEmWrzT8diqr9cZTHnCco3NjV/+bl/2ueEfTT81Tf/qArfJ+/iE6snyUYNU1vhMs+srBCJLOusL+DWwVHMKupV1guZzyYrxkXNdrHCiefO0ZS/8NxPwBOP1xkwT3RssomJVgJ/7l9+M1cuPGBml4xdzbistSBe5Ty3fZe9nXlPPTKxtXr4zrNyCa7XNcGFASUHUB8V5HtHPQ//ZFRzeH+CMZH90YKD2ZzVSGVls7LVwnbuGbmGEASXaXQlJjLOmz5ayK0nS3KOJvdYl2B9JlDmDas6g0KLm6HtvG7NH9cJStzlanspVKveUjteR4iC1iyMqEdoEz0CaFQEUAXlWZrkFXW0NLHgTjujiW6D08kj3G+nABy4kyRqX3Dox30hes+dbjTiNdH1kNWO6+lavY+RwI5dMDOrdC8td9qttO9jMvHMQ0GIhntej7lvTxmbioDhXjtlFTNKadh3p7xUn6OJVqPZaFiEnJdu7bM1W2ozmTc91YuKQSn0OjuNnF4eQDJTg6LSenS45PRhAtmoxUrkv3zLT6Z3SNd5qT7of2cunv/iuQ/zUn2AFaUg6SKBefqdVgJPZveoo+XPvOmneak+4M8++1NYCcxjTobv+bL+7LM/xdVmnz/37E9RJwGiZ/M7/OdP/7/p9DbrIC9WF7k4uG/f/cIPY4lcb3fZMitKaZjHnHvtlO9+2w8rrQme3/nCZ/oosbP/5td+H1YitVdBssK1BK9UGzbB0Ov7JX/pfT/In//YH9LzyMDlWgg47475i2/6sX6/f/rGH2Z7uuI73/QT/TF++vgFdvZOGefaJGhN20uc/qVn/x++/Vf/ONFFvKwbF2MAu5SelsMupdd7iQlarxcnFakl9sukBevX6/tCIwm3kA2qli/FXtdEEWP8ORF55qHF34hqaQP8A+Bn0YniG4HvizFG4OdFZEdELqV1P9xpaIvIh4EPicjPAlsxxp9Py78P+Ca+yERhJDIuaqZZTYiGslCUSSc0BDo59Nw24gn5mrBOnHbs1saRGc/YVpy3p4krJ3AScibScBjGhDSZ/PPDt5Bl2oHbNFYHVxPYHS85XJaMc00LNLUjK1pmRcWF0UlPGghwrphTXmk5b0/WlNUD64qgD9NX/7Y3f07x6QRePDzgreduqzrfVuTuasql2TGlbWiDYWRrXN4qh5/TInAo03G88kPlpqV0LTsXTmi85eLkmJ1ySdU6ZmXFNK/YynSQK51lZGusC4Soaa42GqzzfRd5CJbzk1PCWDiuSu4vx1yYnRKicFi0aQA3vfZ3462iSdKkPuwx6QrpoFh+axTNFq3+HR09Xt2Xse8Sd0Z5hyajCh8M58YL6mC520x59/gBmbQYAhNTbVB4d/0S8Hiup25dYIMbaqil3d27UhqeLW5TSsMqZr3TUZp6Qxt7eO87rqfOrAR28sVGmusTJ1f47PE53rf/Bf71/SdpvOVg74TjRUnbrEW77tkxArSFDhLNRHqeLxFoRjrBdhxPptVubdPCU3sP+nM4b0/Se6a/+8AdbwgyjV2l3FkpzdN9NzYV+4Pf06AT6UV3OPjtun5pGgUDEDhI17BbnrOZIxleiwN73O+nQ5eFaNgxi/6d2ZGWg+Jk4/1aRYdlzcYAcHl6lH5nZOUzzo9PuHVvu3+mtqdLVkXDgT3BJk6oZqKU9THq/e7GDYumh57evs9Bun6dPbNzH4CXDvd4Zuc+L947QIDz9lSdoYdISsUk/q1ErLmhUy6RtiTxp8H4psCXbSIAfRHJTrUvK4p2kjezuMF08KXYv00x+0KM8Wb69y3gQvr3ZWCIpbuWlr3W8muPWf6IicifFJGPiMhHmqPl41Y5szM7szM7s99g+w0pZscYozxM+/nvwGKM3wt8L8DWWy/E85NTDlcjnttasT1aUZqGyq/lS8e2ptkCIgp3dYOu6JVly61Y+hwnnrcWN7nut/HR9EI1h4xVyzdqKuTuaoo1gbeX18nzFmcC46zmqNJoYlZU5KZlf/cUH4Sbh1v8kSs/359/HR2l1JRGI5XO27zjt7jR7PTMoEYC85Bxq93mlXabZ/M7fNXuvwHgvDvhO9/8k73O8ipkTEzNSSgZm4pVyPjV1SW2pyvtPM2Uq8a7BCMutM8ht55lk2FMoHAtX7X/mRQ5hT7FMbSJqfip/K3kWYuznt1iweGkpG4dde2IQfi9BwpLtKy977/z4m9jNq4IETIbOF6UXNg+IbeeQ1MyyyrlZ0o9MFYiDeopGRfwo3V/RTSRZlsp13va84E5o4XYZZWzM1rx9Rc/QWEammg59GNmVp2LEz/iarPHwhc8W9xONOPK9dTxND2d3+2jghvNLguv/RJPZA/0OseSz1fnKUzDgTvpacZPQsbL9Tl8NDyRP+ihsk1wXKv38NHwdHF3g2b8auJpejK739/DV5odFiFnbGqeyB7w3q2Xec/sKqvo8OFp7h5P2Jku8d7Q1hbjVGDHbYc+NREjjO4Gqh2TrmnEeO176TSUmql6ns008g0XPtZfy+NQkounDparzT5NtD2/1HC5nve9PvW0Chkv1ecopeHJ/J6mmELJrVZ/TylNz6O1CGOupjSdJWwsv97skonncnafDO07WcWMF6uLZOJ5Jr9DmSL+XDwfWz7FrptzOVN+rXkouNXuEKIwsysuuwd9/8vVer8XsPoD538ZAB8lSdEGrp3sYCVStS71E0WutztMihorkWMHW6VqX9fR9uOG6qlH/sD5X+azzQHnraYv3zG+zrvG6iP/1ze+lm96yy/z39//aiJw3W/30FhTd8XsVJxeofxqnQ3c+h6bI5FqD0o0sjASsA1kC6GZkJhnwVaCm/PvhT32lZRSIn3eTsuvA08O1ruSlr3W8iuPWX5mZ3ZmZ3Zmvwns3yai+BHgW4HvSZ8/PFj+p0XkB9Bi9lGM8aaI/CTwNzp0FPA1wF+MMd4XkWMR+Qq0mP0twN/6oiduApfHh5S24bTNeWJ6xNSuOFecsvQZRiJTuyI4lXEcmwopFZbmg4EsMDY1mfF949R3fuY/5GRZcnn7iG+49DH+4Utfzh955heoUgVo2WaM8obz9oSmdjw1e8D9aszBaE7ptBHu88d77I0WOBPYOzfnbfnNjXx0V3Bfpa5SBCbmDs9ltyml7dctbcPEVDyX38ZjuOgO+5zsZABVnEdHTqDGMJGWVSqmXpodY4h8/GikfPpJNrXThchNy95owSSryK3n+Vyblbq8/fATNDq4tHWMD4bCtax8xlZZkZsFLze7VJXlbYknaQ2ZFN5xcIvjpqTy6q3tlEtyq/chs56JVU6tTtRp2DwWo4DRhkNntHEvuIgkLw8vhDIgqTEqNy2X944U6lwseGtxg9I0hGj6CAwgM0teKK6ny5G0E3qup+sbtYtcPDvF2m8Zrv/28npf3+hy45lt+bLRFzakUH3M2LFzdkbzjdpTVxcZ1i66fe+X1zaWdTxRn15dwZrAznRJ4w1tY4m1xVx3hO2QitoBaZW3bHHBJIhxOv/EAZYfRRYebK01DFsLbytu8rCV0vCu8upGfaJb/o7iep/vb9L1LaXhvaOX0nOgeh96DW9sRJoApTllp1wk0MB6KMplwV552q/fXbNSGj4w+lwPfe2uXSkNv2PyGb3eCR6bWZ88ek8pnsNQkKXz2y/XnFvd+VtUs8JI4InpMXWw+MwwcnqPvvf67+byVJ+tI3uRK7ND2qBd+D906wOMXd1zQ70jv7FRX3xPcXXj73ek90SAv/ZvvkEb4xxsKOVKxFSkLAgqVRvX3219PnDnvaINtOlyVGlklVabKO0yMVLnGoG4Jaz2H7nFr8te10QhIt+PFqPPicg1FL30PcAPicifAF4Gvjmt/mPA1wK/BiyAPwaQJoTvBv5VWu+vd4Vt4DtQZNUILWK/ZiEbYGIr3jd7mWqSUZiGRci56I6YmSUfmz/VI5miBSI8md8jLxtWjWNxWjDaXvHm8hb3mgkjm9ITp2Oc8xSu5UE74fbdLY6ujHnQjrGmQ0YoWqMoG945u4Hd0gnHI1Qh44XZzR73XhpFX2Ti8WhY3i0H+pdvHnN8NOzbU30pEu3DPT8lYBhL1Q94i1jQiL6Umei5IA2HfkxjKlZRFde+YvfzAHz65gXy3FNXWrQn0SVnEv5/9t481rYsr+/7rLX22nuf6Y5vqjfU2K+GHug2FN3QBuOmhWiMwThkgABBwrHjyMhRFFnBUZz8QXAsy0nkiMgysVCUyDJxIGCmGAMWhMk0XU3P7q6pX9WrN793p3PPOXtaa+WP39rrnPtedVFUN5HLOj/p6b677z57Pnut3+/3HfjG0y+iCRw60Z5uMUzdIH0pe1QJSCniAztXqH3G0DTpcz4oXrm3jR0skUNtyBLz+PJYmu5znyfs+Krcg1bixdz/bo3DuIh6cgpyKUcJByQIci3KLWACaMgyh/ciNf3VO1dlO/HaVM7ShoxSN2kAa8JSCqOMAn79wNCsvPB6Y6N+Wd9o7V9sB25IE7LUvO2X9/IgVnXksdFa+TwtlwZsRxslQ9JLNm678jlQnBhQcuVoguFGs8mzu69S+4zfufGYXCOncA9X6JsFdZsxLFq8JUnU98xstcIlmp+Lvs5FwCCudrOwQkpZjTcqKse/2dh8btFU3iYJ9P4a9stABkI5z0IkRyIgYKjq5TX3RsQUVXti4jHr71vctgsar3QqlaXSWDDshbHIwtNyx22kZvfqoDTRCwyBCiNS8jjev31FHA2jYkN/f4bxTf459RRft/UyPpapP7jzMgC/u/c4ALMgz9xyEFryOsbDmqkv0/739kegoNiPEvCrE6WVt7Nf0f8kKBanNaYOeKC8G++vW0p4ZMcrTO9oslSdksHjrcSbRT1975f404dfZ90A/LUvsZ2fBH7ydZZ/DHj3mzmWdaxjHetYx/+/8bZlZk90xZ8dvsDcZ6lccb3b5KuL63x6Lq2QXHV4K9Cy02bKxqgSD96gKG3HhWyfgWkpdcuV5jRNlZFPOjLlmLqScthQh4yZK8izjqrNGOUtn68fIs86vnks+jel6tAqMPeWBpOawr1lZRUyStUlZq8PwtVAycyoDG06L2nsBVD+BMywVB0thgaT4IUOTY4jx7NrZiJ4h+bp4noqA/308H10XjOO7NN8U6CjmXZ8w+j5hDm3ypEHKQUd+CEbujoBI3QoPjT5HHNfxOavSTOzn+vey3DYS3FrjGrZ0lJO6XV95r44kX738XvHlxkNapouIxtEDajIQLVlR9uKvo8moHInM+h4XGoQ+TJGRNgGpuEbJ184ob1kcZSqPcFXMcqnrK6f5fZaT7mSZf02ekZyz8xexeBPdJXW65evMpiNEqHAXgTQIkzm1c9o5R/YxkgL36OHvC9nyvB14xelsetzPnHvIofW4xYknape36qXCFdRMyioaEubiSigjsJxySY3wC/tvw8X1AnzITkP+b1/rvtlq/Fd28+lc+hLaqvn1du+ri7vr5dFBA9X18/VUvgwPYcRruyRkmj/PdFqmb1A/x1SDKn5v/ef5fpikz936tMCQw5aajNIuSmx4VlmL980/tcpA8hxK5mdfO7/mH6Ebx59njZoDvyAR+1dHIr/9+47UAp+7uBrUtbs0Ezbki0r3wejA79w8L6l0OWxFfOzzQdZ0z4DeiHT1a+OCiL2mMn/uzHkKqQMRMVnIWgp32YL4U9svByYPvrWutlrrad1rGMd61jHG8bbNqNQyIyguG8YtmpZ+wap8/WSwI9v3SNTnmYsct4G6WOcz/f5Yn0aEKtSrcRcvV5YWi8m7q0zzKuC0nbsdWPOjI8ThFSrgI0zRwK4ONs5oXtDSE3PZc01zmpOaN8sR/wTiqexd2GCKOGuzpB7aGk/A12Ft17cPCRTji4YRqbh/M6hkN2UzNREg8gJi10tDXLsyqyrP+YcR6s6IUOppY7RE+fuUEfzlH42fv/n9coRr7LfjfKcGR+nbRVZh6+W10CVQqLMTUdWdD1RFWsctugIARbTEm09Z/Jpmn33e+t7O46lZpL4Ry6PL13jqPW0GnI+/Tpuhfjlsfqk/tEyTi7vr0W5MpNenVUbVv8f0uz7fkXWVeVapzqGtuHszhE3ui18p1FFSDLU3SigTEhaWEnePbLZg0KMqDKFR2ajn9l7KB1HPyMe2JbWiXJrL64bgDLrmNiavWoofaWdVa2n/nshUOu819CKvbd0XWJmapXDBL+idbVcv78+Dh0zh15TrZeDd/I8ak4s779Xn7h3kQ+efjntU553f+J3ubbSZO8VfXt1Yascugcq9MfThpTNjFST1umv8acPzkvvJCisdmwVC64c74ipk9N8fG8J/jRzjRt4dEvq96iY/WVzEvjETllaBiioduKdUMsmeDZbWhwrL+RUHxTdIJAtFLPzimLJqfxjxdt2oKhDxoHPT3zRNZ5PNqfi/wNNyPC52EZNfcnfOP/PU2NKK8+eG2N1x/lsn8/OL6A05FGiuvaWnW0R5btTj+mcpm0NZ4dTJqbiRx75f6hCxoEfUvmcC9k+peqYBsuBHwJw4IY8aqXTVCHNwmvtNrtRBsIQOAiD6G2QC3tXz0G5JBtxvd3mcnGTkWoSDvzAD5m6AeftPjmOKvIEPDrJFYx0jUPzwxd+HVgK3H3n9vIaHrghI12npnUTDFM/WGne1bTRL6EKlivtKbbMnKOgaTEcuBFtMPzVS7+Z9tEEw9wV4tZmhY3byzXsuTGVt5yzh8nv4YniFu+6KAifn7r5fnzQbJYVRudUi5zhWFBZpWkZDRqa6EFitSPPOxEXHIic+TuKW6mp2TeWX613MYicRu9C14aM290GPqgkyTH3BVa5E3Ia8oI33OzEG9vgmZiF4PfdkCpIg37LzNFq2UTtr0uPyJF9mhPbLnWbvCh62ZCd7JiRrjnww9QoBziTHSVOx8yL/MjpbMoPXBCOzt+efYQ8cxz4MXVl2RhU6FalIU88lD2ZkQFeaU9v49yDPYKB127sMN6a49zSp73MW2aLAmM8g6Khbq2IDWqP31DcOx6ideCTi0ce+I6uNoLvHyQA3lle42a3yV43fl3uzioiCb60akG/n7401v99oiv25gMc4kr4ycUjD6ghrJYKT2fTdH/6/VfecttNyJXjfLYv6Kix4hP1RdpgeDq/wXPVo/JCDuLuePt4nAaN1hnGp2vuHI9omoyuFd/vdI6NwpfCntZuiU5LkS0FMVcjuiCsXKso/If8DPo+FFWA8l5gcXpdelrHOtaxjnX8CcTbNqMoVcdp0zDzOjXbcuW42sgMMjcdc58nZuOV5jTfMnqRdqUH9+lKUsBSt9ReRvoizl7boHls6x4H7ZCLwwN2ixn7m0POD47QyrNj5uLVaw4pMpeOoVRtmnlcyvawyjP3lqFumdAw0VXiO1QhwwKnI0Z+7q2k4QRK3XJGHScsOCAy1QTOmWMqc0S5MgMbZcKb8CjaoGnQlHRsmDqx0e9vJlu19P2uYsljy8xPzvziPiZZlWZqc19g8FzIJI9dxdL32zDIzK5B+CIjVbMRBfJWZ3GP5nfT/jZz+XvjDeO8YfPsXWHK647jtuDsZIoLGk3glb1tLm4dJo7FrM0Z6prRiny4xfFEfitpAfXudqVuGdrleh4NMbNa9bXuWfqlvXOCWwGwYSp21TGWk2XAUrXpPGE5Cy4RzH9fUhIIsjyMW/lJHsUsFFyy97g/rOrY0nN2V7WFgHObMhOeHg+YjBciZmcDvtX4LM40I8bflZ4MaEeIHLUOkMlPO2jTrBfAO8V4UJPnHfPjQsQcK4urRaerMGL05Y8tv7HzZDrOnk9Qu4yRlWlt76vdOkMRxRrffeEqj+e3+emb0vzNtWOYNRx3RYKiy3JZv//9qCkpTSdZnHE0znD1aJvL23eYdzlaeRqf8dTklhyHz7jbTvjk4YX4fGWiUgDkpkul5v/8wr9IDev+vuXKs6UX8X5FR80MfmXvXfiguXT2Hr9275klPws4mg7Rxomcu3VUzlJVFmPEK77psiTe2H8VgjlpyKVUID9awpm7ESegs75AKqirYoC9yVcEKrTjWELU0A0D7UQ4FW8l1hnFOtaxjnWs4w3jbZtRNEFztRtGhU7HSDX8/vwJLuZ7fHjjs1yZ/xkOu6EYjKjA1Jdc7YYnyDZVsJEMZamjN2RhOgZGGqD/zumPs2OOaTEnVEZnvqANmipk3Oy2uNNNeGd5jS1d0WC4E/WCDtyQR/O7TPSCA1+y58b8wr338cHNF7nQawZ5m7bxaNQXsqrjwA25GTZ5bvYYH5589gTD+Lab8JnFJT44eoGJrqhCxj03TiSwS/YeI10zj8s/tbjEqeyY95RXE7T1WrfN3Beczo7Y0vPUo7jZbXKj3eap8gYTvUjX63Y3YeoHSddH1t1KtXggQSqNCul8YJlBXG12udVu8u7Ba0y0MH88mpeaM+x3I57duILBozeXRjwAv3bvGb799KdTvRuAZd81xXPzx3imvC7QZF1T+Zyr7U7SbhrpWghuPuOV5hRzn/NYcYeJXjD1Ayplea3ZxaG4ZPcodcs8wM12k1K3vFid5ZnBdSpvY0+jO8Ekh56NbFIWt5MJibIKllfqU9Qh48ny5gNaTz5oHsnvMtQ1hsDn6/PMfc55eyDbW2luz2I/pY/vekg0mn5i+qex0azJLBRNbQgWCNGQKNpjgjQ68Uu0aMiEuFhXOa6KRuUROTA/LvC1qCW7KoNGM9haEILC14Zyd8GN6UY6ni72OB7Z2uf68QbOKyZFw+GiZHNQsbcYkhkn/b3Ocu1wk0lZs2gtmXF0zrA1WLC3KKQ1Hmfqm0WFR8yZXj7YxRpH6wx1m3FuMuXFg9ifVIFZnfPQ4AhrHAtn8WHE9eNNlAqigYZojxntxZTMOO64jROqBP2z21/3oVpmoa9Od0St99SYm7MNMS7qew/XS7ozNUoHbN7ROoN3hqKoyW3H9GjA5ma0vZ0q2m3JBuwMvAqpTzF9RCWZ/Swmur16bFhRibfHK6ZUgCth/FpgflaJLlorOk9dCeZBv643FeuMYh3rWMc61vGG8bbNKK7V2/z969/CH756iR9897/iuzc+zr+78Yc8V1/gKXtIph1zn5MVS/Oa//7Vb+e4KSizlkx7vvX052jjLNoHjWsNm8WCsak5aIc8nd9kopc6PtKD8ExDRqkcNnhOFzdw+c3Uo9jSFVt5FbVjdCLbVSHjcXuX/+zcr1HFmWSpOoz2nDHHXMj2BWURZR52zTGl6nhy63ZEHWVJ0mBLzXliQ2rYQrJznMtEV/9Cth8lQwRGu6UXvKe4kWb7HgWqYye/wWEkwdLbvYEAACAASURBVKUeiOp4Mr/FE/ntaNQTMBHSe8HuY9hL19+qjidyqQH/6EvfQe0MZdbhvOaJzbv8+Z1PJnkEh2KkGnbLGbMiTwgeFzQTveBdxTUoTt7fVZTML/v38Gh+J/1tFbK72nfp1U17GYhJ1HQqo4KsCzpq/7S8u7war4fs47Q5wqN5d3lVMs2IErvebrOTHfOjn/12/ta7fglD4H988cMMrGhl7S2G3D0asTESi83dwZzWGRadZdFa/ovLv0qpa0G0Df9oraeenDbJF1TB8kv77+WTdy8wsC3HdcET23eZdzl7iyED23KwGPBjT/8sHs2ZyTFVJ1ItIQOVe+lBIJaeWbSf1VG6Aw3BBFz0MQhB4VsNrYbMY44MXABbdNTHViawTqErnexmaeT6TefLG+jijL3ZMEznJSHAqeGc41lJYTuOFwW57fjE7BF+9drTHM9Kyrzl3pVtzj5xl+NFgQ+C5AGY15a2yWATJkXNvMs5XhQoFQSVNS9oRnO2ywVX97dQKlDXVvxbFMy6AjKYLgrmt0ZMzk/Fnji+G7xXOKf56KnH+c1b76DMutTD6FFMndc8NJlKBuJhfz4gAC9W57i5t0FmHZujBUqB222hNgTrqatcPCE8NE3GaFCjsxVbYCUSG7qDZmvlC6CCwGNjVldvhxOIKCHbyb9mQzGKyCiNkC1n5xXFXrz3uUh46PZBtNSbjbftQBEC7NdDnjh3B6sc85DRxnbQ1Gus8tQ+oxz0kEjD7dkYaxzT2UgewtPSsJz6QSpzfM3mqxx2A9qgOQoFNsg2Z1HDZys5lunYkDaxidthlacNmlnIMSxf+v0A0HgZIHqHL3RFFXVhDvwwadH0L6/+ZdoL1vUvx5nPqXRFjltqGnmb4Km9y5dDMQ8FVWjjy7pN22mD4abbTMY8Dp3Y1k0wSXunL7u9XqSX6b1N8qLjWAWaJmNoG9ptgdr2HACndNKS6st5MphKecyhhA2Op8VAIGoeweXxbe65cSon9fdzqGvyOCj2WkojXaODT4PR1A8YhTppAPUNbWGKa5acETnnyluO/IANvRAIK5qpG3B8e8T8GXkZLmo5hnsMOVqUgmtvRW59I6+5vHEnPSMuMkgqL/fIqIBVXTy+LJ0LLHkzDgFmzHxB5w2HswF1npEZT+c1szZnWhWMbMOsypl60ep6dvdVDJ7PHJ2nPuPIig6X54QsMIh6WmRivtMUCHQcUEERVFhyLTzyYulkMPBeoVqF9xraaIQT9bZUo3GdxkeHRAL4Vu6f85q2ydDGidlOlbFoLE2dkWUykbu3NyZ0ms4ZhuePsdrTVBnjQU3TCd+prnKCF06HRkp6TW1xs4zth+8xt9LQdl7T1PKdM5kTDlRnxDjMWeraMjgzx3tNV1l5qXeGyXhBVohe3N50xLCsxdzLOI6qQnzhVeDmdCIqAS0saksI8MXFKUzmcU6nEpm2Dl9ZUJp8UoswX6cJmad1hixzqYQkyuSKdhLIjtUJmXFvSfDYbK5oe45ENJwKUeCxLyeVEf/QDaDcg8VZRR4UplHoTngZ4S2+8delp3WsYx3rWMcbxts2o1BImlV1Fq08//Tg/TxW3KHULT91+LVk2jHrCnZHfaNVM7StzHbdiDLrEunL4Mm04/TulG8afZ5fPHofhXaRiKYZ6o6SCFtVLpVxericIWAj0cdHmGnfZAeSfHEP0ew1oBpMIgtN9EJgpivmQf1Mvi8PuWCwqmPSb0t5CCaZ5gAMIdlIrpaOHAKZBVLZ65w5TNv3QSf11545vefG/NzdP8XAtIxMw8zl6FhS67Mnqzx50dF1GtcZXKepOiEKfmIqNiNGBQam5SNbn2JiFimbAFFy7YlwpWq51m3zO0eXAfjObTGV+dbNT/OZ6pKUi1ZUYH/m3rP8e7sfRQNG19jQLTWAEPZzTyjso2fU9t7Uq7pOBo/WPjb8M2a+4G474bHiNnrU8dn5Ba4ttsgyR9NlTI8HbE4WzJymyBxNk2G05+s3XlzZ31Jae6QbqmBPZIj9swLSLP3fb36QJ8Z3mXUFt+sxpWnR2jObF+xuHZNrR9WJvtkga9E68M/uvY/OG77v7O8B8PzxGfR2jTaeesPJjLU16EFAWcko3MiDDdLQDiyhl70NrQLX2+cCyqvkRa48ZMYnKKY2nnZho3k50GhUtPB0tSEbRwxoI5bCvpWfs67A3CjoJg7nRXa+6jJ8a/Bx13WE42Zlt/QDB1yjIZNyb79MqyDLgcx2dEEznxd0XtMpg28MqmjpOk2oDF3m8Y3hsBtSjhqmbYnrNPOqwEbLXuckKxoMGjqnqWpLqaBrDMErZl2OcwrvlkALpUFXGl90eK+kWtFqzNgznxXJPhgEfR5UEOLdCnRVKRjcDSye9q/rNdSvq5RkEEoF5ueiGnMDLo+ABaT0pFoxs3qrntnrjGId61jHOtbxhvG2zSj6uc68tZzNDvn120+zc3pGGxr+8OASF4cHnCsOEhms1C2XN+/QBc2p8hirPDvZMXNfsGXmHLYDHt2UZm3tM/abwYnGo0WkQFIjVQXa8KBWk1aBPHg8y1kjkLSUdDRWWTVfuV+6AJa6M6vRz5RFa+lk38Lw4Db6bVt6Mpxj7vu+ScBG7aImLKcZYjsZ0L2+DoHnD8QIvnEGa2Q/8zpnc1Bx63BCbjsalxGQxue8tdxoNnl+/wxnRsfcno0Z2Jbv2o4+HCvn7tHJy6D3ffi9649ycGOD7/6WP0jrLe/D0hbzsF3q+veKo+n69VmL6pKuVL+/Pqu4X2MJiMuld+KC4l474qnSoRTcqDY5akt2R3MK09FODLMm59RkhtGejbJiI69ObNf1WQuif9XrXvVqtSd0sZTnk1cvcv7JQ466guvHm1zeusOl7QNCUNQuk8x3MKMpKraLOWc3phw1A7qg0zmUpuOxs/e4eTShLjwBGJYNY9tg48w8lKJLRi5N0hBWoJcayDy+UFjtUxM19TDi85Mph24UWeapoy8GgF5oVKdovQG31EBStdT6aUQ3qvaGbtOh5yv1fRWgVXTOxP6IlgxlsMwafFCSnQwFPNFnOp2PjfgAjOT3PO8EVu4NoRUZHoJCdbFxrwLlqKGwHbXP5DrPLWEA3mvyzOG96DY5p2nrjFKBbwx4xUEzoJ3l4vOyKdlN6F9OsRHtvIZO/pZZh3d6aXc6X4IKdKNOqMTOHlr+3o1C1Hpa3qOwsrpWARM10nwWTYuM3DMVSCnBCVmPP0a85YFCKfUU8H+uLHoc+G+ALeAvAz1M5b8KIfxy/MzfBP4Sohr210MIvxKXfwT4+4AB/lEI4e+8mWPogsYacae7MxtR7VoRIdMdmsB3bz53QifGj1Uqv4A0ix/O9rjnR/zlc6JXdOCHfNfWc7SbGVNfRl9exR034cCNqLzlPeVVTAhUIWPqBxy4Ieeyw8RR6DV9+kGob5jecRvJvGhiFoxUQxMMn4kM8VVtnP6Y++gHKHHIcw/o5qx+5qSYoLy0ztlDhr7mheYc0EtZix/43IvM+DyKxXgUQ91Q6JZ71Yh5nfPQxhGv7m+LexowLmtuHU6YDCuqNqNdWIpxTTPPactGeCnAa4eb1G1G0xk+Nn88bV9KaRqPiuUsw712xJ/b+hRnJ1NOjWdp/WfKa1yye6k5/Vqzw6lsyn9w5g9SA3/qB4JK0y3PVw8xNhXHruRivofGs2Gq9EJuQ8a9boxDs2VmUmJER2BDyWvNDpW37GQzfNC80pwiBDhoBvzFs3+4cq2X92CVET7zBYduyFl7eELi/Hr0gfZap1LhzBdMo3EUwI9+zT+L5biW+bbcj+FOne5/P4CNdINVXVoH4GPzx3BB8/1nfo+ZL/jbX/gI5YYcVxvNoIal6GIVk5r6qMBEnhFBYTPHoi2hcGjrCWmAkBdZiKqAuo4DQpQzl4shDe+QRWOpNr70O5VQUMrHwcbJRKvzRvZ1JH/v368qGi4ZHdDG4Zsc72XSkgYKJw1iHZvwPooh4lQqk/mgGBQNXdBSFuuUDIoEdK1whZaBbKykPBVkADPW453G60CndHrxd50hNBpXkgak2mXYYUt3r0zlstBpskrhtwRh5sPymIqipa77yRrUQ7mWQS0bzf1goFsITs4rP1C0D6dbLS/8HnuQRwCUF+BMMFCdjgPPfeu7t8jMfssDRQjhC8D7AJRSBvG5/lnE0e5/CiH8vdX1lVLvBL4HeBdwHvg1pVTP+/9fgG8BXgP+QCn18yGEz73VY1vHOtaxjnV85eIrVXr6MPBSCOEV9YD8YYq/APxUCKEGvqiUehF4f/zbiyGElwGi1/ZfAP7IgcLFlDBXjnlV0AZD7TOZqQA798lAezih9XTHaSZajHpOm1nSQ5LGdJ00kwAuZQdcMIf87NFX877y1bhOy1ZWc84cLTeqSJwGWMoeD3WL4TBhqJeQyI5/efcpct2xV40Y2oZh1vBNOy/wL++8E4B7iyGXt+7QeUOmHbfmGxRZR66jd7WtOO4KNIHdYsZhW8bSgKcLmsZl/K2Hf4Gr3Q6/ufdk0uKpnGVsa84Ux2jleW2+xWEzIFOe7XLOI8M9Gi/M1z66ztDU4h3ez7S81+SjBmM85bjm4MYG9UOSRWwPF9w42GBR53zs4GGxjzQd14832SoXaCUWsxt5xQe3XxJYb9BM64LfvHsZHxQfeOQlRpGxvKEr/vH1D/DXL/16ggBb1SV9JYfio/uPcrac8uLRKf7rx3/xROMceF2tJ02LV8Lr+CfX3s+is7x75waTrOIPjy6xuy2KoltmfoK5CyR+y3KBrCcKvrFkZrrX0XqKPIpo8tQ313uYb//31WylBxyMVJMUa3sI8scPngXgWyefxqqOs+Nj6oFcl8J01E58z2uXMSlqrjS75EUbyyWKwnYQICsdmXW4TBrMxgRaE6TEkwVCJppFmfZiudrPpE2QJrZT5EcyS1de4fdy9PmQjHlUzAC6eA2DWspjt5HV7bxGqQ5jAr7W+AjVzZSnCQblFfqehbMx4wkKD6hOSRnIi7mX0aLjhJaGvDECZdW1QFHL6xluS1HmnsZJgzrLO7zTaB1n9jpmMo2BTpPN434CzJqcEBRh6JLhVuhiuSeW3UJ8L6gTpaJ4LZLELycU7pWKjefY+O+Gq38LktUoxFu7kevXboptcNDwjn94lZf/0sMJ9t9uSFZil1Jmf6z4SjWzvwf4Jyu//7BS6lNKqZ9USvXC1heAqyvrvBaXfanl61jHOtaxjn8D4svOKJRSOfCdwN+Mi/4B8KNIyfFHgf8B+KEvdz9xX38F+CsA+ekNOi9NsCoIiUc06RWVy/AoXuuWtd8eInqiBxB00vi/0u7ITC9qvfR+Br33AMCn5pew2nGlPUWpm7Ru5fNke9nrR/VN9GSLqmumbnBieR/XjzaoGsuTp++w6Cwv7Z3im3Ze4PrRBkYHdoczPn37PFtD0Uea5DXP3zrN1njBzmDOx159mNPbU5ouY9aJR0LVZZSZNJaNClxpT4m/RZzJ352PuDg54Op0i8pZThfH/Otb0r8o85aLowOmXYnzmsJK07BpDEoJmenWjS1OnT2i7Qw7ozmt1zSdIY9kosZnHB4NMVrYs02XceVgh41SZsfjvOa4KRjnNbemE3ZOiWrtq+0OE1tRmI4rezvkWceV9tSJ/s3eYhi1rU5qILme4BYUtTe8cmOXly6eZe5zzmWHTKKz/NQNeLk5zbErk+6SC5qZz2lDxo3phEx7XFA8lB/wUH7A+zevYKNPyEjXSbvpqCt5z+g1sbTVogN2q93kbjvm6cH16I0hpMgv1qepvOWZwfUTWk8v1mfRBB4pRBds7gteaU5zo9lkbGqeKm9Q6obK5zw3exSrHV81uJrg3TM/4JXmFB8+9XlAYNcuaL7v/O+nnhhIX2zqxJ/B4Pnx2Z8lMz7pKxntmezOxDQnWgYDdK0RKG1QYAK6EyvhTHkhckW4p3IyZdYO2rHMwoMK6O02QmmXhL7MOJnpeyGDpbq8IkF2dU9KixlLpgXG3sQmuT/dpBkzxP5HEI8HyTAUzqvUw8DJOqnZrAP1KUeZ+ZjhmKV5kO4h1oE27iMEOcd2jPRCnGRAISiU8cumvfVkx4rmIcm8+n1r7ZMOlrzPgmyL2HhWgSyaFoWAdGyNXAO0HFM626j3ZKJJFYBZSL8vmMBL//HD6boFBeU9halF7+mtxFei9PRtwMdDCLcA+p8ASqn/FfjF+Os14NLK5y7GZbzB8hMRQvgJ4CcARpcfCiAP071ujG/EhcvFl70Lir937VuTUFfVWTLt6LyhC5pMeT5y+jPcajc5aw/57YPL3FpMmLeWJzbvcmu+QeMN/+kjvwHA0/lNLue3+JmDZ/mt6ZM8f3SGa4ebfOjSC3z24CGMkgfl9OCYa7NNQlCcGU45akpc0GzmC1453MF5kSM+NxFp6CLrWNQ5WnumbcFRVTIqGg7dgONZSWYdG2XFqfGMRWvZGcxpnGE0qNmfiozDuZ0jrl7foRg1XJgc8urhFs5rphRRusHz4698iO946NMs2oxTAykb7NdDuuhe5lHsTGYczgecGR+zZefcqjdovWY2L7Cbh7TzHDtsyHPHM++4SuWyJPG9VS5oIpZ8s6gYmJanLtxKEs79l8gax6KzbORVKjdsDReMMjnnV+sdhlnLraMJj+7s0TrD//bqBxnahkVnGWQtW+WCT8we5l+8+jRPnbrNYT2g8YZ3bd3kubsXuTQ5YGBanrx4i1++/R7+6oXfSIZOAFYveG/5anqufHRPs6rj7770EY6jaFvjM4a64Ux2lKQ1eha0VY73Dl/FBZ1KQ1JO0jxe3Oad5TUciqkbCBNbN/ypLyHh8f7hS8vjwFOaltPZEe8sXzvx/Jem5c9MvpA+13NzJlnFuewg8TFyHLkWkEe1gmgrVUuVLX9/aOMIrQKlaamc5aAacHHzMDWGfVBk2lOULa4ThJApHN1E7nOhO4KWlz6ZJyANXpcHDCq9xItSBoreaVIa48LdIQhKpy/brEb/ezDi1pcpl77PyoHJe/el5WChOnmBey+ikj4+22rlZe+9Jp8pWgAj8iaF7dLxeq8SEswHlYyGdOYJLjaNO9lX1VgZDDDp8zoLIgPeW30Hha5lgGhqi4mTKRAhwAUk08XECdEBlwnvRatwktOyWt2PMuNaBdwgDs4ZQEjXFQXNprC7w+pn/xjxlSg9fS8rZSel1Kqu518EPhP///PA9yilCqXUY8Bl4KPAHwCXlVKPxezke+K661jHOtaxjn8D4svKKJRSIwSt9J+sLP67Sqn3IUnclf5vIYTPKqX+KdKk7oC/FkJwcTs/DPwKkmz9ZAjhs3/UvlfnHrfaTWgkm+i8jOw+aDZtxWf3pJzyzM4tPnP3IXYGc64dbjLIW25tbVL7jBvtFi8d7tJ0hoPDEY9M9umC5rguIptadJ980Mx9zqwrmLc55yZTblYbXHnuIuXlQzYGFUqNuL63SfAyQzpclGRGNF4AdkdzDquS5189y9bOTMo6ncYORLK6yDqmVcF+O6StMpzTzJqc3MhsatHZZYPq7oCjYYX3msGkpprnVC6j6bJkV1lXOfl4wbV7m7y6s8PxvERv7uOCYpC13Kwn+KHC9Q3GTvO1u6+kEl4Iiq0NabZOdmZUC8l+3rv1Wiq96Xg3Vjmk95oxX7vzSjJTAk6s13qD1S6VlIa64Vq9xbn8iKFueM/kWtSvirNS1VGvCNXst0O+67FPyfYny+1/+wV5dMam4pFSeDHX2m1GumbLzJPWUw+n7WGmbSiitpYiOMVsXpDrjlI13Gw35fxNlSC4bciYdiVtyDhrDyKfxjPzOXNfSMM8Zhq91tPcR7hr1KhqIZW8QJrso8gKb7zobhl8Wr8Jhj03plRtWmZVR+Xl2I9cyZaZJ65L6/ME1d7QIlo49wVHvsQHzQd3X47H0zD3+etqev3B/iMy4x60sREcaDaljzowLT6P5SITAA+dJhhhdYdommMzJyURtTTSyYyXe2sk03BBST/XC8S268TXPbHBo/ZSL9bXL1uVeU8z+pb0PGdGSj9aSFBkmadrM5l1K1CtQscyUw/y6Gfs3mt01Mgy2qOMwG+9kRKUCpKNoAKhP8742fI2VI8s5fJDFF60eZfOqWe2Kycz/b5K2J9TiLwJrQKrWInEdUkZlxxfIMJjNSfe7LqVctzomkiPv5X4sgaKEMIM2L1v2Q+8wfo/BvzY6yz/ZeCXv5xjWcc61rGOdfzJxNuWmQ2SVfggSqjKKTpvaEOEkwVN6w0Hx1JTXmxajmYlo7xBqcCsypn7nNpnFHTM6xznNeWgofGGeWupO5Ma2f9o788wMJFZHBTX721yZnvKyNbkTxwxm5YM8pZ5mxMCtEc52Rmf7CkPu1KO1RmcVww3KmaLnKqxdK2h1pZuJDOaQd5y7AqoDb7RqF2ZOcxby07W4oOhdYbtT2nCJclcmtoSajHMGeQtB0dDtjZq5ocD1CTQHhUsnKW9PUCfDwJ5HcDWaMG0KTgzmFIYx2hQ8/XjF/id6ZPcXYw5nA0IAc6Np+wMF+wB1SLn60eiZ7SqldSbHGk87Wip57Qaq83n++PlxSmeHcos934I6upn+m2sbktHvav7iYh9BrF6BEa5ZJzUS5L/X3eeJYt9pnE05fnQ5ueT0i2QtiPH1qbeRA9PBciVY8vuL49P6cQaN7pK16r/jFaeLSMw7l7aHdXRBJNsWQ0hbWPLzLGqw+JoMVhIhM4eZtuTLKtgk11tv+0tPU/nfi47TFDbWTjJxOrP9YXZGYZljV3RJ6rzjFODGYVuRTMKMLnH9yzsLAhxTXvIpMaeaZcsO3s9KR9iLyATWKeOcE8UCZIKMmPWQKY8hV6aRYVIqusbz4k53mcEQZFn0nvwShGslya5cWJBGvsmqRfSZyQ64DpNUEt4bIoQJ/JB+iRtk8Weg7yPlAoEH4/BS7YSgsIXwnA3xtG2WToH00S9rUzIiavH4HP5rCYkbae+dyQZBRBUghf7Qq6jzwRw0KvL9hne7MJb71G8rQeKvulW+0xkkFGp9FS7TDgECysPHoF2YWk3ZSA53h9Q+yy6X8l2ZpWlKFo6b7DaU9eWW+0mRnkOmiHX2pyHx/toApuTBYs2Y97lGOMJs4zFxLJZVvJAHEuTOLMiINc0Bmuj3LIz1LXFd5p8XBPmGSGPImRB0TopoQnTdXm+NiJRWmdQwOHlwGb/wGUOt1KW6mqT5BKUCui5kfM6syDTUgob25rStJRGJNIvjg9ohvJtboPh8uYdzgyn5Npxqjjmrh2zU85ofPYA2qhHfd0fq8s8+sSL/cS9RHNjsZlE/fTKQNELN656VvfL+7EobVed3K4L5oFBJ312JTqvGdmGhzf2aaJUhlXuwf2t/N8HfeI8jPLSYL5vUEs/FQ+s31+/E8dGSP/uv1Yan5ry/bqrP+8/x9ddHpdVUf5FK48JJ709+mPbsgsu79yl97zOlJSMTuUzLhQHqIFjlDcc5wXeK9qwLAu3zqCyZVM8FNFRLheva4joHisv5Mw4mcDk8kK3Jr6ArQw8hRb3SR0HEyL/40QTXLFEV8mvwvcICj3oqGtLWbZSyglS5vKxTNwFAV1o7emC4QFKWBCOiCsjd6FVhDgYoJcy7cErlAuorEc4kpzqVo9XqUC9vXyhE0jcjXTwyIDri5AGRNU3rL0Mks5K2bN/z4Us4KPEhw+CqMoW4nLXbD7wOLypWIsCrmMd61jHOt4w3tYZRR9txD+7iJ32QQnWGgi1/M2jCJXMxLUK6LKjWWFxt07KNm0jHAytAtY6KQEBi84ya3JaL5Lhi8YyLmtql8nAbwJ1nQkU1CvyfZ0w2z3/oI8omUNotKTnepneGhWwRkyX8AqMx3nJglpnYKXh5ba6lGEEL0JnIQh23NzNCacVeNHMMZVilNVsjhdoAuOy5gfO/u4JLkgfd7oNvnHyhXhtsxMllnko4nF69roxTTDkyiXtqlnIqXyexAqt6lIjtm8gn8mmSdivVC03uy1K1fJD53+bNmTYqJm158YMdU1Jm7SRhBdgksbTsqFrOeo22dCVaCVF+e49N6byVjS3dJvO91q7vSzZmDn//tmlAGEfvYjfvW6csoRhZEy3IeNON0GrwEaUiM9x0rSmEPc+s0iS4k0wHLgRAFtmJs3sqIc19SUHbsh5u59Mo3rnRatcYmn3nJ/rbpvzdl8ypaj/dLubUOpWzJ9WMp/bbgIs2d1VsNzsNlMz3Khlue5OJ77XPd9koiu+bfuTuCAGT/NQnPCNPvBDBpOKjaJiPrR0TjONGkkg0O8ewpopD4X8X1vhqHReo61P+ZLVnrnXaOuojwuyXZFE72fco6zGKjEpUh5Gg+bE7Lyfuacmb2RFd14zyFqG45rSSplvnhHLRyrJfvvIw+i310fP5wgyacdUinYjQCvfYTXgxHEoHWg3FCGK/4Wg0FH+vOvMCmekJ4gIRyXkIUFxlZLSU9+wDzrIuyKel+qAQcAYT2t7WKxkh73eVuihti34POBKtfbMXsc61rGOdfzJxNs2o1gtH/oQZYMj0S4EReMzMuVQrU4jq2qWRCJtAq03qa8RApjMU90b0J3TsdEm/Q+tAtO6oG6l75ErT5511G2WCEB0Cmuj3ouWEd0HUc4MQFEs8W0hRBOYTgCjKo9qlb0uDKKMaypFNw44r8iXhPJk1qILYbdm2tPoIPoz/ToT6YfoaBYTgAvFAWdGx3gUZ4fH7OpZYqz3JC5DYMvMRNkWsXntjZa08uReZoWlajGxGSqaS5o8ypZPsipZwS5Vb7s02+3Xc0EzUg0Xsn2Gke3cxmwgx2HtPiPVpNp5jovblm3Oo+f3SDVMsioZQ/V2rqVqOR+buS0Rbqo8Q1Vzwe4zVDXzUJBHH+0+VnsHRnnOZYcPNOxz5Sjz5kQPwCFw21VtpqT1tKJH1S8v43M50Qu2zJyhqqNpVL1stq9K3ceGdWXsUi2pEQAAIABJREFUieMt9YLStkn7KsmN65atuJ1+nxNVYW0nfu0ntu2wcbZdqi4pJ+fa0RDviXcJ8guSnVzaPmCc1ZwfBxpvaLqMLqq/LlpLUbacm0zRypMVjkWdkxct47whBEU5aGhNRt1mDPOWYdFQNxl2XEtGor2wwbVnI6uYmIprxRY+D5ydTDmoBssGcGyMu3zZB3Bec9RmvLK3y+WLtxN0+IWhgDXN8ZIMKsxueX9o45P0er9tlCQr3TAaNnUsX0QrfXRtAt1ALFFV3K5ZnGx49NmEt/L9DyAaVelcAsEKKz1TnpBL1qG1x6rAIu81t2S9vgdklQMbCGH5XKKEHOgzTpgj/XHibTtQrLboHDrR1X2QF27nRdRLV3KH+8Gkf2n2tP6+lJTo96VLDeEQVJLL9kFYmJ3X5JpUDmpiycrMDMb4pEdvou679woTsdg+4rR7qQHVCXM0rDwgIA9n5/VSsjn+qV+nH8SUlmVdf7xaSmxGB1TpBFutSIPZY8VtHjt/O8mKPFc9yrnskF1znBzdbnabvLw4zTdvfg6LNHOPgmbPjXm5PsO7B1cZ6ZoDP+Rau82eG2GV4/H8duIAXG13+dj0Mb5h43lKLZ7cUz/gWrvNy4vTfNPG59OL7siXXGlPc7ed8N7hK0kyxSjPxxePYgi8s7wmA4m3XO+2kzz6ueyQka65Fyx3ug0+O7/An568kFjUVbC80pxm6koeKe6mF/jUD/jM4iIexRPFLWHnxkHmleYUrc94R5T2mDqRx7jVbrCTzXgkv5sGtU/NH6YNhq8aXk38ispbXqzPMnUlzwyup/PsJTzaYJJsyKqEB8DD+V22zJwjX3Kr3eJuN2ZsKi7ZPbbMnJkvuNrusN+N+KqByKNN9IIjX3K93WbuCx4vbifv9cpbrjSnMXgeze+mgeSl5iy1twx1zaP5nVQyfKE+RxUsE11xzh6gg6fyNknTP5rfESc6JSW2f37wVfzQxd9m6gZMjEiP/MPqG5O3xM5gjguK773wUX7r4EnGoyrJfSxay6nBjGHR0mWOqrHsHQ8p85bRoCYEJXYBKqByESYc6oZT2ZTvOPVJPhou8x+e/31+/KUPLT2mA1H8D1BLXs/fePJX03vCBZE4/+/ax8Apup0OS1+6WkEcRVlwrSKHIpaUgpbCcTCwccUzf0KkOYTJrVLZS7fiHd4PCN3YM1CBLFtKoyhgeDPQPO1xAfDieTEqGo4raer7WoRAsZ6uMXQuMsAjd8V7BbmXSbEVxQWVu8RW75nZIRNmtj9pcfOmY116Wsc61rGOdbxhvG0zigcilnr8yqzbI2YqfVqou5PpX9/49hHg7ZwiK7rliK9CanYDNHWWWN+9kFoXG1Zu5GLzWuBy3WiJE9cr0DmtVhywnMxa1NygBm3y4gakHGaATidDFL+aRkHCrWvtE0QvracFU00W01IrEt2nzTR9/kl7m1mwlKpDB9E62jXHPF1cP1GKAmH2Pp7fTp+d+pL3lFdjqUhKFgd+wJaeM8xrnt69QRVsKjWh4V3FnK8prwAwC7mUrwi8r3wFyv4cNU4pStXxgeFLqfTkgxb9ouIahsAs5KnUZIF3Fte4nN9Mx+xQjKjZHRxHoUCdZMZR8N7hq6kx22s9eTRfPZDj6yGrVi94d3mV9w5OwnNz5fiG8fPpelTB0gTDmWzKmWx5jZfS5g3PDkWqvC8P3a/1NPWDVAbbLY/TNma+iE130YyigJFa+m+PdM2ZeF+PYsloFnJGquE95VKY2QfNll6ke7BaetpSC7528MW0bn/NR6Zhd/BSWtZvZ2Qa/qPd38EqxyyTezn3BRfGh+k7k5uOC+NDHs9v81HzOA9tHFGalsZnbNiKo7ZkZzBPTVpYlmQkcxd/emNlRm91x0jXPGrvEmzgifg8GuMxKmDijL8b+5SFG+3Tc9uLShpEF0ksGWPDPELTiU3j9j54rO6bz528T0yl2HsG0OIQqCKL3EYdK1cGdO6W1QEb0nZ6moVWgXYUKw5KSktl3rJoLMOioSpyXCPXwZQOkzkKK1nWXIMedKIdVThK05EVHVY5sqKLtO4IkKkU7Uikyd1bFAVcZxTrWMc61rGON4x/KzKKHtbmUakumewR3XKd3i8202L/uAqndVH+V/caNEQZ4NAbqSjyoktQwn77vveRNktdGlkh/og/3YpPbggROucjeWbo5O+c7L0EJQ34PhsxvSZN1I0KlYHxcj+JiRkUITYUgw5Y4/CFzB4P/FJ63SqXmpa95PrcF8x8wQW7Hy1CZSY59QM0Ipcu+kwZd9yEyuepUeuCpsJy202S9pFVHRNdUQXLgRtRqiWjWTIDI9LsiGlQX/92WnO13WWk67TcB81RnBIduCG72XFiKM+6Ihn+WJxYicZzaaO16KoVaq//NNFV0npqg6EJojEk59lR+TxpQAEr2lBilduEjC0zE1iv6sTa1JcPwGMrb5Pl6UjX0TZ3CY8VhnvAhpO6U0aF5LfuguZmt0UbDJfsPdmn6aj8gJlfwpZL4v3EcNCNMPjE6J76klnIU6N+oitypGHdqxAY5RmpJp7/cv3ePKpffs+NKXVs6Gt5Tr5h58X0HelhunNf8Eh5j4vFfjqP/jvmgk7WvfcTIz8/O8t8XlCWLXUluHCH5sAPQQk818T+QIKamn7WHwEs8VmBFR91ROFWdZqgBLJaRvVYpSSjcE78tiXbWcJcfS5Q824YsEcP0pyVEuq2z8G3OmYaevk+iN/P/nh1J0AX78VytbAdVnuu392iHDTokWdgWspBwyBvMdpz72BMMIHBsElZT2E6ykFDqVsG5clGhMsDysfG+Ukvtzcd64xiHetYxzrW8Ybxb0VGASQdmb5P0QWNCV6QRbE+GDRxxrA0AOkRUtbKrMY5nVQkgVRv7ZygmvoMxOhA62Q2Ys0SZSBkmuXIHSJ6QuK+GUjPtylFUbLPJkwvJ1AKvLc/nrrN8KVYQqqgKG5Y1GlR2tQ6QO7pvNg/2tuW7KKHXGajofDc6Tb4rYMnaYPGqMDl4W0+Nb3AwLR876l/JfVxc8y57DDNBg0eCzglx9D3FUyEXbaqSbX2fsZ+IdvHxTlIrzskGkPVCVMn+btKGkU9bLaHkT5q75y4XEbJzNjg2TUna/gTI9te9V8AIbf1vYVeCsOoIAieOKsGscgtdctELZj5IiGEHIqJXjwg+WHijDt5SKzAVbeMnM+q9EapPHlEv/XLy5jiWtUx9wUTs8DipO9AfQLqWgWLxvOwvZe20Ut0GNVSmqVHhYmZH8CuftD7chVG29+LEs8ZM03L+59GLTOx5T2T5eeygxPw4Fw5vi72M1ZjFnKeHb68nM3f9z0whJjJ+RPLvrg4xWRUMSwaDgLMXcGBHvJ8dQ5yzz++9fUA6fsl2lIRGhrfAwH4mb1nKXTH3VrS70w7QhYRTF5hbSck1djYcF7jFhnky/PWvfyGk6xCtxG5qAW6qyIyql8XD6Zwy17JXMi1dZslHSulAu0IdgZL2HQbv+tPnBMTM6M9henYGc0jTD/n8bN3ef7eRbZHC4qso3WGXHfsjuYUuuXUeHnP92ZD6VFsRkjvit3qHyfe9gPFUhclJGnhwHLAUB6BhQWFaVZf5n3jV5ytnNMRukZarhA+Q8I8+2WzvP+9aw2qDFHLZXlcbrBkahK5FclbOIiUdb96FgcpHxRWe9roBa5Khxp20oxG0lITWeHDoqG+0JDFBljrDLoUKfI86+jO15RZixl0jG2NHnTcajf53P5ZyvhwbdoFr023ZCA6tSrY9+aeJvdHJKQ+aGn88aCrX9rGSunhjWK18QqkUg88qNv0ZuL1JLXf7Gfe7P5WB6cvJYR4//bNqm7RWwi/MvjB8qV8P9/jdfffl4O+xN9X11t96d+vJ/W6+ww9bvW+bX2p5SgK3fGeM9fFZW7DUPuMFxZnOWOnqMzzxaMdnNd0nU4NcZ07vBKghw9iEvbi0WnRd2tyxnnDtC6El5B7slKeocJ2NJ3BtyZtp6ktDCsy4+S+9OznVuGKgG6ksa0ggVYSM3sUoDEr5ktSOlYRrp6Wa3hqawkSWTWNkga6J9cdT23dxgdFYToWzvKFLPDM9q1kXmVU4JmtW5y3B7xr60ba3m/NniBYmccGA91b5FGsS0/rWMc61rGON4y3dUahVUjEt36CuEqWCzGjWLENFnLcChyvX7/MW2bzQtQY4zb7kb3PUurKLmG3fZbRK1Vmy9nTqk6MigYjohWjl/BYHVIlKsscXWcojKPqMkZ5Q6Y95ahB60BhO4a25VZVwACGRUPnDIOtivlRyVwHhuOa4aim85qmy5hsLBhmDaNhTaY9w5HoJ7kIO6w6ufW3D8ac3zniwA8TSe2a2+aC3U+lFYdKUttVsKmxfNtNKFXL7TDhjJmm2c09N5amqmqxdEJ+CpojXybtqFUiWuVEk+lRe1dUY1muD6T125ClxipwQtdoGre9WgLSeA7cCIdKsNOeEX613WWiF6k5DQJlnfkiscp7napeo0qOpQE6pn7AgRsy9zlns0N5hiLhrvdeH+k6aVQ1wZwwLipVm/S1euMiG5njbciovE2NdYNnYhZU0RTJxcb/qtZT38yeRN0p4jXs5cP75rRDM43X1RBE8yk2s/vl/frEpv39zew+i6iCTcz4VaBAv09DYKIXiaHfq+32Df7fnj3Jk+WNtM0NXYlEPYbK5/z57U+cyFh6HayX6zNkeUfVWCZljbVi/brwGmMdSoObi6JC0xmMzjg7nHJ7OqZzhrvXNlGlQ1uPzTvaNmOOlK4GL+UMH9qnc5q6ypN3OiRVb9Fgipaoq9alIFlD8NJMzwqBsnqv8EOHD6KIu8wWAtkcvu/U7/FG8UuH731gnd8wT59Y9tN7X8v37/4uR77k+3d/Ny3/7euPo2sIG4FgFLzFhPXLziiUUleUUp9WSn1CKfWxuGxHKfWrSqkX4s/tuFwppf5npdSLSqlPKaW+emU7PxjXf0Ep9YNf7nGtYx3rWMc6vjLxlcooPhRCuLvy+48Avx5C+DtKqR+Jv/+XwLchXtmXgQ8A/wD4gFJqB/hvgWeRMe85pdTPhxD232inUhuMtb4sRPmOVbMblQxGYPnTRngsxJlrXTIsGha1ZVC0acTvCXdaeTFpny79HvrmlvyfaAW5VJrssxilAsYsh/HeDpRW6vchKM5MpviguDMd847du9xdjDhYlDy0dQRIc21aFzw0maJVYLOomDYFO9tz/LbCapfUZYtMCIOnRw2l6biweci58oiDzQFzl3NuLPvaHcxFeuPMParOUnnLrj1mg4pdc5y0nvLYr9jSixOEK5TjXHZIGdVHe0tTlON0dpSWL2+WSw1XWNaxN3TFUNfpZ2p2K1EvPeGREGfA/TH0GUyuXGqUr64/0jUjXd9HuNNY1Satp/+vvXcPkiQ5D/t+mfXo6u7p2Z6Znd293du7wwEHHA/EiwQJAiJFEqQokGaIlikryHA4GAZpKEKkLTpkOwTRVshS0BYjFBQZIYUjIBE2ScukbImUEDRAEiApU3ZYJAC+8DgAd7e3d3t7O/uY2Znp6Z7qqspM/5GPqurpmdt7gHu7rC9iYrqzs7Iy65n5PX6fvU4s68pyluzM2K9aMlkyEPOGW2dt1D/nVhLNMTVZT3714t2E/Yzci59Ze66Tt2kkQjGKa0aTN64jYcNxt+y1ZsefyHlwCGjOwKUsGbHAl6Ji6PgyLdYTKpT7utpIMpkzon0eJjpj5Mq9lCGwsC6fmtSOReYMRdGya+Qm5lNbj/Pn3/Qlm2uE+t7NRNlIwtQ2gCsklzhDltn7tBdXjPpzIqlZSedkWUZVaQogkSo4gkzLHpG09r3Vswcc5glxrIljxbBX0IsUszKheOuMldSu2LO0tDF5UpNEChlplMDaKoSg6lutQBorlJYO+WGfCya1brGx1BTzBJG6IECpUQ77IzFUA1o8ruPkSJ1Yt8qk0IykRbGMRJsrp/rWfdlIQojAy5Wvlurp+4Bvc59/Hvi32BfF9wG/YCyx6t8LIcZCiAdc3U8aY3YAhBCfBD4A/NJJO/Hcpgh9ZG1kvX904JxoI1Gpveh6cRWWihrBejbl2dsbPLC2jxQmqGX8716vlYxrIFpYcjaSjjTFRO2CJqNLa2G9M1zsxQcv/r+tuv7G8aKMVZ2oxoPsJGneXB7D/S0jG0X89cPLrbpvG1wJcQO7ahhYT+8bPR185BWCK8UGO9UK7xg8x0jmlCbiqfk5Etevh5JtMlGGvM5fzh/gHYPnkeiA/r5SbvBCsc67BpeDZ9PUpDyTn2FHDXlb9oJ9WWir0rhcbLKnBrypt8U4mrVYTwcq4029rdD2TbXKi+WYx3rX7UPZRS5fLk5zqxrx5uxaeIBPdZ9LxSYHKuPN2RYjeUhpLGDw2fkZx2Oy9XeqFctXKoesRHMeTLcZStv2i+WY2+WQN/e3QjzFrhrwZH6evarP4/1rjKMZM21jRZ6bn0YjAuupaLCeJIZHezcCR+rFco3b1TCwnlKhyHXKl4vzzHTK12QvkojKqbBq1pM/JmBjN54pzhChA4trYiz/aaZ7R1hPzfKLyTaZLNlXGZeKMygkb0xvhOtvWw25XG4C8Mb0enBI2FcZX56fZyAteDGSmh21wpeqVWY6ZSCLUP+vP/I7fDG/gBSGVFRsxvvcrFYbL1cVYkm8+ic3KaWJWM2smnVWJoyzQ2vUNjKUl72CUkfEUrMzGfKGCzscVgn94ZS5iq2B2sUYHRYJt26PSHsla6szelEVMmH6XPeJdxeKjc18p6khbFje0+Gsh+qVJGlF1YuIYuWSLBlEpOnFFYWKiGRVgyczeMYdx3C/LzgIaCOO1JGJbpVpI3mmtKDDSwuefzq1z0ATG0wjqdPLkdfCmG2A3xRCfFYI8SFXdtYY403vW8BZ9/kCcKWx7Quu7LjylgghPiSE+IwQ4jPV3uw16HonnXTSSScvJa/FiuKbjTFXhRBngE8KIb7U/NEYY0QrV+ErF2PMR4CPAAwee8BIN9OQwoQZfB3x6SKnYxDOz1oqW9e/zb0rohSGd5+7wqTqITE8N1mzv0sTjNc2164OEdl+W0+GlfsxZuyYMM5QLYWxkd7abq+1DHEWzCVIawQ7Ei+w4AralDt1JW1+ToQmN9HSurmJUS5RDhBYT17NYvMzw+O9a4z6tQoiRQUuUoo3qloc9Tia8Wh6I6iCPNforb2rvLV31Z4f186GKNnMJqGvpYlI3Pr4ndnzgFV1pKgW68ljxjNRhmjvx9ItShO10OZvy64cYT1l0ZR3ZPWy3auegJCzG6z6KZMlb+ldI8qs6slHU29EBzaWw9l/p7oXVEvjaBZUVZksKFWfgZzztf0XwkrCG/uhZj011Vqe9dTiMUUVG/06fsSrnoZOdbeIGR/IOZv9mjtl0eZVOK6LrCdf7uvWrKdnW+fMb2udDLwR2x7bYVTwvsFTrXbWowMuxjvOAB67VajgjclNHklukaIpkMx0j5+/9Ta2pqs8NLpNPyp58vZZzg33OZMdIDGsxof0ZMX5lT1ylRALxak0RxlBPyq5XQwolE0+dlglvGn9FrHQ7MwHnF/Zo9KSNalZ7aXuWrCpVePTmoOyFxwBzgwKtBFMiszd/6KmH7jnjU6t27uP2lY7PdL1fVQqKHsxsVtRZFlJUUTBgB1JHYjO6R784rX32mRpGNLIGsC38yHDuEAKzYODXX7x2nuJpXV/9ymWf/Haeyl0RCoVZ/v7/MLW+/jOjSf57Z3Hg0u/VYPbmBEdQXK3EhcZY666/zeAXwW+EbjuVEq4/95R+CpwsbH5g67suPJOOumkk07usryqFYUQYghIY8zEff4u4O8BHwN+CPgH7v+/cZt8DPgxIcQvY43Ze8aYa0KI3wD+R+8d5dr58Evv3741E6GCMdm7swZjszAop7LTkTUgSTerl9gVw3ef/nwrovfS3nuIItVi1GstbXKhxqxKKRvRLYRBZzq0aYxAZ27FEWmqMrLGczejMAZEX2HmkijSll3j23T62cWAMF+WNlYUPkCu+X9RvK43d9Z1347/7/lIPtnPRPeZqIxzyR4SHWbhE923jCJhXT49d8nPgj2PqTQRU2VZRV5XPnCpTSe6T2GiMPsFKLEsnsJEbEQHNtWl093v6oELyKuQkSV6el6Sn61LYcu3lY269bN6by+Z6P4R1tNM99hVg8BjsobsBGVq19GRzMlkQa5trgs/Uz8VTclk2WI6+VWCPU42rWmECSlF/T53XH6JVXloXWndisuPyfelND2mOg3ndDXKg+uyd5sdRzNSoZDOldenN/VOAQClTpk4ttdYWtbTzMTs6yy0PY5mLdZT2KdzPc51Eq7PkTwM0dzaSK5Wa4zkIauOl6WQTN0+fRs+6nxC5o5vnwvx7dCXXT2oI9VFyfvXv0S5FoeZ/TtHz9vEt8JwqxxxKp4xlHNOJxNmOnWsLmsnO1AZvZWSubNx+d+82GvQGuK9q3LPuS9rY1fVNZHArrZ++bl3c6qXM0pzjJb2OeMSk5nEIIE0UuwVfYYXJqwkBUpLsr5dFQ+Sgl6SIqVmWiSkseIg77HRt6rz4hQ8t2sfe3GkKaqIM6MDEqm4sn+KSBrO9Sc8vzdmNZuzM+uzuTJlkBU8vzcOics2elOe31/j+uopnt9fa3HldM9SpJFQjl6ZcufVqp7OAr8qbEhyDPzvxphfF0J8Gvg/hBA/DDwH/FVX/+PA9wBPAzPgPwMwxuwIIf4+4BMX/z1v2D5JrBrJ4X+T5dGyOqm9nbz2xXsm+eXZN/QvU7qbVhvJz1Xvo5/4C0iEh3u514Mzto0kUsSxTQ4khUH06wsykhoTa/vfCKLYRmJWpYvx0BImMQzsS+afXv1WpNCsJHNmVWoxwlVKKu2DLZaa2/MBa70Zp5Kc20WfQVyQqySMoVDWcDeK55RGUumI64cjzvYnPDLY5tLsNKN4zqFKyJX1MX/f2jNB3aDQpMJiM8o4Dg9gIKh3gNpQimQjsghv7xmlEFalEpVHEB6R0M6HfBHhodmM9t3n2kcfoVrlvo2m51SoLzQPxTsUtNVrmbA++aOFSPNIGDbj/VZZirJ4c9nOWjeKDhlFh0vxE9bLy6qAMhfTMJBz1l0iKP9iSkTFgDnjaBbQG8pIEnd+h3LewomkYt7KkucfpAMxJ4mqAOar+6l4JLFOhx7hYdtpezLZsbdxH+FYOYTHERGKc9He0QhsoXgkubmg5lRL9zmWM+uNE+WcYy94N0WiZDPaD3BKj0X3L6PFaPKyF7mxqwXVYxU8qRKhLGTSSBevUiciUwimJmVVzJm6ieHiPhbP8++uPGY9DRPn4RVrhIdvapsJTwrD2fGEXlxZg3lSksUVSaSYq5j1wWHI2703zxhl83AOypGmnNiXedYvGGZW5XVQ9DiYZUhpmKuYvX37sl7N5khhWB/OuHJrzPn1fa7eGnO4kbB30GeuY/amfaR79mRpiUk1JBqd1vFmL1de1YvCGHMJeMeS8m3gO5aUG+BHj2nro8BHX01/Oumkk046ee3lno7MTqSiVFatEKU+GrVOXOR9qPXCKL3B2bu8aSNaM0VjBLFbKVgVkE0MJIdtfG9VWV9rbQTCrRoiqW0qyFSHpEI+/WM+s5GeUazQawXCGbgv3V4PxvHTK1N6UcX24YB5GYdZwdnBAZ+7dp43bt7i1mwY9nNYJBhg3M+Z5D16SUWpJFlSkUaKL+9sMk4Peeb2ad577lme3j/Nft5DCviWtaePzBSVi8T2Uw9lJErIgGhuQuNwhl21hNUTYihE7e7rjdvNSU3Tf36RgVy7COvGTK+5db3fgugI3trmULccnJpjRRgXNPJjN7DXi+whmya1jnPwK4LQF9PepxZ1QqW6p9K1TXCl9n3QjXYW+2OlVi/a8ahWP1vOD42VyaLxuT6udV1/vBZjUJrb+bzqzeNty21Zc/+Ln5vHsJk4qO6LJDLGOgk0Yi1KE6EbK4sIQ449D83j7aU0kVvF1atHbexRW7zGC2qnhEiUYfyliVE+0Zbr5+Oj65Qm4sn9c8SJTU4W8nH3rGoZ4O3rL4Z29MJxjIWiMhF9WTDXNpnXVr5q+zhUiNsp8ekcIWCQlPSiilhoVBURZwVzHaMnCeJUvbJ+y+otXrx9iiRSVIcxuYqpiogD1aPIY6LYPn+GWYEcVAhp0HGMHr0yKmDHeuqkk0466eREuadXFGmkOChssvc4sbNRv6KoVEQUVy2dnMeMx41Zx1zF/NvZW5ipXtAZ91wSk9RxWRKXbD3pVaH9VCqkNAEd7cmxUhj6aUneS+hFFYNeiTbUUdw49kspSfoleZ4gsPrJM6MD5lWMxDJq8iKhLGJ2d4ZsvGGG1oIsKpnOUzaGMw6LhNnMGuWGvYLdWyu85Q3XuD4ZMcl7jPs5t2+vcHA65eCwx6FKubG/wqg/5/ZkQG5iN5OrXECfDswkj87OTWKRyQ3ctUeNe9ZP5Mr8jMobKG09EVhPU5NSmpiBmLeM8p4l5A2oCmpmknfflLMWRwgsj8jv07eRCoU0lifkDcw+lWjqdNveqArW/uJtCRrJ1CU7OhPvhwRFnqPk60MVZqTKCEoSRiJ37CXDvsrCCtGP07OeJJpMlqFcGRlYT0NZoNGUrn5pYiK05TGJuswjybUz9OcmCc4YAzFvrW5CuZyHlZ035Ia+GLsimy2MMxFVKPdMJ+DoPl3b/vpYtk8gGLkzWYbyic5I3AzekwB8WlmfhMkbGT2DKySoatgm/DWXGNtGIWxa2MIZq5sMsInOwvWcCGUx542VXiIU0q1Cvn/8GWsPOdXjv7j9A/a4OdfWUkbEsWKcHfJX1j8d7EPNVbJ101bhu7+mfmn7PZYqMJ5THKSWyRbZ6PJYaLTTPKwOcgod0duwjhFe0/FXN36P37/xkKUypIpZlQbbiS4iRGSZU0oLBsM5Qhgmk4Rs9ZX5x97TL4osKlmLbukLAAAgAElEQVTt5ZyOJ/R7DRicMCiX30EnNqZBI6yXQsO/eBjNGcYFn9j6Wt65/gLP7m9QacmpXs7ZwT7PT9bDi6E4TEj7pVUrOfF+0gKC8UgKw/40s1m5VBxyahsjGI5y0qhCVRGD1Zwospm0ZjeGFJFmXsUkkWKYzKn6MmTdGiQllZY8cnqHLKoQwjBICibzlJVh7kCAETJ1SIhszsE8tZCzocsmF2kSqXhwvMfN6ZBiv8etcsRocNgySPsc1VPdIxXWOClFO9+CxRqXAbnhl/se4bEeHYT2gjgon5emesJ76fg4Cik0WkgGDuMw072QA2Eg2xe6x4n4vjTVJ4moXF6HOo5CYh8ETaN403NsFNf5KGwcyZxBdBTh4XNGgENsuNiPzEW5+zF69dJQVi2onh+vRZXUCI/CxaKM5FF1nn2h1RiQJsJjRO1hdRLCo4nquBOERyJKhlHROq5NtIeXZQgP347HhgS4n48XoSKLyhBH4WUk8paqSAqbaTIVJUN3DTWPYSI0A1kGFXKEIUExjnMSbA4ZOx5BKuaBymDHbX/voRhGdsIgMWGbzEWHp+58ZGlJHFk18zyKeWB1n1TaLI4RNUhUidqAnqLD90RoSlPRc5PSh07fZj6OGSQWBDqIC7bzIQAPrO1zun/AlcmYC+t7KC1JIsV6b8aqmHNuZcJKPOeBzT12DgdkWcmkygL6HGE9qc6s2NibL+8MeWj9NnWm9zuXTvXUSSeddNLJiXLPrygOyh6b8T7jQSPS1gjiSIfVgFAuvqFhY5LC8IFTf8IHThFiCP7civ3sZ4c/tf/dIVNWNiyYH9bmyX5ccnB7wLnVCQdF6qK2IZUV59f3KFTEmcGEnVmfWBgqLUlju0I4s7FvMeGJzYF73Qh6SUUvrphXMdOyd4T/lAibr/tf33oXZRmzmubsJ1mI8EwiO4M/KKz6YG1wyKn0ELUi2ZkPGQ8O2S36VvUWac49uMO06vGl+XkSUXEu3qMkYrta4QuHD/LelaeBuTOgCr5UnmdP9XkiuxpWBlvl2OaC1hmP9661WE+X5md4on81cJc86+lWNeJrsqsN1pMt31MDnsiuBtZTbhKeyc8w0RmPpjeQkfXp36pOkZsUbQSPpLfCPq+UG+yo4RHW0/PlBrfKEW/JrpHJIkRXP1ecZqIy3pRdD6yn3CS8UKwjheZh13ZperxYrnGrWqEnKh5Mty13yiS8UGywUw15U3Y9qEMmOuFKuc5eNeBr+i+GYzXRlvVUmog39G6wGuVMXbzIpbn1uX60d4NMluzqAdfLMTvVkFGU83B6i6GcM9U9LhWblDrmLdm1FuvpuWITheCx3lZQEeXasq6kMLwxvR5UiVfKjRBJfjHZbrGe/DjOx7dtrIfKuFxuUpoosJ4Sodh35XCU9fRUcY5MlDyS3iQTJROT8ExxlrlOOBVNQz72Xd3jUnEmsJ4uOl6YL89kySPJreAKvGtS/vjwYU5Fs9AXrwL8XH6Rs8kuZ6IJmSiZmpQr5Qa5TtiMJ1yILV80Nwmfyy+GeBgfGT41CX+UP8xGdBBcjROhmOmErxRnSYVNBXB6PLXqHwxFGvHXL/5OUJHu6j7PFGdJRcU4mgX37onJ+GL+IBfT7QA8/L61P7Aqr3F0JCtjU4aO/bXo+LBvevzI+d+118WZHj/97HdZbURUEPUUcaJQSpDFFT/+0KcA+LGtH+S/eviTfOrYvR0v3Yqik0466aSTE+UeXlEIetLyf1KhuLhyG21kMBr75EQmtcFyGmHTGHpGk9Q8Eu85RpEMOkxrfLIuef3Y2hkGcUGWluSzlF5UG7Q3z+7VqxanDwRr6D47mHA7H/DE5nW0EeQuPHyjN6XQ1mCdxSWx0AyTwvJmhGIwKBnGdqbnDYTg8goTcbF/m+qcpB+VnBta2q13Ax6uFqymh9zKVzjbn1DqiIdGt1lPp9xKVrjQ36XQEWf6ExtZXfX41evvYq5i/puHf51MlPz69tv44XO/G2wVXle8mU2CTtsHRz2WboW+AUtZT16P7llPMmu7Ymai5G3ZldBOaaKgW990AWBeX25ZT7NWUJRv27exyHp6a+8F6NWrxkQohnLOaAnrKTL6COtpKOeM5CFPONbTRPeD7eZr3T79LE9hnQ18zmxfBpBRsDE4aJUv40tpJAMxP5b19A39g+BQ0GQ9bfQP2gGLHM96GvdeaJ03hWBDzBgfx3qKpq2xLJb74w44NtQzrXYyUfH12eXW/hSCjWjKRv/Z1hh9+Zn+pVZKUG1sO+8fPtk+rqIiE4pvHX7Z9UO6yPyKzWxKJhSlm42XRpKJivcMnmYo2vaIdZHzbYOvhDQA3kYxkiVfn12hNJL5NOXig7dJhCaWikLHPJLsWIcXoUnljHP9Z0hEnexobiKGouRbBl+hJxSp0BRGcop5cHiYLfrvQxjzQFbkJgrPmaasxvPw+0OjHQod8/xsjbRXksQKHQsOy4SL8a49VlkZPr9c6VYUnXTSSSednCj38IrCBtz9x+c+w0ge8p1rX+RTt59oMU4iqS3t0TgbRWNFAbCtezY9aIOe2uQpjdKcm7c3WEmte9l4PA3kx0FcsCVGbGRTelGP7d0VVkZzBnHBt64/ZV0DhWbiyKHe9bA0EV8ztAT2gbOFzHTacqcDAmMn1wnjaMY4mlGaiEeyWzzU26E0UeDUAK3ts1PWO2hPDTkVTe2Md8WO7W2DehbsWU/NtKTvHV/ii/mDPNq7bvX8DXdShWAsLRl1alImqh90p+NoGlhP29UKpcvPkKDIZElpInbVkNwkjKNprUdHsFsNKU3EZmxxDjjd/bZaCfsMbVTDMM7F8tJEAbfhbRc31SrKCFajvMV62q5WUEjG0TSwnqaOAQVt1tOOWqEwsW3fpyB1/Ssdo0oK65I7deP05U2PMN/2OJq1WE+7ahiOYZP1lJs06LubrKeb1SoX021H9lX1uXBYlSbraVcNiYRmPTogQge+kkeGjOUs2BGa5Z7dNXVt2Jm+XeX4cpsiVobxA6G+b7vJdPLcLs+AmpiEbbUS7jdff2KS4Eo7jmakxnrezXSPbbVC4o6Jd6XNRcVNtRrqZ6Jkpnvs68yiY1BhledtNONoSoRhM5oEqu0NNSJ1XntgV1yzBuvq7Nld3r/2Jec6bK/1y+W6TfRFya7uhxS6TW8+329/j1jsiGKmJdvuntiIDgKeZFf32VYrZKLkglsBTHSGQrBVjV35baTQFDrlcnmabx1bX6ahnPMz0+8glhoDrCQF284VfNTPw+eXK8I0M+rcQzJ47AHzwX/x7fy107/rXM4kP3XtL3LjcMSk6HHoAFzXX7DArXe85Xn++MmHedcTFpn83N4af+mhz/OHuzW01iN+t6arPLhi1TTb+ZDN/gH7RYbSkkJHXFyxhrFb+UowbO3O+wySgkdXtvnBjf+PkXsJTHRKJipy034nK2R4WDZjA1pZ4ZrjbbiFHlenXb8kNxEjUdbo9YVI3dxEQcXQ/K0Z/ZzrJLh7Lo3upa3C8Ns31WbL2l32e60y8hHz7XEuRv82X3LNffi2m9HgQMu9dbGt0GaIaZgvrWePSRoM41BHU4c+3MH5WdymeQyasgh6bEaHN+tOjQXk2TbqiG3/m3+4QX1cF6Obl11Xy46x33ZZ/WZ5s/1FxldTLdn8v+xYLKqmFqWpXmqeS+8622Q9NdsF667qpTQ2p/2iC/PUxPz3l/4yozTn71z8NTKhSDBooDCSuYkCyr+OZBetvvn77JRLHjV2z4fSyKDuAlquvD2hmJm41Z+BqCiRJO4cz0wcynx/f+K5/5BY2hiwtfQw7GdWpaylh3z0G3/+s8aYdx85kCdIp3rqpJNOOunkRLmnVU9SuLe3Uxv52UEkDNPDHoNTBxav69kwjgclhSFLKovErlJGSc5aesgoydFGcC7bpycrruWrvGfjMom0bJ0D1SMRilvFCo8Pt5j0MwayYLscWtUOkqcnm5TrMaVxuZeRDWNvfCTYyhrTo7DkbzFpPBtnYSbm3emk49LULB5CtK7/XArZCkTyqrfSSHI3W/H99NsUJgqBdiVRmJmXENpuRZ82iKVejefZUIvRqjUdtj6Pi6wn/93zmxb3qTybyLGTjmvbj0VzdGUSIqvd7Nwf66CCXFiFKHSLCNtMYmRD9ZozU88RWr7SiIRupc71/ZPoFmfKXhPuvLm92Ihlmwse0d6nN+Q3WU/KcY0SoYiMD3hz15UR4RxpI1v03fp8iro+zb5F4Zo5rjz1TCvXj8i0Z/Re7RsZ+3uzvj0uprXK8PeKbyMwmpwTROi7i4Retmbzbfh2g/HaCArHnaKxCkHYVdU3nX421PXpWf2K3PLLRPjcYlo5GoC/Z7VbWdjxy7ASSlr3uO2LXLKSmrt9ekO4QjA3ke07hkgo3r32XGirNFHodyIUB6qOvn850q0oOumkk046OVHu6RUFwL+bPUbkZntACECLY0USKaQjPmojEbHXn2oSqRlFOYlUpJHig2d+N8xMvTGqOBWF2VImKiY6s0ZSomBfCHprP2MYe/6OZQStyjzo3RUSZWyAzVjOUFimvtcdW3dMW98jNHb1wPJuIMz6/KzWBkcVFCYNiYkyWeeCsGz+KMy2raHYpi7NTewMbyrgNjyB08+uU+ysqLmKse1WocyynmrDXbNugmqxnjzDJxMlKbU+27czxOu120yixX362bhN/Slbbfh9hpwFphe2D/pjI8PxUtSJh/wqyp+LSNjVxszNwurjWqGpx5lh++EDwGyAlGgxnQoTkeuESBgynGtrw6HAjycSRTgHXm+fiZJUWFRI5JIJDQM+pUIZa7fw6JEm68liS+oVX0HUSmKViRLc9eHLwSJKfHCd5275tpvMqCa7yR+j0I50eT4aZT6R1mIbGgly3qq/yHoqTRS4W0M5D/2W2DwTPk+HDDP7uF7NoIMBujRx0DKkLimSvxel0AypESfW3VbzH6z+kbNN6ODi6lcUqc//4Ui1ujGD9+1EjrKbOxdtZURY1Vupgn2kcNf0zLnzBgwIwqUurl34m+llvU3m+1f/gKZ4+0UmFDsq46d4+fKKXxRCiIvAL2CTFxngI8aYnxVC/F3gPwd8Iui/bYz5uNvmw8APAwr4L40xv+HKPwD8LBAB/8wY8w/uoAdoI/jEja+1qqSoZC2d4fNob6xYL4coUWAEaVQRxe5m0TGzMuFssscgLjiX7dcMGSHCMjBz6iMpDJk76d441ROKyDFoJCacSCUsHybCMBRl8IeOMGTSqrZyE4cLwEYRlyBg6h7cuIxsQ1GEzGGWF2PVaN5QPjXK+m+bml00FFUwqkVChbEol/s7d4a3npiTmaqhYrEJgHz8RFOyBcaSZz15I6d/KHvuUtPHvz5dNeup2X7aKG8aNRMWeEyNfS4aRRfbbiY08kmUjmM9zYx9UKXCjVO0uU7ek8Y/kGs1Vrt/Yd+icHypBrac5aynFAWCwIzykoj5UtZTJuvYi6bqJZFlq40266ntgJChj2E9QRZVrbonsZ4SlwDJt1FD78rQfh1DogPrqWXoPYb1lKFZjRqJm5qsp6hs9SXB3pOp44IF1a67r3pCheseIBUlUtZMqxoOWJE14kKaxuOBew5kQqOBnrCqoswUlIhwb2VSNSYjIjiRZLIMbfiXTCQMI1EywKsy6zGNG/2z0EkZmFORLFt1B6IikiWJN/wLbDZNf+yA0jh6g4BStpNK3am8mhVFBfxNY8wfCCFGwGeFEJ90v/0jY8w/bFYWQjwB/ADwVuA88CkhxJvdz/8E+AvAC8CnhRAfM8Z88VX0rZNOOumkk9dIXvGLwhhzDbjmPk+EEE8CF07Y5PuAXzbGzIFnhRBPA9/ofnvaZcvD5dP+PuDEF4UxdmYzVzGVltwoVzizeUAsbDKjs6NdCh2TpnVyorRXstab8czeaUa9OZvxPv/1hd+wiGo307lSbpCbJLBhxvIQbQSXqnX++PAh3j24xFgeMnPL14nO+ML8Am/tXQ1qqa3qlFVN6IT16IBxNEMbyY1qxOcPL3I+vR0YO6WJeaYa81xxmieyqyAPg0H4mWqTXTXkQrJDKlUw7m6Vp7hRrfLG9DqRPEQh2FYjcp0y0RmPJLeI5CEFkp1qhcvFaTJZ8mh6w3FwYraqU2xVYx5JbrZyZm9Vp7hWrgUek1cXXSk3mOkeF9Ntl+ozYqsas1PZXNWP9bYCY+dmtcpOtcKjvRst1tOL1Ro71Qpv6m21WE8vVmvsqgFP9K7afNwu57FnEr0xvcFAzgPryaoUJA85NpDv954ahvgCz3q6Wq6xo4Y8mt4MDK9cpzxXnCbXCQ+m26xGuc1FLSJeKDYCj6nJetpTfSSGR3uuL4715HlRkVPB5I71NNcJD6W3GAY3acuRsm3bY+5ZT88VpwF4OL3l2s64Wa2yVw0YRHMuJjuW+aNTLpVnyU3Mo+nNFuvpSrmBNjLEvwAUOuJyuUmEDtwlf0wsOlyG6zY3CZdLe0wGcs65eC+wnq6UGyikTX3qVEeeAeXb9mqWXGWB0+TZTblJuFxsujiXnHPxbmA6+TYSUQUG1FT3uFJukIiKh5KdFuvpqfk5AB7vXasx8ELzxfwC42hm++2uw8vFJntqwKO9G4FovOsYUD6e4WKyHVhPn8svsh4f8FBsszA3WU+rUc6jyS0SNLlTG32hOB+4WCmaiU55vlpnVw05F+9yLt4L5V8qHmAkc4YuVe6Qil0T88X5BdajA87Fe0F1tKNSvjQ/z2a8z4V4lwjDjoujeKo4x2a8z7lon0To0L/SxDyS3uR8NCEShpmO+Up5JuSn34ymDFBMdO2K/3LkNTFmCyEeAd4F/J4r+jEhxJ8IIT4qhFhzZReAK43NXnBlx5V30kknnXTyOpBXHXAnhFgB/m/gJ40xvyKEOAvcwtot/j7wgDHmg0KIfwz8e2PM/+a2+zngE66ZDxhjfsSV/6fAe4wxP7ZkXx8CPgSQbJ76+h/5xPfyJzvn6cclX7n0AP/R132Wm8UKV6dj3jq+xo35iEu7GwC8ee0mX945w7edf4orh2uspzO+f/3TvCXZY+ZmCPYNHXPKRTyXLf29fUv3vGHN6Q0jTNA5znRM4cp9QEzZeBd741gidAiqAYLLqndj9Xr2xeCrpt4U6uCcEKjWcAjUCCQmuNH5cfhyX8cHA3mXvqZtockN8ikppyYNxu+gI28YG3NjZ6TeVXPRVrGYdtPXqY9P1Epn2Ry3t18ssp58u74PiwFTfiXmDdneBlEfKxncW5surc06i/kooA6GawbxHXfOfF+a5eHYLnHk9EmWmmNZbKM+/lX4bfGcedvZ4j69EdTbyhYDD2sbRX0ujusHEFxO/XV73D592WL5Yv1mbofmf6iTkzWD6vz2nvXUlMX7remK6llPzf9Q31tZY/zeDpAJa2TVQGm8y629r30gXtNO0dxfgiE3knTRdXrhWbN4XBaPu28/cgbwZCEOUYb6UALKOBuFgTc9tPWyA+5eldeTECIB/hXwz40xvwJgjLne+P2fAr/mvl4FLjY2f9CVcUJ5S4wxHwE+ArDy5nNGCs20SDjdP2Dt7D6x1CRCs9ab8Z2nvsAvbL2PtewQjaAyktUs5xtWLvENVlvCVPf4cnmKzCVEKY3k+WqNSGg2pDVsjaQ15F2vBjxTnOGx3hZjmVMaG59wQ62Qm4Qz0cTGHTjMtkQzMz3GchaS6uzqAVvVKUYyZyM6cF47gl01YKp7oQwgR7KrBsx0j/XoIHhPlSbmpknY1xnn4r2A2dhVg/DAGslDhq7ticrY1xmARQ34feo+E90P2ASveproPhOdsRnvW9UY9qL0WA6/dPbYDJ+d7UJy26IdTMqNchRUZh5lUJqIbbXCTPdC23acddub0T6ZLIPHzw01CuUet7xbDcNDbD06CAgP38ZIHgYDeW6S+tjGBy2Ex41qNWBDPMKjcPgNbQSb8cQhPFK21Up4yKzHB6HtHd/v2OKkM1kyNVEo93WBMH5tpN1nA+Fxs1olQrMeHwQV064ahJfmRmOfu2pAYeKQgc8jPLadCnAjPggR2rnKAn7CX1szEwc0ykz3eCS5FRAevjzCBNzENIzfHm+vevLj8W17J4zSRNysVkmECkiSiUkCBiQVqoXq8HXrdtpoj/XogNQ4tZZOuKFGAAEnPnHIjK1qHNAeHuGxrVaYuPtkLGcBA+Kz4UVCsxlNgurpplolEVWAUXovpa3qFKlQnI/3nOrJTgC3qpHr9zREcO+4Y+ixIbbtOLRhk1LlaKxH4pZaJUGFNqQw7Ck7zqGcM5aHIerbZ3IEQvlER9xUI5t4Ss4ZyzmZUEx0wrYeBA+zsZwzQLHzp616EkII4OeAJ40xP90of6BR7S8Dn3efPwb8gBCiJ4R4A/AY8PvAp4HHhBBvEEKkWIP3x15pvzrppJNOOnlt5RWrnoQQ3wz8O+BzENbOfxv4QeCdWNXTZeCvOcM3QoifAD6I9Zj6cWPMJ1z59wA/g10pfdQY85Mvtf+1x8+YD/7yt/Enty/w2OpNnp+t8U1rz/LCfA1lBD9x7pP8wxvfblMDAqeSQ3aKAf/d+U+ENmzEK4HZArSWis1lYHCBEyqompQRgfPil6xzp8LJTRzSMy6TxSVls3yRe7OoahnIo+wdLxalXC+XJYaSo8vxqYlbaptmZGuTl7SoxlnWf68+akXHLlk2v5T43MLNOICmvFQ/FvvejDb3aqdm2tNmG8sYS4tqppI64valxnYc7+k4xlP4/QR11GI7TRVTu4363C3+triv48axqNJbPBfHcaJO2t9x+3k5rCc4es5PYj1lToUHhDovh/XkU6X6/YB1jy3N0eeGV/U2XWOhVm/5/Xk1FbTdYo+TuYla3KfegmoWCKqs3EQMhCI3kkxoItdX3++5gTf/aaqejDH/Dyy9yj5+wjY/CRx5Cbg4i2O366STTjrp5O7JPRuZ3Y8KzqT7fMvmIQNZsJEe8GC6zcO9WwHn/O6VZ5k4rK42kkcyEd7g3sicoIlE/cb30ZZhVuGCVTxjxc/QMXamUWBThfpIyVaktqZlfG3OuKE9W/P7lN4w52fBjahSH5ktTW1E9m37gKXcJETMW0ynwIGhZj3lJgk68KzBYgJaUcp+7tI0Ti9jNyXUPKZFHo+vv1hOo+2meHaXj7ZfDLDz66llbYMzTnt+0RLWU0lUt+101c0VB9RMq2Y/fH2cYXuR6eRXIcodl7RpCPbHylgW0zI2VCKqwG8qTEKTFJugLHfLnSMbrOeDtRrlQoX+FERgak5Tbaiuj0eKOpn1ZGrWlz/ezfJm3WXly/bZLC9NbI+bkSRUrfr+uod6FeH5UM1+l84wb9v2rKb6CDcjm30b4XwKTz2wgbASHSKtAUpxlMdUGkPpDNhN5xQ7ntopJawaXN3mOKRbdfhyv5LxdRYdXUp3jeeNlUmzrl6Ys9tnVNuBRjvHm1ci9+yL4lR0yPeufC5gdmcmZiwLEmENLxHw/sHlUF9jLf8ztzTzhip7AmhcoBYyGC4WQXgh7KgVLjq/Zu8VATi4XkmOfZh61Id/4EdCNS6kONxwkhrLYSOMK3AvAI8aUFgERoKPDC/DzSJbN5zHbqjwQvNwMXsz2QxhvryO8G17JRUB6Ff3D/yDzmE9wsPMPdBpqw2UkZREAQ+BQ3j48WSi9gXTjQeuN7yBfeE0USL+hVQ0bvLUnx8jW2olhO27QoSXwiLCwxvMM1kGJIhu7DO8QExd5utH7oVw3Is/wO4wLVVTaWJKaCE8fH3w6qT6JWTHLIlEEV5AzZeTbHhw1WoxexR8f4OaRkCECi9Vn3dFCR0mJU04pa1vX8Iev5GGdhZezoLWefP4jcV92v6ZVnlhIiJ3Tprwx9K94P2D34/H404i1++pSRmJvH6Zi6o+900IZ/CYar8QswDvtPDDyAhS9+CP3L1S56qp3KSSgODw8D7b9lEooPfYWlTL4oCguXseZKjWPpvltbpKkUDYZ7OuR4BkQqGxE+ASiTb2mpdGQGNC/HKlgwJ20kknnXRyotyziYve+vbUfOz/2iA3kqHUTLVkLDWJEHaGEgxh3ufazgR2NQz87MK1VRpaS7I0zJhlKw5hohPWZUHeMGY3/090Et7+WWPJvLiMhHr2cZLf/TLxKq7F+i3/+gXjGdRGs+aMwvfNz2x8O8v85Y/wlRpykvF5cXyLY1wWF7DMIDpzwLuX6ssy47avVyysAKCOgQh9aMWiSBaNyov1l+2z9Zs3oC4Z07Jj48WzpRbjOvz3ZoxKHYfSTli0GHNyJ/ttjmnZuVg0Wi+ynu5kn8tiA5aVLYs7WayXm5ixnB9R7fg2ekIFNbOPsWjeh7XzQNvpw7fjGUv2c8168hqKJutJYsJqpHm/NRMTpc7VdVFVvWjUbjrR+GfMYnnze4v11BDLeiL0+5XGUXQrik466aSTTk6Ue9ZGMTcxExOTYFcTGsHECD59+BDfkD3PyL1pr2trcLpcbfBYcpNEaOYGbqo+W+oUhYl4c3Ij6BK31Cpb1SkeTW/gA1UUgq1qxI5a4dH0hkUTOyPRdjXkxWqNx9Itl/LU5kbOXTDRheQ269FBYD1tVWM8H2coCnaNzT18tbRteMJogQ1c2qpO8cb0BmM5czpUzU21yna1whvTG4xcIN6OC/zbVQPbjigD6+lGNSISxnKdXPlNNeJKscGj6Y0W6+mmWuVmNeLR9IZlPTn98efzi/RkGbhLPrCqMBEz3bPHxdlifL992SKP6eH0Zov1dKk4w61qxDcOnjnCesp1wiPpLRJRMTUpW9U46NI9G8i3PdF9LibbgYLb5BqdT263WE+ex+T5Sl6f/WK5hjaSB9PtFutpplMSoTif3A6spxfLNWaqx8O9WzRZTy+Wa+Q64eHerbAKmuiEF8uxa3unxXq6Uq4TYVpt71QrztZVcT65bevrHlvVqdBvz3oqTcqVwhIILqaWISaFJlcZL1aWoBxSDyUAABDISURBVNPkLm1VY3KdkEmbe9mXP1+uU5qYTJaci3etrUynob4/tp711Gy7yXrynCZ/fvx58AGbPsixyXSKhAkMqKnu8WK1RiIUF+LbLdbT5WKTSOgQKJibhG0teWp+jlF0GALx/LWijGAczTjjgugmbpypsLnczzumW2kinirOMZI5F+LbIZXASaynr5RnQl5rH+l+tVpjqtPAnfJI/2fKMwzlnIGYM45mgfV0qTjDQM5DbmwbRJdyudxkHE05F+2TYRlNCtEqT4RmT1lG14vlGu/oP9diPV2uNhiIOalQbEZTJIqb+pUlLrpnVU9vf3tiPvWJTWaN/o+EX/4KtDHhM+CMOobcGCIgEgJlDD4Uf6q9isCEZVy5sIy1EZd1CP7icrjpP+2XmxOTBDXU4lJaG8HUJAEb3lRHHaeWspgAj45oZK5bqNtcCvttm0tkj0i/U4SHcsZwP9a2yqPt1dVURS3LobyI8MhNYvMAiOJYhMdxqo2XQnh4CbkJGgbgRZw4nIzw8O14ea0RHs1+3CnCw5a11UCLCA+/v+Zvx/WlWXexzWX9aDqB+O8noTqOKw/3EMcjPOyY6s8t9VC4LhvxC86469VSy7LJgfV09Pfo4n37ahAeHve/DOERiaOqNahVTcvUd0eOVaNu4VTwYeyh/muD8OhUT5100kknnZwo96zq6dDEXFfOh9nNInJh2FJDzkXToHraVZISyY4acjY6IBOGObCrErbVEIAz0UGYqdyoVpiZHpvRPhEmsJ5uqiHbasUteVWYjW+rIRPd51y8y0gWQfVUEoUMd171tKsHIcbD845yk7BdrjDR/cA08qqnHbXCvrKsmpr1ZNjWQ6a612I9ecbMVPe4EN8OTKcXVT/EkpyL9sKq4GY1Yl9njOWspXraUSvs6z4Xkp3QNsBT83NOJbFXs5uqlWAk9lhqXz5RfTbjfVKhalVVuWr7ney2WE/PFGc5UBlfm10J6huAG2pErpMjbdsViQxsqGbbfp9eLXGjGjHTPc4le8H9cqL63KxGgdM0kHM862mnWrFtO/VI6dhIc21XPRvRQVAP3Qy8qElQPU1NxPVyjMLxojy7yyTcdGygzXjSUj3drFbDNeHVYH6fiag4l+wFlYxnQPnx+PiKZhtN1tOO4zH58cxMHBhaiahazKSt6hQ+U5/nN3kVoz/eTdaTV6Nuxvu16klbZpIv9237NjJRtphOvg0pNGeiyREG1Ga8T2R8dri6j02V2VRoXizXyGTJWM7qc69GRBgyWQR2W+44Uj6W5UK8i0Kw69RgHrFu45EMM51wtVojkwUX493AepqbiKvqFBGGzWiCZz3ddMc2E6VDm1vWk1WlWfz9QM6D6unFas1hwCdhFbWnErbUKQZizkY0JRMqkBSa5V71tK2HbJVjHuttcS7y44zYqkYhHmpDHt4d1lMnnXTSSSd/NuSetlF84uOnyRvdH0nhgk1q91gvXntXNMbry3LTdme7U9aTx443XeBskMtRJPKiHOdSeZKNAuognpNk0VXWj2tRfMCQ/VwHCRXUucLvxJWyaR9obrM4lmVjPsk9tukSe5ws2lFeivXkZZmba+jHgu3Bl2nkiWNZ2r8F991FN9njju9xrKfm9stcl235nbOeYLnr6VeD9bRM7+4JAx5T3qx7kktts9+J0MG+t7i/RQR5sx9QI8h9gJr/3W9zHOupaZ9YtP01vzf/+/29XNZT0z12mfhgY9u+tUc03WRfC9ZTt6LopJNOOunkRLlnbRQWz0Br3pUbQ2kgE4bIeTv5FUTZeMuqJeTH0KazPYRZe4P11EwAj5tN+PIUHWY2nhmzmGindLwoaM/2mvwaILBqcmosg2c94VY0y1hPflaXieqId4jC8m58ebGAVfA8nxwR9NeJUDRZT1BjNlpYBmNsgBieN1WjIPw4FQTbg9dz27412sa17b77FLXL9un70mzD79OznpoYlMXZae50tdY108/ujrKePDaj6SmFC4bzOIk0eMzoFgakifCw7dhZcypUWDGUDs1RH5fK9SNpjLO2RQSchlCogBmp2VWWF+XHCdrVbyJMmgwtz0zySae8BI5W4xgmwXtvyT79sV0obzGdGl5avjw3CQnqCOspdyvD5n3SxN1komwRi6cmbdXXRjIlIqMM94r3kssb96BHX8xNxNTZJZrJnEohyQPWxXsLWtaTzRFRaw8UgrmuVzZNHpNvI0PZbdwqIw/3Vb0K9J6IodzooKkIXo4Nyu3UpCTOjiNRbrVzVEvyalhP9/SKQrl73x9s7f4WIby+3ItPGKMRlNRQr0VXv6baqOmK6aXOnNVGVvuyZb/Z/+12Jrrf5vI0+77kxAZVSuMF13Rpbbaz2J+mLPYDanjdkf15ntJiJLSp4YXNsuNkUeXTbHtRmmon/xDz9RbrqyXH+aX6Y6+BdnvKSPZVtrT9lsqkqdYyR8e07Lwt1m+61S5VrSw798gjx3DZOWuO8Ti1TfMa9fXuWKWGXFr/+HJx7HFZvDZr4OTyuov9b95XzXuiWR9ovQibdRY/t/d39L5v/tZWo4nWcfTPj2Ybi8+Uk87b4r6WbaONYCiKpao3vXAsmmUvV+7pF0UnnXTSSSdffbmnjdm/+YlNcmOYahtskrkgukxIFIaoNWMwTt1kmBnBwFEgPQslb6ihPIelyXo6LnHRojSN2X4Z6eU41tPUJAzd7PmlZnTNJepiANQyA3gzuO5IXxszuZdiPdn+66Wzq8VgNy+v1pjtxaeA9C61xwUF+u9NaeLQ78SY7VPYDsT8iDF7cbs7MWy/UtZTMwBwMUhwcfvFwLvm73diXG6Ox8sy4/Ri7vOmvFJjti9fVnYnrCfgjo3ZuzpjVcxZxnpq9utOjdnLWE9fjcRFL2XMtn3Trv22mv2+Yz0JIT4ghPiyEOJpIcTfutv96aSTTjrpxMrrwpgthIiAfwL8BeAF4NNCiI8ZY7543DYlktwYBkKQRQYQLdfXkUxRxjAzdqY+c3UjYF1Cbqxb7K5O2ZRzRtKSISc6IjcRQ1GRCs3AhevvGRnSDA6lnVeWGGbG1h/JkkwYSqOZmMQatbHteMTATMc1Z14oBqJCuZmQX1UMHPemNJKpiSlNZMtlFWYiMx2TEzESZSBaTpzRMidiLAsyYUL+jbm2RnTfR2VgYmxfMlHREzXzfmpSShMxknkrgcu+6bFbjbgQ74aAw6lJUEgiIxiKkkxaQ92+6bl+FyRCMXAzvmZ50+C+b3poIxmLQ6SsLUyWbyMZioJNOQ3Ik8LpmoeiaLXdNHJmwiavz3WCMjaPxFAUwZ6yqwZoJCN56HKH2JXHvs5IREUqFImwwW9Tk9b7lPMQ0FXoHiWSgZi3AtEmuo8ytu2hc1ssXLm9Ng8t08qtdFrlLsgvN4nL1aDduVAUwnK17Lm0ZX6fU5NSYs+bn/n642WPVRlIqhNnyNcYBrIMrqF5IxhrKMrGNWHP86qYA7TKQ11pDdrN8pEsSNDBUFxiZ+t+n3MTsW96IYfKSBZhFT41CYlQDF0OFX9P+D42+52g2TM9h4GpSByhdaYTFMrts2JTztAIpo3V89DlsMmNYKrTUAZ2Fu3vLSkMPQFpw0lmaixjbiBUSDmamyg4w9i+2HJ/f0qMu/ftM2hmYhKhQxsS68LqSdQDocgEzNwqZ6bjkHo5FTqMxeaYUURAJgW505z4FdNAQCYkk2Pcrl9KXheqJyHEe4G/a4z5i+77hwGMMf/Tcdu84+2J+e1PnGmVJUKSiAh5zEKpNIoDUzIQLhEJhplWJMJGPNuy+mJQZnFpDpmrGwn7Yopcuf/vl6RND6tlctzpWlTXLP6WYI6ghBfFX+A+gZPvO41yqJek3tvLbrs8x7bEhCRRtp06dsSr55apt46TlvdXY1+LS/imLCKbfZnvX5N9dZyRcZnqbPFYL1Ox+bIT1UyNGA7/fVG895b/7I/BYj+OU+E0+9nu89FyfxxDfxpxQb7escbUY7DWYduFWJ7F+sv22Yp3aeCzU6Fb6txFDpK/nlvtNvptJ2h1efP+aaqJdKM9L0ljWM3f/eeE+t7JhFdBRZRGozDhuVG6uosMucU20sZzw9dtj6u+Z0+SmanHOhCQeKYdNo4Mas5dabxaSlIazdkHr92zqqcLwJXG9xdcWSeddNJJJ3dZXheqpzsVIcSHgA+5r/PTD774+bvZn6+ynAZu3e1OfJXkfh4bdOO71+V+H99bXu4Gr5cXxVXgYuP7g66sJcaYjwAfARBCfOblLp/uJbmfx3c/jw268d3r8mdhfC93m9eL6unTwGNCiDcIIVLgB4CP3eU+ddJJJ510wutkRWGMqYQQPwb8BtaW81FjzBfucrc66aSTTjrhdfKiADDGfBz4+MvY5CNfrb68TuR+Ht/9PDboxnevSze+BXlduMd20kknnXTy+pXXi42ik0466aST16nccy+K+w31IYT4qBDihhDi842ydSHEJ4UQT7n/a3ezj69GhBAXhRC/I4T4ohDiC0KIv+HK74sxCiEyIcTvCyH+2I3vf3DlbxBC/J67Tv+Fc9K4J0UIEQkh/lAI8Wvu+/00tstCiM8JIf7IewPdL9cmgBBiLIT4l0KILwkhnhRCvPeVjO+eelE0UB/fDTwB/KAQ4om726tXLf8r8IGFsr8F/JYx5jHgt9z3e1Uq4G8aY54Avgn4UXfO7pcxzoH3G2PeAbwT+IAQ4puAnwL+kTHmTcBt4IfvYh9frfwN4MnG9/tpbADfbox5Z8Ml9n65NgF+Fvh1Y8zjwDuw5/Hlj88Yc8/8Ae8FfqPx/cPAh+92v16DcT0CfL7x/cvAA+7zA8CX73YfX8Ox/hss0+u+GyMwAP4AeA82YCt25a3r9l76w8Y0/RbwfuDXsGmR7ouxuf5fBk4vlN0X1yZwCngWZ4t+NeO7p1YU/NlBfZw1xlxzn7eAs3ezM6+VCCEeAd4F/B730RidauaPgBvAJ4FngF1jjE/9di9fpz8D/LfU6KIN7p+xARjgN4UQn3XkB7h/rs03ADeB/8WpDv+ZEGLIKxjfvfai+DMnxr7273nXNCHECvCvgB83xuw3f7vXx2iMUcaYd2Jn398IPH6Xu/SaiBDie4EbxpjP3u2+fBXlm40xX4dVZ/+oEOLPN3+8x6/NGPg64H82xrwLmLKgZrrT8d1rL4o7Qn3cB3JdCPEAgPt/4y7351WJECLBviT+uTHmV1zxfTVGAGPMLvA7WHXMWAjh45Tu1ev0zwF/SQhxGfhlrPrpZ7k/xgaAMeaq+38D+FXsi/5+uTZfAF4wxvye+/4vsS+Olz2+e+1F8WcF9fEx4Ifc5x/C6vXvSRFCCODngCeNMT/d+Om+GKMQYlMIMXaf+1j7y5PYF8ZfcdXuyfEZYz5sjHnQGPMI9l77bWPMf8J9MDYAIcRQCDHyn4HvAj7PfXJtGmO2gCtCCA8B/A7gi7yS8d1tg8srMNB8D/AVrB74J+52f16D8fwScA2LtH8B60GygTUgPgV8Cli/2/18FeP7ZuzS9k+AP3J/33O/jBF4O/CHbnyfB/6OK38U+H3gaeD/BHp3u6+vcpzfBvza/TQ2N44/dn9f8M+T++XadGN5J/AZd33+a2DtlYyvi8zupJNOOunkRLnXVE+ddNJJJ538KUv3ouikk0466eRE6V4UnXTSSSednCjdi6KTTjrppJMTpXtRdNJJJ510cqJ0L4pOOumkk05OlO5F0UknnXTSyYnSvSg66aSTTjo5Uf5/6jkOd0omX9AAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<matplotlib.figure.Figure at 0x7f88cd1269e8>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "plotSpectrogram()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Thanks for reading !"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.5.2"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}

Credits

Sam

1 project • 2 followers

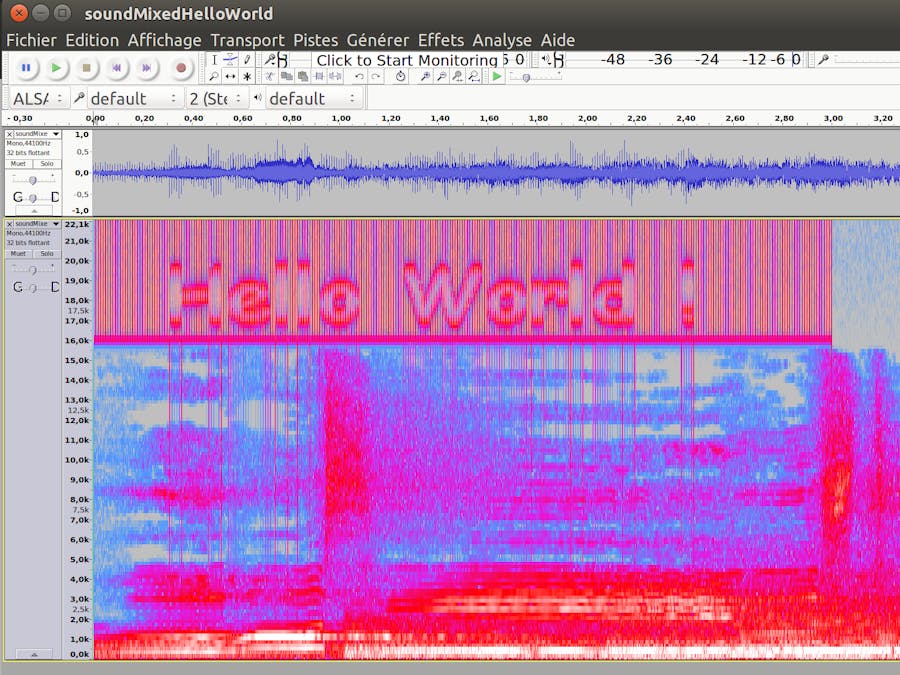
Encode Image In Sound With Python

Things used in this project

Software apps and online services

Story

What?

How?

How to do it?

End result

Code

Code that actually works

Detailed explanation of the code

Full Jupyter notebook

Github Repo

Credits

Sam

Comments

Embed the widget on your own site

Encode Image In Sound With Python

Encode Image In Sound With Python

Things used in this project

Software apps and online services

Story

What?

How?

How to do it?

End result

Code

Code that actually works

Detailed explanation of the code

Full Jupyter notebook

Github Repo

Credits

Sam

Comments

Related channels and tags