Intelligent Drowsiness Monitor for Safer Driving Through CV

Introduction:

Sleeping, one of the most basic needs of the human being, is a daily task that, at least, we must perform for 8 hours. However, it seems that sleeping is a luxury that not many can have. Some do not sleep for pending work, for enjoying some more episodes of their favorite series, or even for a party.

Not sleeping today is a common practice among young people, however not sleeping reduces the ability to react and attention to perform tasks as simple as sending a text message or even tasks as complex as driving a car.

According to the National Highway Traffic Safety Administration and the Centers for Disease Control and Prevention they say that it is 7 times dangerous driving tired to driving drunk.

• Number of drunk driving crashes: 10, 874 *
• Number of tired driving crashes: 72, 000 **

The problem we have here is, what happens if we need to drive and we are tired?

The best solution to this problem will always be to sleep at night, if it is not possible to do it, as a solution I create the drowsiness monitor to avoid falling asleep while driving.

https://www.nhtsa.gov/risky-driving/drunk-driving *https://www.cdc.gov/features/dsdrowsydriving/index.html **

Connection Diagram:

This is the connection diagram of the system:

VMA Circuit for RaspberryPi:

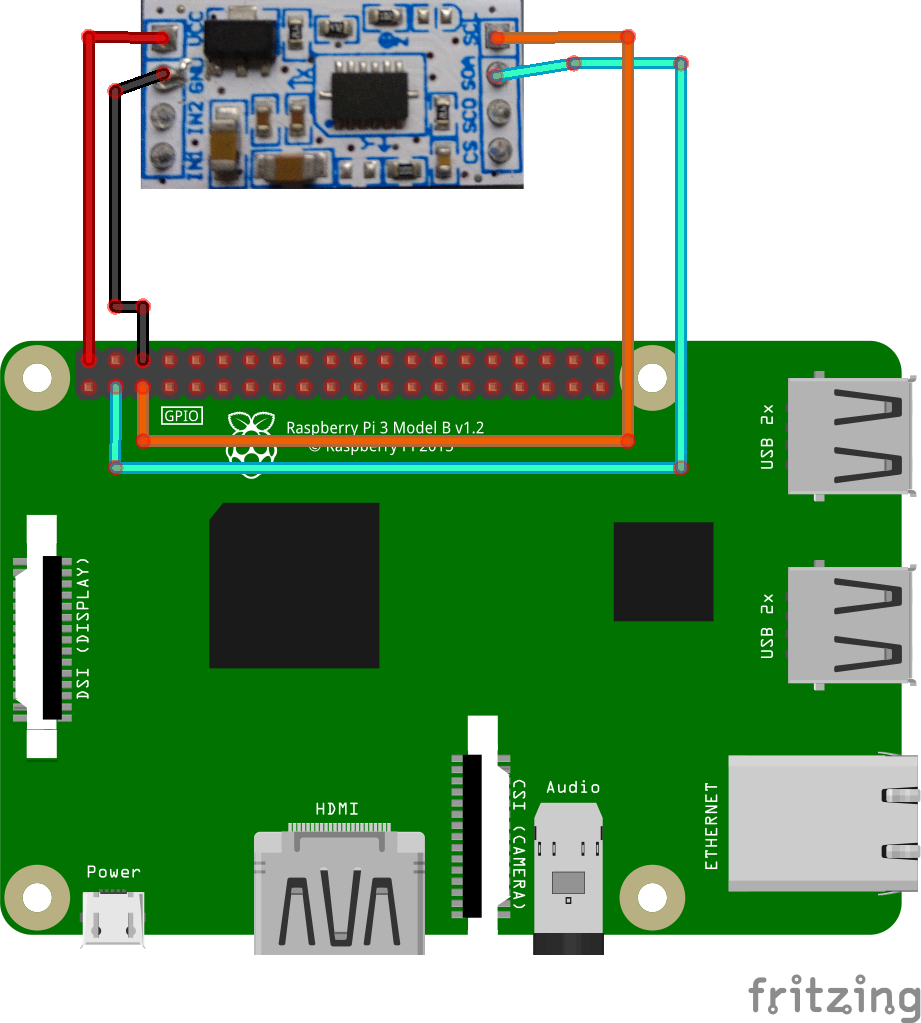
As a first step it is necessary to make a circuit that allows the Raspberry to obtain the accelerometer data, communicated by I2C also known as TWI, it will be necessary to realize a circuit which allows the connection of this module to the headers of the raspberry.

This is the connection diagram:

In my case I made a "Shield" with a PCB Breadboard so I could place it on the raspberry easily.

Already placed on the raspberry:

Otherwise, if you do not want to make this "Shield" you can simply connect it using dupont cable XP, but the soldered circuit is always better.

Raspberry Setup:

Note: for this tutorial it is necessary setup the raspberry with an HDMI monitor and a Touchpad and a Keyboard USB. We will not use a normal internet connection, we use a connection through the Huawei 3G USB dongle.

• Download "Raspbian Stretch with desktop" from https://www.raspberrypi.org/downloads/raspbian/.
• Flash Raspbian on the sd card as indicated on the official page. https://www.raspberrypi.org/documentation/installation/installing-images/README.md
• Connect the RaspberryPi 3 HDMI cable, connect the other side of the cable to the screen.
• Connect the SD card to the raspberry.
• Connect the USB of the Touchpad and Keyboard to the raspberry.
• Comes the Huawei 3G USB dongle to the raspberry.
• Connect the speaker to the jack output of the raspberry.
• In this case connect the USB cable to the battery and the microUSB to the Raspberry for powered.
• Once you achieve this you should see Raspbian's desktop on the screen.

OpenCV Setup:

• As a first step to configure raspberry correctly we will have to connect to a Wifi network, because we will have to install OpenCV in the raspberry.
• https://www.pyimagesearch.com/2018/09/26/install-opencv-4-on-your-raspberry-pi/

This was the tutorial that I used and it worked, however there are many different tutorials on internet, if this does not work try another one.

• https://www.learnopencv.com/tag/raspberry-pi/
• https://tutorials-raspberrypi.com/installing-opencv-on-the-raspberry-pi/
• After performing the tutorial, we will put the following command in the terminal.

pip install smbus pygame time

• With this command we will have all the libraries installed.

Example of image processing with OpenCV: Click on the image

Webcam Setup:

• To install the webcam correctly we will use the following Raspberry official guide.

https://www.raspberrypi.org/documentation/usage/webcams/

• As a last step we disconnected the internet raspberry to stay only with the connection that the Soracom Dongle will give us.

Dongle Setup:

• To configure the Dongle, we will use the official Soracom guide to correctly configure the dongle in the raspberry.

https://github.com/soracom/handson/wiki/1.3.-USB-Dongle-configuration-tutorial

Raspberry Software Development:

Open in Thonny Editor this code and run.

# -*- coding: utf-8 -*-
   """
   Created on Thu Apr 11 01:48:57 2019
   @author: ANDRE
   """
   import smbus
   import numpy as np
   import urllib.request
   import cv2
   import pygame
   import time
   import os
   import math
   import requests
   import json
   # Code to create the Accelerometer Module and obtain data from its.
   class MMA7455():
       bus = smbus.SMBus(1)
       def __init__(self):
           self.bus.write_byte_data(0x1D, 0x16, 0x55) # Setup the Mode
           self.bus.write_byte_data(0x1D, 0x10, 0) # Calibrate
           self.bus.write_byte_data(0x1D, 0x11, 0) # Calibrate
           self.bus.write_byte_data(0x1D, 0x12, 0) # Calibrate
           self.bus.write_byte_data(0x1D, 0x13, 0) # Calibrate
           self.bus.write_byte_data(0x1D, 0x14, 0) # Calibrate
           self.bus.write_byte_data(0x1D, 0x15, 0) # Calibrate
       def getValueX(self):
           return self.bus.read_byte_data(0x1D, 0x06)
       def getValueY(self):
           return self.bus.read_byte_data(0x1D, 0x07)
       def getValueZ(self):
           return self.bus.read_byte_data(0x1D, 0x08)
   #Audio File attached in the repository or hackster page
   file = 'b.mp3'  
   #Initialization of pygame to play audio.
   pygame.init()
   pygame.mixer.init()
   # The haarcascades are attached in the respository and hackster tutorial.
   face_cascade = cv2.CascadeClassifier('haarcascade/haarcascade_frontalface_default.xml')
   eye_cascade = cv2.CascadeClassifier('haarcascade/haarcascade_eye.xml')
   # Input Camera Source.
   cap = cv2.VideoCapture(0)
   # Url to send data to Soracom and Obtain Location
   url = 'http://funnel.soracom.io'
   send_url = 'http://freegeoip.net/json'
   #Count Variables
   nf=1    #Number of Faces
   ne=1    #Number of Eyes
   count=0 #Special Counter 
   mma = MMA7455()
   # Memory X,Y and Z values to compare
   xmem=mma.getValueX()
   ymem=mma.getValueY()
   zmem=mma.getValueZ()
   #Converting signed byte values to unsigned byte
   if(xmem > 127):
       xmem=xmem-255
   if(ymem > 127):
       ymem=ymem-255
   if(zmem > 127):
       zmem=zmem-255
   # Seed Time values
   time1=time.time()
   time2=time.time()
   while 1:
       x = mma.getValueX()
       y = mma.getValueY()
       z = mma.getValueZ()
       if(x > 127):
          x=x-255
       if(y > 127):
          y=y-255
       if(z > 127):
          z=z-255
       # We need compare the memory value and the actual value to determine the acceleration, if the acceleration is more than 10, we determine the car crash, you can adjust this value for your convenience.
       if(abs(xmem-x)>10):
           print('crash')
           # to obtain our location we send a request to "send_url" url to obtain our position
           r = requests.get(send_url)
           j = json.loads(r.text)
           # We convert json to string
           lat = j['latitude']
           lon = j['longitude']
           # We create the payload and headers
           payload = '{"deviceid" : "Car 0001",    "lat" : lat, "lon" :lon}'
           headers = {'content-type': 'application/json', 'Accept-Charset': 'UTF-8'}
           # We send to soracom the notification
           r = requests.post(url, data=payload, headers=headers)
           exit()
       if(abs(ymem-y)>10):
           print('crash')
           # to obtain our location we send a request to "send_url" url to obtain our position
           r = requests.get(send_url)
           j = json.loads(r.text)
           # We convert json to string
           lat = j['latitude']
           lon = j['longitude']
           # We create the payload and headers
           payload = '{"deviceid" : "Car 0001",    "lat" : lat, "lon" :lon}'
           headers = {'content-type': 'application/json', 'Accept-Charset': 'UTF-8'}
           # We send to soracom the notification
           r = requests.post(url, data=payload, headers=headers)
           exit()
       if(abs(zmem-z)>10):
           print('crash')
           # to obtain our location we send a request to "send_url" url to obtain our position
           r = requests.get(send_url)
           j = json.loads(r.text)
           # We convert json to string
           lat = j['latitude']
           lon = j['longitude']
           # We create the payload and headers
           payload = '{"deviceid" : "Car 0001",    "lat" : lat, "lon" :lon}'
           headers = {'content-type': 'application/json', 'Accept-Charset': 'UTF-8'}
           # We send to soracom the notification
           r = requests.post(url, data=payload, headers=headers)
           exit()
       # We obtain an image from our source of images (in this case the camera)
       ret, img = cap.read ()
       # through the following algorithm we get the number of faces and eyes that the camera can see
       gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
       faces = face_cascade.detectMultiScale(gray, 1.3, 5)
       for (x,y,w,h) in faces:
           cv2.rectangle(img,(x,y),(x+w,y+h),(255,0,0),2)
           roi_gray = gray[y:y+h, x:x+w]
           roi_color = img[y:y+h, x:x+w]
           eyes = eye_cascade.detectMultiScale(roi_gray,1.3, 40)
           ne=len(eyes)
           for (ex,ey,ew,eh) in eyes:
               cv2.rectangle(roi_color,(ex,ey),(ex+ew,ey+eh),(0,255,0),2)
       # Since we have the number of faces we will check that the algorithm can see at least one face and at least one open eye, if it is able to see a face and does not detect any open eye, after 3 seconds it will start to sound an annoying noise that will wake up to the condutor
       nf=len(faces)
       if(nf>0 and ne<1):
          time1=time.time()
          print(time1-time2)
          if((time1-time2)>=3):
              pygame.mixer.music.load(file)
              pygame.mixer.music.play()
       else:
           pygame.mixer.music.stop()
           time1=time.time()
           time2=time1
       cv2.imshow('img',img)
       k = cv2.waitKey(30) & 0xff
       if k == 27:
           break
   cv2.destroyAllWindows()

• Save the file in the Desktop with the name "E.py".

Configure the audio and initialize the code with boot.

• Open terminal and write the next command.sudo nano /etc/rc.local
• Add after "fi" paste the next code to set the jack output and excecute the program.amixer cset numid=3 1sudo python E.py

Cloud Development:

Note: This tutorial is designed for people who already have an account and SIM registered in https://console.soracom.io/

Configuration AWS IAM Credentials.

As a first step we will have to configure AWS IAM so that Soracom can communicate without restrictions to AWS IoT.

• In the AWS console we look for IAM.

* We enter the option of IAM.

* Inside the IAM console we enter the "Users" option.

* Click on the "Add user" button.

* We put the name you want and select the option "Programatic Access".

* In the "Attach existing polices directly" option, we select "AWSIotFullAccess".

* Once we finish everything we will access our Access key ID and Secret Access key (Save them well because we will use them to configure the Soracom console)

* We go to the AWS IoT Console and go to the "Settings" option.

* In the "Settings" option we obtain our Endpoint API.

Configuration Soracom Funnel.

• In the Soracom console we enter the group that is the SIM Card.

* Browse Funnel and paste the Endpoint that we obtained in the AWS IoT console and add the Topic where we will post the data.

* Finally We create the IAM credentials in Funnel as shown in the image.

Configuration AWS SNS.

• We create the topic that we want.

* To subscribe an email or a mobile phone select the option "Create subscription"

* All the notification options we can make are all the following.

Configuration AWS IoT.

• In AWS IoT we will create a rule that allows interacting with other AWS services such as Lambda.
• In AWS IoT Enter the "Act" tab

* Click on "Create"

* We select any name for the rule and we put in Rule Query statement

SELECT * FROM "crash"

* We select the option "Add action"

* We select the option of Send message to lambda.

* We select "Create a new Lambda function"

* We set the Lambda configuration as shown on the screen.

* In the code section we paste the code below, editing the "TopicArn" for the topic created in the previous point of SNS.

• Lambda NodeJS Code:

     console.log ('Loading function');
     // Load the AWS SDK
     var AWS = require ("aws-sdk");
     // Set up the code to call when the Lambda function is invoked
     exports.handler = (event, context, callback) => {
     // Load the message passed into the Lambda function into a JSON object
     var eventText = JSON.parse (JSON.stringify (event, null, 2));
     // Log a message to the console; You can view this text in the Monitoring tab in the Lambda console or in the CloudWatch Logs console
     // Create a string, extracting the click type and serial number from the message sent by the AWS IoT button
     // Write the string to the console
     var latitude = parseInt (eventText.lat)
     var longitude = parseInt (eventText.lon)
     // Create an SNS object
     var sns = new AWS.SNS ();
     console.log ("Received event:" + "https://www.google.com.mx/maps/@" + eventText.lat + "," + eventText.lon);
     var params = {
     Message: ("Your family or your employee has crashed at the following address:" + "https://www.google.com.mx/maps/@"+ eventText.lat +", "+ eventText.lon),
     TopicArn: "arn: aws: sns: ap-northeast-1: XXXXXXXXXXXX: SoracomCar" // Your SNS URL
     };
     sns.publish (params, context.done);
     };

• Once the lambda is created, we return to the tab "Configure Action" to add the lambda to the rule and select the lambda we created.

• After this everything will be working, every time you send data, or if you happen to be in a crash, an SMS will be sent to all recipients subscribed whether it is by emil or cellphone.

The assembly of the product:

• Mount the battery in the case that we will use to power the raspberry.

• Mount the raspberry on the battery.

• We connect our "Shield" of the accelerometer.

• We put our USB cable to microUSB to power the Raspberry.

• We connect our Speaker to the jack output of the raspberry.

• We connect the USB camera to the Raspberry.

• We connect the Raspberry Dongle.

• We close the Case to finish the product.

The Final Product:

Now just put it in your vehicle and you are set! You will not have to worry about falling asleep while driving!

Future Rollout:

During the development of the project, I really enjoyed the Soracom platform as I was sending data to AWS IoT. The next development that can be sought to follow, is to improve the case and the components to obtain the following advantages:

• To Power the RaspberryPi with a feeder in the car.
• Improve the facial and ocular recognition algorithm.
• Improve the case to make an attractive product.